Статья опубликована в рамках: V Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 14 ноября 2011 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Моделирование процесса поиска пути в лабиринте при помощи UML диаграмм и сетей Петри
Марков Александр Владимирович
аспирант по специальности 05.13.01 “Системный анализ, управление и обработка информации (в промышленности)”, НГТУ, г. Новосибирск
E-mail: muviton3@mail.ru
Романников Дмитрий Олегович
аспирант по специальности 05.13.01 “Системный анализ, управление и обработка информации (в промышленности)”, НГТУ, г. Новосибирск
E-mail: dmitry.romannikov@gmail.com
Воевода Александр Александрович
д. т. н., профессор кафедры автоматики, НГТУ, г. Новосибирск
I. Введение
Разработка программного обеспечения включает выделение свойств системы на основе анализа модели предметной области и требований к ПО.
В зависимости от класса создаваемого ПО используют «ручное» проектирование, либо пользуются различными средствами его автоматизации. Описывая характеристики ПО, применяют разнообразные нотации – блок-схемы, ER-диаграммы, UML-диаграммы, DFD-диаграммы, а также сети Петри.
Применение UML диаграмм совместно с сетями Петри [2, 4] предоставляет разработчикам возможность выявить неточности еще при постановки задачи. Анализ динамики функционирования системы можно описать через свободный язык сетей Петри [1].
Сети Петри — математический аппарат для исследования систем. Считается, что анализ сетей содержит важную информацию о структуре и динамическом поведении моделируемой системы.
Обычно системы состоят из отдельных взаимодействующих компонент. В свою очередь любая компонента может быть системой, но ее поведение можно описать независимо от других компонент системы. Исключением являются точно определенные взаимодействия с другими компонентами (совмещённость или параллелизм).
Поскольку компоненты системы взаимодействуют между собой, необходимо установление синхронизации. Обмен информацией от одной компоненты к другой требует, чтобы действия включенных в обмен компонент были во время взаимодействия синхронизированы. Это может привести к тому, что одна компонента будет ждать другую компоненту. Согласование во времени действий различных компонент может быть очень сложным, а получающиеся в результате взаимодействия между компонентами трудны в описании.
Сети Петри разрабатывались специально для моделирования систем, содержащих взаимодействующие параллельные компоненты, таким образом алгоритмы параллельного программирования и гиперпоточности можно протестировать с помощью сетей Петри.
II. Описание системы
|
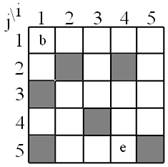
Рис. 1. Лабиринт |
Разрабатываемая система представляет собой лабиринт размерностью 5х5, включающий в себя проходы, стены, клетку входа и клетку выхода. Метка будет начинать движение с клетки “начало” и заканчивать в клетке “конец”.
Лабиринт (рис. 1) задан двухмерным массивом x[i][j]. Элементы массива будет равняться 1 или 0 (0 – проход, 1 – стена).
Реализация системы происходит с помощью UML диаграмм, основанных на алгоритмах из работ [5 - 8].
Вначале, проектируется диаграмма классов (рис. 2), состоящую только из одного класса “робот”, который обращается к массиву лабиринт.
|
Рис. 2. Структурная диаграмма для класса “робот” |
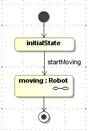
Нужно выделить, что при движение “робота” по лабиринту, в нем будет накапливаться история перемещений. Опираясь на методы разработки программного обеспечения [6 - 8], реализуем структурную диаграмму (рис. 3), состоящую из начального состояния (InitialState) и составного состояния – moving. На рисунке 4 представлено вложенные состояние, описывающее движение “робота”.
Применение комментариев [9] в состояниях, позволяет указать на нюансы, которые должны быть реализованы в сети Петри. В проектируемой системе это сохранение истории передвижений в фишке.
|
Рис. 3. Структурная диаграмма для класса “робот” |
Рис. 4. Состояние moving. |
III. Реализация с помощью сетей Петри
Построение цветной сети Петри (рис. 5) происходит по правилам преобразований UML-сети Петри [6 - 8].
|
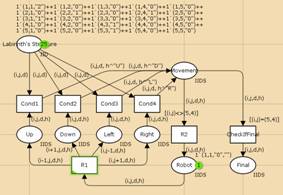
Рис. 5. Цветная сеть Петри, полученная из структурных диаграмм (рис. 3, 4) |
Примечание saveHistory: true, изображенное на рисунке 4, указывает на сохранении истории в метке. Чтобы реализовать сохранение истории была добавлена переменная “h” к местам с типом данных IIDS. При срабатывании одного из переходов Cond1, Cond2, Cond3 and Cond4 к фишке добавляется история перемещений.
Примечания в UML диаграммах могут применяться для построения UML диаграмм, ориентированных на время.
Место Final может содержать только фишки, которые нашли выход из лабиринта. История передвижений, заложенная в фишке, позволяет отследить маршрут, по которому двигался “робот” до клетки “конец”.
IV. Анализ сети Петри
Сеть Петри (рис. 5) была построена в программной среде CPN Tools, которая может быть использована для анализа систем. В ходе анализа системы был сформирован отчёт, представленный в таблице 1.
Таблица 1. Отчет о пространстве состояний для системы (рис. 5).
Statistics |
|
State Space Nodes: 16571 Arcs: 68950 Secs: 300 Status: Partial |
Пространство состояний модели состоит из 16571 узлов, 68950 дуг за 300 секунд . |
Scc Graph Nodes: 16571 Arcs: 68950 Secs: 3 |
|
Home Properties |
|
Home Markings None |
Модель не имеет домашних маркировок. |
Liveness Properties |
|
Dead Markings 6188 [16571,16570,16569, 16568,16567,...] |
Сеть Петри содержит мёртвые маркировки. |
Dead Transition Instances None |
В модели отсутствуют мёртвые переходы. |
Live Transition Instances None |
|
Fairness Properties |
|
No infinite occurrence sequences |
Бесконечные последовательности отсутсвуют. |
В сети присутствуют «мертвые» маркировки, что означает наличие в модели тупиковых состояний. Тупиковые состояния возникают, когда роботы не могут найти выход из лабиринта.
V. Выводы
Представлен механизм преобразования UML диаграмм в сети Петри. Данную методику можно применять для более общего представления UML диаграммам и временных сетей Петри.
Ещё одним важным результатом является сохранение в метке истории её передвижений. История перемещений может дать информацию о движении метки по лабиринту до клетки “конец”, что может быть использовано для анализа систем.
Так как задание массива в программном пакете CPN Tools трудоёмко, можно предложить использование внешних программ, например Excel.
Список литературы
1. Воевода А.А. Марков А.В. О компактном представлении языков сетей Петри: сети с условиями и временные сети: сб. науч. тр. НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2010, № 2. С. 77 – 83.
2. Воевода А.А. Марков А.В. Тестировании UML-диаграмм с помщью аппарата сетей Петри на примере разработки ПО для игры «Змейка: сб. науч. тр. НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2010, №3. С. 51 – 61.
3. Воевода А.А. Романников Д.О. Использование UML и временных сетей Петри при разработке программного обеспечения: сб. науч. тр. НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2010, № 3. С. 61 – 71.
4. Зимаев И.В. О возможности автоматической трансляции UML диаграмм деятельности в сети Петри: сб. науч. тр. НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2010, № 1. С. 149 – 156.
5. Воевода А.А. Романников Д.О. Зимаев И.В. Применение UML-диаграмм и сетей Петри при разработке встраиваемого программного обеспечения: научный вестник НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2009, №4. С. 169 – 175.
6. Коротиков С.В. Применение сетей Петри в разработке программного обеспечения центров дистанционного контроля и управления: дис. канд. техн. Наук / НГТУ. Новосибирск: Изд-во Новосиб. ун-та, 2008.
7. L. Baresi, M. Pezze, On formalizing UML with high-level Petri net, Concurrent object-oriented programming and Petri nets: advances in Petri nets. Berlin: Heidelberg. Springer, 2003. P. 276 – 304.
8. J. Campos, J. Merseguer, On the integration of UML and Petri nets in software development, Lecture Notes in Computer Science. Berlin: Heidelberg. Springer, 2006. P. 19 – 36.
9. S. Bernardi, J. Merseguer Performance evaluation of UML design with Stochastic Well-formed Nets: The Journal of Systems and Software. 2007. -80 р.
дипломов




Оставить комментарий