Статья опубликована в рамках: V Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 14 ноября 2011 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АЛГОРИТМ БЫСТРОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ
Авяшкиева Надежда Сергеевна
аспирант СГУ, г. Ставрополь
преподаватель КГТ-ЭК, г. Элиста
E-mail: nadyusha84@yandex.ru
Настоящий период развития вычислительной техники характеризуется интенсивным поиском новых принципов обработки и хранения информации, построения вычислительных архитектур и систем с привлечением современных технологий, среди которых одной из наиболее востребованных является цифровая обработка сигналов (ЦОС).
Одним из основных направлений ЦОС является спектральный анализ. Мощным инструментом, используемым в методах спектрального анализа, является Фурье-анализ. Для уменьшения количества арифметических операций, требуемых для вычисления дискретного преобразования Фурье (ДПФ),
![]() (1)
(1)
разработан ряд алгоритмов быстрого преобразования Фурье (БПФ). Алгоритмы БПФ характеризуются внутренним параллелизмом, поэтому перспективной является их реализация с помощью системы счисления остаточных классов как системы, обладающей высоким уровнем естественного параллелизма при выполнении арифметических операций.
БПФ по основанию 2 с прореживанием по времени заключается в разбиении исходной последовательности отсчетов ![]() ,
, ![]() на две последовательности длинной
на две последовательности длинной ![]() ,
, ![]() и
и ![]() ,
, ![]() , таких что:
, таких что: ![]() содержит чётные индексы, а
содержит чётные индексы, а ![]() - нечётные,
- нечётные, ![]() [3, с. 123]. С учётом этого формула (1) будет иметь вид (2):
[3, с. 123]. С учётом этого формула (1) будет иметь вид (2):
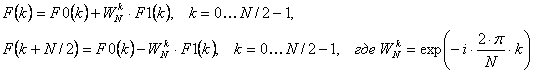 (2)
(2)
Рассмотрим алгоритмы представления и обработки данных в СОК.
Полной системой вычетов по модулю р называется совокупность р-целых чисел, содержащая точно по одному представителю из каждого класса вычетов по модулю р. Каждый класс вычетов по модулю р содержит в точности одно из чисел совокупности всех возможных остатков от деления на р: 0, 1, …, р – 1.
Фундаментальным положением, лежащим в основе модулярного представления чисел, является китайская теорема об остатках (3):
Теорема. Пусть ![]() - попарно взаимно-простые числа, больше 1, и пусть
- попарно взаимно-простые числа, больше 1, и пусть ![]() . Тогда существует единственное неотрицательное решение по модулю Р следующей системы сравнений:
. Тогда существует единственное неотрицательное решение по модулю Р следующей системы сравнений:
![]()
![]() …,
…, ![]() (3)
(3)
Пусть заданы положительные числа ![]() , которые называют основаниями или модулями системы. Обозначим
, которые называют основаниями или модулями системы. Обозначим  . Эта величина характеризует объём диапазона системы [4, с. 9]. Под системой остаточных классов понимают такую непозиционную систему счисления, в которой целое неотрицательное число А можно представить в виде набора остатков от деления этого числа на выбранные основания системы, т. е. (4)
. Эта величина характеризует объём диапазона системы [4, с. 9]. Под системой остаточных классов понимают такую непозиционную систему счисления, в которой целое неотрицательное число А можно представить в виде набора остатков от деления этого числа на выбранные основания системы, т. е. (4)
![]() ,
, 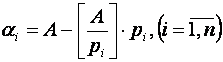 . (4)
. (4)
Можно выделить ряд преимуществ обработки сигналов в СОК:
1) отсутствие межразрядных связей в числе, кодированном вычетами в СОК, позволяет осуществлять независимую обработку сигналов в каналах СОК;
2) малоразрядность остатков приводит к снижению ошибок округления, уменьшению аппаратурных затрат и увеличению быстродействия;
3) ввиду небольшого количества существующих кодовых комбинаций в СОК имеется возможность построения табличной арифметики;
4) реализация принципа конвейерной обработки информации;
5) высокая точность, надежность, алгоритмическая отказоустойчивость и способность к самокоррекции [2, с. 118].
Рассмотрим алгоритм БПФ в СОК, учитывающий свойства целых чисел в коммутативном кольце вычетов, а также схемы его технической реализации.
Метод синтеза устройств БПФ в СОК основан на идее корреляции величины модуля со значением весовых коэффициентов фильтра (или поворачивающих множителей БПФ). Необходимо обеспечить совпадение NS и W (NS и A, B), или сделать их отличными на ±1, ±2. Этапы решения:
1) первоначальный предварительный выбор множества оснований СОК;
2) изменение выбранных оснований с целью их приближения к весовым коэффициентам (до W=NS±1 или ![]() ) путем введения нормирующего множителя M;
) путем введения нормирующего множителя M;
3) подсчет аппаратурных затрат и быстродействия во всех случаях;
4) вычисление погрешностей.
Наибольшее влияние на число каналов БПФ в СОК оказывают максимальный диапазон результата rmax, который зависит от числа отсчетов N, разрядности R данных x(n) и разрядности RW весовых коэффициентов Wk:
![]() , где N1=N/2.
, где N1=N/2.
Величина RW выбирается, исходя либо из точности дискретизации e1, либо из заданного отношения среднеквадратичного значения (СКЗ) ошибки к СКЗ сигнала e2, либо принимается, что RW=R.
Для теоретического определения числа каналов и модулей СОК при реализации N-точечного БПФ в качестве основного использовалось соотношение:
![]() .
.
Результаты программного синтеза показали, что практически максимально возможный результат не превышает 218 для большинства алгоритмов.
Для осуществления вычислительной операции «бабочка» в каждом S-м канале СОК необходимо провести операции сложения и умножения по соответствующему модулю (будем рассматривать случай прореживания по времени):
![]() ;
; ![]() ;
;
где ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Для уменьшения аппаратурных затрат и увеличения быстродействия предложено, во-первых, построение табличных модулей (ТМ), реализующих операцию «бабочка» в СОК с использованием соотношений:![]() ;
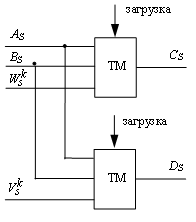
; ![]() . Вариант одной из схем базовых ТМ, реализующих операцию «бабочка» в СОК для RS=3...4, представлен на рис.1. В качестве таблиц возможно использование ППЗУ (в неперестраиваемых структурах) и сверхоперативных ЗУ, загружаемых из основной памяти таблицами выполняемых арифметических операций. Операнды подаются на шину адреса ТМ, с информационных выходов которых снимаются числа CS и DS. При RSmax£3...4 объем памяти ТМ составляет 256 байт, а при RSmax=5...6 – не превышает 4 Кб, что не составляет проблем при технической реализации. Во-вторых, предлагается реализация функциональных модулей СОК на комбинационных операционных схемах (КОС), выполненных в виде заказных СБИС или синтезированных на ПЛМ (ПЛИС). На рис. 2 показана схема, в которой совмещен ряд логических операций «И» и «ИЛИ». В-третьих, предложено использовать логический подход к построению блока формирования весовых коэффициентов для его упрощения (уменьшается объём таблиц ППЗУ в вычислительном блоке определения CS и DS): если
. Вариант одной из схем базовых ТМ, реализующих операцию «бабочка» в СОК для RS=3...4, представлен на рис.1. В качестве таблиц возможно использование ППЗУ (в неперестраиваемых структурах) и сверхоперативных ЗУ, загружаемых из основной памяти таблицами выполняемых арифметических операций. Операнды подаются на шину адреса ТМ, с информационных выходов которых снимаются числа CS и DS. При RSmax£3...4 объем памяти ТМ составляет 256 байт, а при RSmax=5...6 – не превышает 4 Кб, что не составляет проблем при технической реализации. Во-вторых, предлагается реализация функциональных модулей СОК на комбинационных операционных схемах (КОС), выполненных в виде заказных СБИС или синтезированных на ПЛМ (ПЛИС). На рис. 2 показана схема, в которой совмещен ряд логических операций «И» и «ИЛИ». В-третьих, предложено использовать логический подход к построению блока формирования весовых коэффициентов для его упрощения (уменьшается объём таблиц ППЗУ в вычислительном блоке определения CS и DS): если ![]() , то
, то ![]() . Эти соотношения реализуются в виде комбинационных схем, представленных на рис. 3. [1, с. 21].
. Эти соотношения реализуются в виде комбинационных схем, представленных на рис. 3. [1, с. 21].
Рисунок 1. Схема базового ТМ для RS=3...4 |
Рисунок 2. Схема СБИС на КОС для вычисления БПФ в СОК |
|
|
Рисунок 3. Комбинационная схема для NS=5, 7

Список литературы:
1. Галанина Н. А. Методы и вычислительные устройства цифровой обработки сигналов в системе остаточных классов. Автореф. дис. докт. техн. наук. – Казань, 2010. – 35 с.
2. Лебедев Е. К. Оптимальные алгоритмы БПФ в СОК // Перспективные технологии в средствах передачи информации: сб. тезисов докл. Междунар. конф.– Владимир: Изд-во Влад. политех. ун-та, 1995.– с. 118–119.
3. Цифровая обработка сигналов: Учебн. Пособие для вузов/Л. М. Гольденберг, Б. Д. Матюшкин, М. Н. Поляк. – 2изд., перераб. и доп. – М.: Радио и связь, 1990. – 256 с.: ил.
4. Червяков Н. И. и др. Нейрокомпьютеры в системе остаточных классов. Кн. 11: Учебное пособие для вузов.- М.: Радиотехника, 2003, - с. 272.
дипломов



Оставить комментарий