Статья опубликована в рамках: V Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 14 ноября 2011 г.)
Наука: Технические науки
Секция: Приборостроение, метрология, радиотехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МНОГОМЕРНЫЕ ФУНКЦИЙ РАССЕЯНИЯ КАНАЛА РАСПРОСТРАНЕНИЯ РАДИОВОЛН НАД СЛУЧАЙНО-ШЕРОХОВАТОЙ ПОДСТИЛАЮЩЕЙ ПОВЕРХНОСТЬЮ
Захаров Фёдор Николаевич
аспирант, ТУСУР, г. Томск,
Поверхности реальных тел всегда в той или иной степени неровны, в силу чего отражение и преломление волн на этих поверхностях сопровождаются явлениями, которые отсутствуют в случае идеально гладких границ раздела. Степень «гладкости» определяется в первую очередь соотношением между длиной волны и геометрическими параметрами неровностей.
Характер рассеяния определяется многими факторами. Кроме размеров неровностей и длины волны падающего излучения, играют роль размеры рассеивающей площади, способ её облучения, а также поляризация первичной волны, отражающие и преломляющие свойства вещества и т. д. В зависимости от соотношения между различными параметрами применяют те или иные приближённые методы расчёта рассеянного поля [4]. Два наиболее простых и часто применяемых метода – это метод малых возмущений и метод Кирхгофа. Метод малых возмущений пригоден для описания поверхностей с малыми неровностями, причём наклоны поверхности должны быть меньше единицы. Приближение Кирхгофа применимо для поверхности с радиусами кривизны, значительно превышающими длину волны [3].
В литературе достаточно подробно описано рассеяние волн на объёмных неоднородностях и на неровной поверхности и получено много данных о корреляционных характеристиках поля при единственном источнике излучения электромагнитных волн и разнесении точек наблюдения. Работ, в которых рассматривается совместное разнесение источников и приёмников, очень мало. В частности, в статье [5] рассматривается отражение волн от случайно-неровной поверхности при малых углах падения для случая горизонтального разнесения точек излучения и точек наблюдения, а в работе [1] — для случая произвольных разнесений точек излучения и точек наблюдения, но при рассеянии волн на объёмных неоднородностях. В связи с этим целью данной работы является создание математической модели многомерной функции когерентности рассеянного поля для случая совместного пространственного разнесения источников и приемников по горизонтали поперёк трассы распространения радиоволн (РРВ). Функция когерентности и функция рассеяния связаны между собой парой преобразований Фурье.
При выводе функции будем рассматривать только случай, характерный для приземных трасс, когда источники и приёмники располагаются на небольшой высоте над поверхностью земли, т.е. волна распространяется под малыми углами к подстилающей поверхности.
Расположим оси декартовой системы координат (x, y, z) так, чтобы ось Ox была направлена вдоль трассы по поверхности земли, а ось Oz – вертикально. Пусть высота в среднем плоской земной поверхности описывается статистически однородной изотропной нормальной случайной функцией h(x,y), среднее значение и дисперсия которой равны нулю и σh2 соответственно, а ковариационная функция имеет гауссовскую форму
|
|
(1) |
где ![]() ,
,
l(x) – среднеквадратическая ширина ковариационной функции (радиус корреляции).
Поскольку область, существенная для РРВ микроволнового диапазона, обычно бывает достаточно узкой в направлении поперек трассы, мы не учитываем зависимости ![]() и
и ![]() от четвертой переменной
от четвертой переменной ![]() .
.
Два ненаправленных источника расположены на одной высоте и разнесены поперек трассы, то есть имеют декартовы координаты (xи , yи1, Dи) и (xи , yи2, Dи), а такие же две точки наблюдения характеризуются координатами (xп, yп1, Dп) и (xп, yп2, Dп). Будем рассматривать две независимые пары источников и приёмников: Источник 1 – Приёмник 1, Источник 2 – Приёмник 2.
В микроволновом диапазоне горизонтальные размеры неоднородностей земной поверхности существенно больше длины волны, поэтому для решения данной задачи воспользуемся методом Кирхгофа: с точностью до постоянной напряжённость электромагнитного поля в точке наблюдения определяется суммой волн, отражённых от каждой точки земной поверхности [4]
|
|
(2) |
где Dи – высота расположения источников;
Dп – высота расположения приёмников;
k = 2π / λ – волновое число,
γ(x) и θ(x) – угол падения луча из источника в точку (x, y) на поверхности земли и такой же угол «отражения» луча, попадающего в точку наблюдения.
Хорошо видно, что затенения отдельных участков отражающей поверхности в этой формуле не учитываются, в противном случае методика анализа существенно усложняется из-за необходимости учитывать дифракционные эффекты и многократное рассеяние. Это предположение с большой вероятностью можно считать справедливым, если выполняется условие
|
|
(3) |
где r = xп – xи – длина трассы РРВ;
S = σh / l – параметр, характеризующий типичное значение углов наклона неровностей отражающей поверхности.
В (2) множитель перед экспонентой учитывает дистанционное ослабление сигнала на трассе РРВ. Слагаемые в показателе экспоненты определяют длину пути распространения сигнала при его отражении от точки неровной поверхности с координатами (x, y).
Математическое ожидание выражения (2) определяет комплексную амплитуду зеркально отражённого луча в каждой из точек наблюдения. Полагая, что высоты расположения источников (Dи) и приёмников (Dп) и область интегрирования поперёк трассы (y) малы по сравнению с длиной трассы РРВ, разлагаем раздельно в ряды по степеням малых параметров выражения, стоящие в показателе экспоненты и перед ней в (2), сохраняя минимально необходимое число членов разложения. Далее воспользуемся [4] известным соотношением M[exp(iz)] = exp[–M(z2)/2], где М – оператор вычисления математического ожидания. И, наконец, интегрируем по переменной y, при этом используем табличный интеграл [2] для экспоненты с квадратичным показателем. В итоге получаем
|
|
(4) |
где 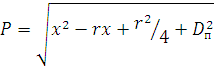 ;
; 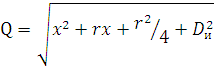
Функцию когерентности определим как математическое ожидание от произведения напряжённостей поля в наблюдаемых точках:
|
|
(5) |
где звёздочка – знак комплексного сопряжения.
В результате расчётов с учётом тех же допущений и предположения, что величины разнесения источников Δyи = yи2 – yи1 и приёмников Δyп = yп2 – yп1 малы по сравнению с длиной трассы, получаем следующее выражение для функции когерентности
|
|
(6) |
На рисунке 1 для примера представлено семейство равных уровней функции когерентности в координатах (Δyи, Δyп), а её сечение при фиксированном значении разнесения источников – на рисунке 2. Графики получены при следующих значениях параметров: λ = 3 см, Dи = Dп = 7 м, r = 1 км, σh = 0,03 м, l = 1 м.
Рисунок 1. Эллипс равных сечений функции когерентности

Абсолютный максимум функции достигается при нулевых значениях разнесений источников и приёмников. Локальный максимум при фиксированном значении одного из разнесений достигается при равном по модулю и противоположном по знаку значении второго разнесения.
Рисунок 2. Сечение функции когерентности плоскостью Δyи = 5 м для трёх значений высот источников и приёмников:
1 – Dи = Dп = 7 м; 2 – Dи = Dп = 10 м; 3 – Dи = Dп = 15 м.

При анализе эллипса равных сечений (рисунок 1) удобно использовать коэффициент эллиптичности сечения равных уровней когерентности
|
|
(7) |
где а и b – значения главных осей эллипса.
Из определения следует, что ![]() . В [1] показано, что при РРВ в случайно-неоднородной среде оба предельных значения параметра
. В [1] показано, что при РРВ в случайно-неоднородной среде оба предельных значения параметра ![]() (0 и 1) соответствуют двум вырожденным случаям:
(0 и 1) соответствуют двум вырожденным случаям: ![]() означает, что все случайные неоднородности среды сосредоточены в бесконечно тонком плоском случайном экране, размещенном посреди трассы; при
означает, что все случайные неоднородности среды сосредоточены в бесконечно тонком плоском случайном экране, размещенном посреди трассы; при ![]() предполагается, что все неоднородности сконцентрированы в двух одинаковых (в среднем) плоских случайных экранах, прилегающих к апертурам передающих и приемных антенн. Если же неоднородности равномерно распределены вдоль трассы, то
предполагается, что все неоднородности сконцентрированы в двух одинаковых (в среднем) плоских случайных экранах, прилегающих к апертурам передающих и приемных антенн. Если же неоднородности равномерно распределены вдоль трассы, то ![]() . Анализ выражения (6) показывает, что подобные свойства параметра
. Анализ выражения (6) показывает, что подобные свойства параметра ![]() характеризовать относительный продольный размер области, существенной для рассеяния волн, присутствуют и в случае рассеяния волн на неровной поверхности, свойства которой меняются вдоль трассы.
характеризовать относительный продольный размер области, существенной для рассеяния волн, присутствуют и в случае рассеяния волн на неровной поверхности, свойства которой меняются вдоль трассы.
Проведённый анализ показал, что коэффициент эллиптичности ξ имеет степенную зависимость от параметра S. Это позволяет по измеренной корреляции отражённых сигналов определить статистические параметры неровностей отражающей поверхности.
На рисунке 3 представлена зависимость формы функции когерентности от параметра S, который характеризует соотношение поперечных и продольных размеров неровностей отражающей поверхности.
Рисунок 3. Зависимости формы функции когерентности на расходящихся трассах от параметра неровной поверхности S
1 – S = 0,01; 2 – S = 0,02; 3 – S = 0,04.

Из рисунка 3 видно, что с увеличением S ширина функции уменьшается и стремиться к постоянному значению. Маленькой величине S соответствуют либо маленькие высоты неровностей, либо большие горизонтальные размеры элементов рельефа отражающей поверхности. В этом случае поверхность становится ровной с плавным изменением уровня, т.е. отражение практически зеркальное.
Статистические характеристики подстилающей поверхности (СКО высоты неровностей и интервал пространственной корреляции) определяются по электронным картам местности при стандартной обработке двумерного профиля.
Полученные результаты позволяют численно определить следующие параметры для заданных значений высот источников и приёмников и их разнесений с учётом знака:
1) плотность потока мощности в свободном пространстве для ненаправленного источника единичной мощности
|
|
(8) |
где ![]() – длина пути распространения луча;
– длина пути распространения луча;
2) ожидаемую комплексную амплитуду напряжённости поля
|
|
(9) |
3) комплексную амплитуду зеркально отражённого луча, численно вычислив значение интеграла (4). Шаг интегрирования по x должен равняться (0,2 … 0,3)∙l, но не более 0,01r.
4) суммарную амплитуду регулярного сигнала
|
|
(10) |
5) множитель ослабления для рассеянной составляющей поля в точках приёма
|
|
(11) |
6) по формуле (6) значение коэффициента корреляции сигналов в точках приёма.
Чтобы построить пространственную функцию когерентности, необходимо провести расчёты по пункту 6) для различных значений разнесений источников и приёмников.
Проведённый анализ показал, что функция когерентности достигает максимума при противоположных по знаку и равных по модулю значениях разнесениях источников и приёмников. Если использовать терминологию, применяемую в [1], то это так называемые «пересекающиеся» трассы, корреляция сигналов на которых максимальна. На «параллельных» трассах (разносы равны по модулю и по знаку) корреляция низкая и зависит от абсолютных значений разносов. Промежуточным является случай «расходящихся» или «сходящихся» трасс, когда один из разносов намного больше другого.
Зависимость функции когерентности от параметров неровной отражающей поверхности в общем случае определяется параметром S, который характеризует вертикальные и горизонтальные размеры неоднородностей. С увеличением этого параметра интервал корреляции уменьшается.
Полученные модели могут использоваться для оценки статистических характеристик полей и радиосигналов на выходах антенн в радиотехнических системах различного назначения, работающих на приземных трассах. В частности, в системах диагностики и прогнозирования условий распространения УКВ в тропосфере.
Список литературы:
1. Акулиничев Ю.П., Голиков А.М. Анализ корреляционных характеристик случайно-неоднородных каналов при комплексном разнесении источников и приемников // Радиотехника и электроника. – 1987. – Т.32, вып.8. – С. 1646 – 1654.
2. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Государственное издательство физико-математической литературы, 1963. – 1108 с.
3. Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. Том 2. М.: Мир, 1981. – 280 с., ил.
4. Рытов С.М., Кравцов Ю.А. Татарский В.И. Введение в статистическую радиофизику. Часть 2. Случайные поля. М.: Наука, 1978. – 464 с., ил.
5. Chan T. K., Y. Kuga, A. Ishimaru. Angular memory effect of millimeter-wave scattering from two-dimensional conducting random rough surfaces // Radio Science.– 1995, V. 31.– P. 1067 – 1076.
дипломов


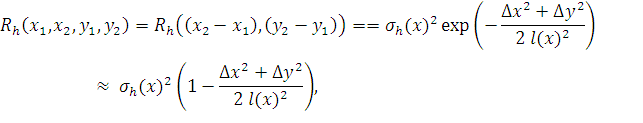
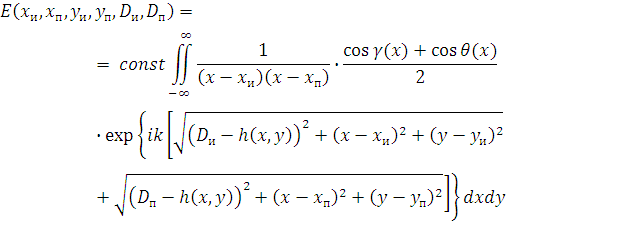
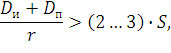

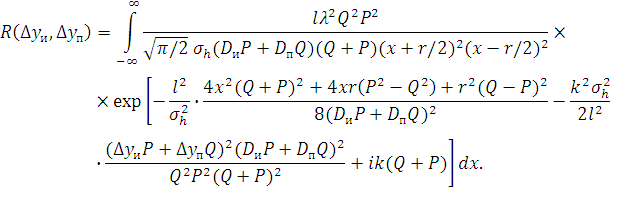
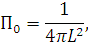
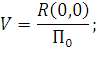
Оставить комментарий