Статья опубликована в рамках: V Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 14 ноября 2011 г.)
Наука: Технические науки
Секция: Аэрокосмическая техника и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АНАЛИЗ ПРОЧНОСТИ ТОРСИОНА НЕСУЩЕГО ВИНТА ВЕРТОЛЕТА МЕТОДОМ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Горелов Алексей Вячеславович
соискатель, КНИТУ им. А. Н. Туполева, г. Казань
Е-mail: a.gorelov@inbox.ru
В настоящее время наряду с классическими трехшарнирными втулками несущего винта (НВ) все более широкое распространение получают бесшарнирные втулки с упругими элементами торсионного типа. Исследованный в работе торсион представляет склеенную слоистую стеклопластиковую балку, которая применяется во втулке НВ вертолета «Ансат».
В работе проведены расчеты по определению параметров напряженно-деформированного состояния (НДС) элементов торсиона НВ при полетных нагружениях. Выявлены наиболее нагруженные места в резиновых слоях и для снижения напряжений предложена измененная укладка резиновых слоев в комлевой и концевой частях в виде клиновидного изменения длины слоев по толщине.
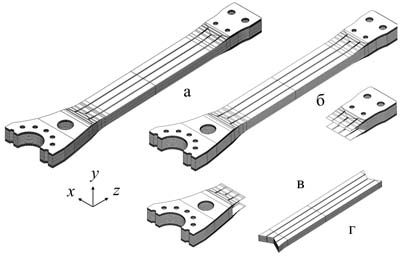
На рис. 1 а показана геометрическая модель исходного рукава торсиона, построенная на основе чертежей предоставленных разработчиками. Торсион состоит из слоев стеклоткани Т-25(ВМ) с углами армирования по отношению к продольной оси – 0º (рис. 1 б), ±45º (рис. 1 в) а также (рис. 1 г). Слои резины являются продолжением слоев стеклоткани Т-25 с углами армирования ±45º. Все соединения выполнены склеиванием.
C помощью пакета программ SolidWorks построена геометрическая модель рукава торсиона. Слои материала, имеющие одинаковые физико-механические характеристики, моделировались в SolidWorks с помощью операции «Разделить» и представлялись отдельными телами (рис. 1 б, в, г).
На основе геометрической модели SolidWorks с помощью конечно-элементного (КЭ) пакета программ ANSYS на языке APDL создана КЭ модель рукава торсиона. Для этого модель частями (рис. 1 б, в, г) из SolidWorks сохранялась в файл формата x_t (Parasolid), а затем импортировалась программой ANSYS.
Рисунок 1. Геометрическая модель рукава торсиона: а – в сборе; б – слои стеклоткани Т-25 (0º); в – слои стеклоткани Т-25 (±45º); г – слои резины Р-181
При расчете НДС рукава торсиона для материалов его элементов использовалась модель упругого деформирования ортотропного материала. Пара слоев с углами армирования ±45º заменялась материалом из одного слоя. Такой подход описан в работе [1].
В табл. 1 представлены физико-механические характеристики (ФМХ) материалов, которые использовались при расчетах.
Таблица 1. Физико-механические характеристики материалов
Материал |
Модули упругости при растяжении и сдвиге, МПа |
Коэффициенты Пуассона |
|||||||
|
|
|
|
|
|
|
|
|
|
Т25 (0º) |
18300 |
3300 |
49000 |
1300 |
1300 |
6170 |
0,35 |
0,015 |
0,084031 |
Т25 (±45º) |
18689 |
3300 |
18689 |
1300 |
1300 |
15051 |
0,16582 |
0,02928 |
0,51451 |
Р-181 |
6 |
2,013 |
0,49 |
||||||
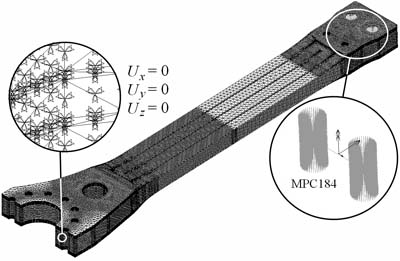
При разбиении торсиона на КЭ, в виду сложности конструкции использовались 10-ти узловые трехмерные квадратичные КЭ SOLID187 в форме четырехгранника [2] (рис. 2). Для моделирования действия болтов крепления лопасти к торсиону в концевой части и приложения внешних нагрузок со стороны лопасти использовался элемент многоточечных связей MPC184 с включенной опцией жесткой балки [2] (рис. 2).
Рисунок 2. Конечно-элементная модель рукава торсиона и граничные условия
Конечно-элементную модель рукава торсиона, для задания свойств материалам, условно, можно разделить на две части – комлевую жесткую (выделена рамкой на рис. 3) и жестко-упругую с концевой (рис 3). Комлевой жесткой части свойства материала назначались в глобальных осях x, y, z (рис. 1), а жестко-упругой с концевой в специально введенной локальной системе координат повернутой на угол конусности –2,5º вокруг оси x.
Рисунок 3. Конечно-элементная модель рукава торсиона (вид сбоку)

КЭ модель рукава торсиона (рис. 2) насчитывает около 1,27 млн. элементов (и приблизительно 5,3 млн. степеней свободы) из них приходится на элементы с материалом: Т-25 (0º) – 0,65 млн.; Т-25 (±45º) – 0,55 млн.; Р-181 – 0,06 млн. На элементы жестких связей – 0,01 млн.
Кинематические и статические граничные условия, накладываемые на КЭ модель торсиона воспроизводят поведение реальной конструкции. А именно, имитируют: неподвижное болтовое соединение комлевой части торсиона с втулкой несущего винта (заданы нулевые векторы перемещений узлов ![]() на поверхностях отверстий комлевой части (рис. 2)); действие лопасти на торсион в виде статически эквивалентных сосредоточенных сил и моментов.
на поверхностях отверстий комлевой части (рис. 2)); действие лопасти на торсион в виде статически эквивалентных сосредоточенных сил и моментов.
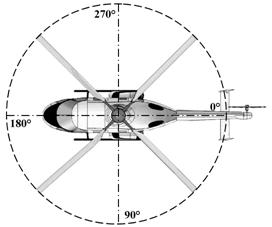
Сосредоточенные силы и моменты, статически эквивалентные силовому действию лопасти на торсион, прикладывались к узлу, расположенному на оси торсиона и передавались на торсион с помощью жестких балочных КЭ связи (стрелки на рис. 2). В табл. 2 приведены нагрузки соответствующие азимутальным углам ![]() 150º и 330º (рис. 4) при скорости полета 220 км/ч.
150º и 330º (рис. 4) при скорости полета 220 км/ч.
Таблица 2. Нагрузки в зависимости от азимутального угла ![]()
|
|
|
|
|
|
150 |
-3390,5 |
3500 |
3885,1 |
1357,3 |
161820,2 |
330 |
2859,6 |
1100 |
-4861,3 |
-2906,5 |
161892 |
Рисунок 4. Схема вращательного движения несущего винта
При решении алгебраической системы уравнений, получаемой с помощью вариационного принципа и КЭ модели рукава торсиона, использовался метод сопряженных градиентов (PCG-решатель в ANSYS). Время счета одного варианта расчета составило около 1 ч.
В результате расчета параметров НДС исходного конструктивного исполнения рукава торсиона при полетной нагрузке (табл. 2) построены линии уровней полей напряжений, и перемещений с усреднением результатов по узлам (в работе не приводятся из-за ограничения по объему статьи). Расчеты показали что при нагрузках, указанных в табл. 2, происходит изменение знака компонент перемещений, а также нормальных и касательных напряжений в комлевой и концевой частях торсиона за один оборот лопасти. Экстремальных значений в слоях резины напряжения достигали в комлевой и (или) концевой частях рукава торсиона.
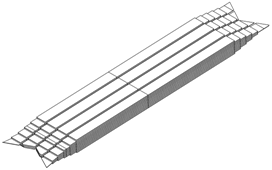
С целью уменьшения напряжений влияющих на расслоение в резиновых слоях (рис. 1 г) предложен модифицированный вариант исполнения рукава торсиона. Модификация заключается в клиновидном изменении длины резиновых слоев в комлевой и концевой частях торсиона по их толщине (рис. 5). При этом укороченные резиновые слои аналогично исходной конструкции также продолжаются слоями стеклопластика Т-25 (±45º).
Рисунок 5. Слои резины Р-181 в модифицированном варианте рукава торсиона
В табл. 3 приведены максимальные и минимальные значения перемещений ![]() ,
, ![]() результатов расчетов, а также представлены повороты
результатов расчетов, а также представлены повороты ![]() концевой части исходного и модифицированного торсионов при крутящем моменте в концевой части
концевой части исходного и модифицированного торсионов при крутящем моменте в концевой части ![]() = 100 Н·м.
= 100 Н·м.
Таблица 3. Значения перемещений результатов расчетов
|
Вариант геометрии ( |
|||
Исходный (150) |
Модифицированный (150) |
Исходный (330) |
Модифицированный (330) |
|
|
17,3 |
16,9 |
-12,1 |
-11,9 |
|
81,4 |
77,6 |
-103,8 |
-97,6 |
|
Исходный |
Модифицированный |
||
0,341 |
0,308 |
|||
На основании результатов расчетов построены гистограммы минимальных и максимальных напряжений для исходного и модифицированного вариантов конструктивного исполнения рукава торсиона (рис. 6 – 8). Напряжения на рис. 6 – 8 указаны в МПа.
На основе результатов расчета, представленных в виде табл. 3 и гистограмм на рис. 6 – 8, можно сделать предварительные выводы по эффективности предложенных конструктивных изменений.
Рисунок 6. Гистограмма в слоях стеклопластика Т-25 (0º): а – минимальных напряжений; б – максимальных напряжений
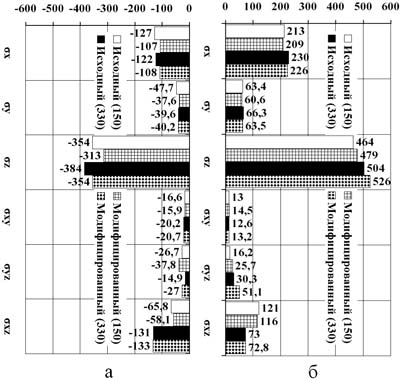
Рисунок 7. Гистограмма в слоях стеклопластика Т-25 (±45º): а – минимальных напряжений; б – максимальных напряжений
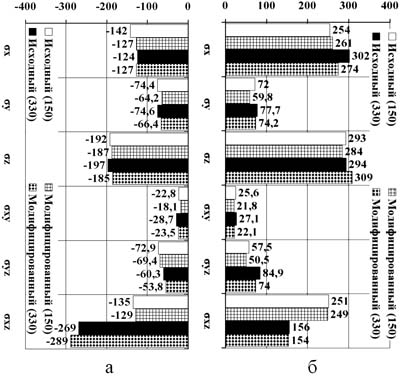
Рисунок 8. Гистограмма в слоях резины Р-181: а – минимальных напряжений; б – максимальных напряжений

В модифицированном торсионе наблюдается: снижение максимальных положительных нормальных напряжений в резиновых слоях на величину ~ 39% и более на фоне незначительного увеличения касательных напряжений в этих слоях; снижение податливости концевой части торсиона при изгибе в плоскости вращения на величину ~ 2%, при изгибе в плоскости взмаха на величину ~ 6%, при кручении относительно оси торсиона на величину ~ 9,7%.
Список литературы:
1. Савинов В. И. Расчет напряженно-деформированного состояния композиционных стержневых конструкций несущей системы вертолета. Автореферат диссертации на соискание ученой степени кандидата технических наук. Казань: КГТУ, 1999. - 16 с.
2. Басов К.А. ANSYS: справочник пользователя. М.: ДМК Пресс, 2005.-640 с.
дипломов






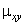

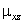
Оставить комментарий