АНАЛИЗ РИСКА ТЕХНОЛОГИЧЕСКИХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ МЕТОДА МОНТЕ-КАРЛО

RISK ANALYSIS OF TECHNOLOGICAL SYSTEMS USING THE METHOD OF MONTE-CARLO

Anatoliy Kozlitin

doctor of technical Sciences, professor

Saratov State Technical University of Yuri Gagarin, Russia, Saratov

Pavel Kozlitin

candidate of technical Sciences, associate professor, the leading expert

of 604th military representation of the Ministry of defence

of the Russian Federation, Russia, Saratov

АННОТАЦИЯ

В статье рассматриваются подходы и методы, которые позволяют получить модель потенциального риска технологической системы в условиях объективной ограниченности исходной информации. В основу метода анализа риска технологической системы, которая является источником аварийных выбросов, положен метод Монте-Карло.

ABSTRACT

Article describes approaches and methods which allow to receive model of potential risk of technological system in the conditions of objectively limited initial information. The base of a method of the analysis of risk of technological system which is a source of emergency emissions, is the method of Monte-Carlo.

Ключевые слова: риск, авария, аварийная ситуация, безопасность, технологический блок, сценарии аварийной ситуации, потенциальный риск, метод Монте-Карло.

Keywords: risk, accident, accident situation, safety, technological block, accident situation scenarios, potential risk, method Monte-Carlo.

В конце 70-х, начале 80-х годов прошлого столетия отмечается небывалый рост промышленного производства. Энергонасыщенность промышленных объектов становится колоссальной. В техносфере сосредотачиваются большие потенциальные опасности, связанные с возможностью возникновения промышленных аварий и  чрезвы­чайных ситуаций антропогенного характера.

Как следствие техногенные аварии и катастрофы становятся объективной реальностью техносферы, вероятность возникновения которых никогда не равна нулю, как и вероятность экстремальных природных явлений.

В этих условиях превалирующей посылкой современной концепции безопасности в техносфере становится признание опасности как внутреннего свойства «объекта». То есть опасность – это ситуация, которая всегда присутствует на «объекте» и может, с определенной вероятностью, причинить вред человеку и окружающей среде, за счет запасенной внутри «объекта» энергии или химически и биологически опасных веществ, и материалов. Следовательно, можно утверждать – нулевой риск не возможен в сложных технических системах.

Как следствие определяющей становится концепция «прием­лемого риска», в основе которой заложен принцип «предвидеть и предупредить». Эта концепция предусматривает возможность аварии и соответственно меры по предотвращению ее возникновения и развития.

Естественно возникает вопрос – до какого уровня мы можем снижать вероятность аварии Р(А), т. е. какой уровень безопасности является приемлемым? Для ответа на данный вопрос необходимо иметь соответствующую меру для количественного измерения опасности. В качестве такой меры введено понятие техногенного риска.

Риск R(Y) – это мера опасности, характеризующая вероятность возникновения и развития аварии на опасном производственном объекте и тяжесть ее последствий

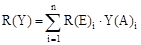.                                                                              (1)

Тяжесть последствий от воздействия поражающего фактора аварии (взрыв, пожар или токсическое воздействие) характеризуется уровнем ущерб Y(A), наносимого человеку и инфраструктуре объекта. Вероятность возникновения и развития аварии описывается потенциальным риском R(E) – стохастической (вероятностной) составляющей ожидаемого ущерба.

Наиболее полно и, с нашей точки зрения [1], адекватно существу проблемы анализа потенциальной опасности промышленного объекта соответствует потенциальный риск, представленный интегральной формулой полной вероятности:

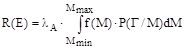,                                                                             (2)

где:   f(M) – плотность распределения вероятностей реализации аварийных выбросов на объекте;

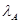– вероятность аварии на опасном производственном объекте c формированием рассматриваемого поражающего фактора;

P(Г/М) – вероятность поражения реципиента в рассматриваемой точке пространства при условии аварийного выброса опасного вещества (определяется координатным законом поражения реципиента);

Г – расстояние от места аварии до рассматриваемой точки пространства;

М – масса аварийного выброса опасного вещества;

[М_min, М_max] – диапазон изменения массы аварийных выбросов на потенциально опасном объекте.

Основным показателем тяжести последствий аварийного выброса на исследуемом потенциально опасном объекте является величина массы вещества (М), участвующего в создании поражающего фактора. Величина массы аварийного выброса является случайной величиной и  характеризуется соответствующим вероятностным распределением f(M).

В этой связи возникает необходимость, основываясь на клас­сических методах теории вероятностей, разработать подходы и методы, позволяющие в условиях объективно ограниченной исходной информации получить модель и параметры плотности распределения случайной величины M – массы неконтролируемых выбросов опасного вещества.

В основу метода анализа сложной технической системы как источ­ника аварийных выбросов, позволяющего определить функцию f(M) нами положен метод статистических испытаний Монте-Карло [2]. Данный метод позволяет генерировать значительную по объему (более миллиона) выборку случайных величин, определяющих распределение масс аварийных выбросов на объекте.

Рассмотрим алгоритм моделирования функции f(M) на основе метода Монте-Карло, который включает следующие основные этапы:

·           выбор математической модели и варьируемых параметров аварийного истечения опасного вещества из аварийного блока;

·           определение стандартных распределений вероятностей варьируемых параметров выбранной математической модели;

·           генерирование псевдослучайных выборок варьируемых параметров из этих стандартных распределений и получение псевдослучайной выборки массы аварийных выбросов опасного вещества;

·           статистическая обработка полученного массива данных и  определение модели и параметров плотности распределения массы аварийных выбросов.

В качестве модели истечения жидкости из рассматриваемого аварийного оборудования рассмотрим формулу, описывающую зависимость массового расхода жидкой фазы q_вбр от физических условий содержания опасного вещества в аварийном блоке и параметров аварийного истечения (на примере разгерметизации резервуара, рис. 1).

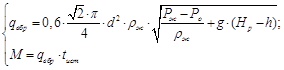                                                                                                                                (3)

Из выражения (3) можно видеть, что масса аварийного выброса является функцией следующих случайных параметров: диаметра аварийного отверстия d, высоты расположения аварийного отверстия h, высоты жидкости в резервуаре Н_Р, давления в аварийном блоке Р_ж, времени истечения опасной жидкости t_ист.

Принимая для рассматриваемых сценариев развития аварии в  качестве основных случайные параметры d_i и h_i, массу аварийного выброса будем определять по функциональной зависимости М_i=f(d_i,h_i) при Р_ж= const и t_истi = const.

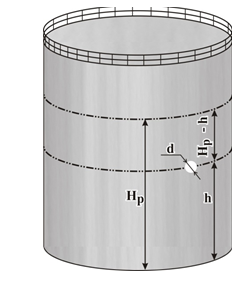
Рисунок 1. Разгерметизация резервуара

На следующем этапе определения функции f(M), исходя из данных о ретроспективной информации по отказам оборудования на  конкретном химически опасном объекте, в качестве стандартных распределений вероятностей нами использовались для условного диаметра аварийного отверстия d – нормальное распределение, для  высоты аварийного отверстия h – показательное распределение, рис. 2.

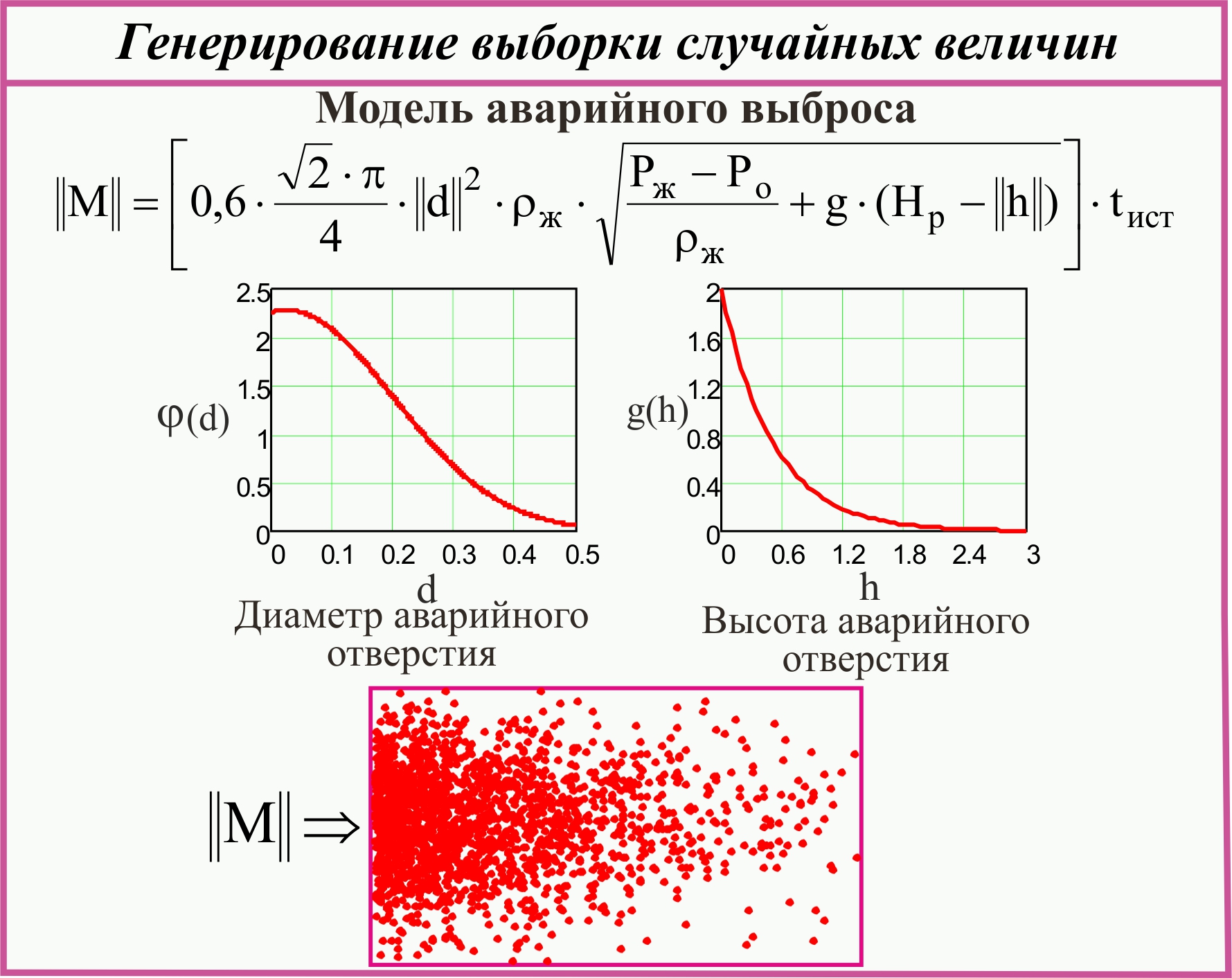
Рисунок 2. Алгоритм генерирования выборки случайных чисел

Генерирование псевдослучайных выборок варьируемых параметров d и h из этих стандартных распределений выполнялось в программе Mathcad, используя соответствующие встроенные функции генератора случайных чисел соответственно d = rnorm(n,m,s) и  h  =  rexp(n,λ), где n – задаваемое число случайных чисел (n > 500), m  – математическое ожидание и s – среднеквадратическое отклонение рассматриваемого нормального распределения, λ – параметр экспонен­циального распределения.

По результатам расчетов определяются соответствующие вектора d и h, рис. 3.

Рисунок 3. Сгенерированные псевдослучайные выборки

параметров d и h

На основе полученных случайных выборок диаметра аварийного отверстия d и высоты расположения отверстия h при фиксируемом значении остальных величин в выражении (3) определяется множество неконтролируемых выбросов опасного вещества и формируется матрица масс 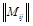. Вид матрицы полученной псевдослучайной выборки масс показан на рис. 4.

Рисунок 4. Псевдослучайная выборка массы аварийных выбросов

Выполнив статистическую обработку полученного массива данных 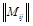, определяется модель и параметры плотности распределения массы аварийных выбросов f(M). По виду гистограммы статистической плотности распределения в первом приближении визуально оценивается возможная функция распределения случайной величины, рис. 5.

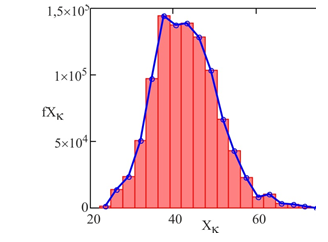
Рисунок 5. График статистической плотности распределения массы выбросов

После получения эмпирического распределения производится подбор теоретического закона распределения, пригодного для описания вероятностных свойств изучаемой случайной величины. В соответствии с центральной предельной теоремой при росте размера выборки распределение будет стремиться к нормальному распределению. В качестве достаточно «большого» объема выборки принимается N не менее 100. По результатам статистических испытаний Монте-Карло объем смоделированной выборки составил N = 4  10⁶ случайных аварийных выбросов.

На основе полученной случайной выборки оцениваются параметры модели (гипотетической функции распределения): m  –  среднее значение массы аварийных выбросов, s – среднеквадра­тическое отклонение и определяется модель плотности распределения массы аварийных выбросов f(M), рис. 6.

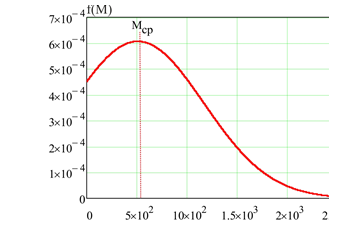
Рисунок 6. График плотности распределения массы выбросов

Функция f(M) – важная характеристика технической системы, определяющая опасность объекта, как источника аварийных выбросов, кривой плотности распределения относительных частот, построенной для различных сценариев аварии с учетом их вероятности.

На следующем этапе исследования сложных технических систем, определяется вероятность аварии на опасном производственном объекте c формированием рассматриваемого поражающего фактора λ с использованием методов математической статистики, или логико-вероятностных методов, или методов экспертных оценок, рис. 7.

Рисунок 7. Методы определения частоты аварии на потенциально опасном объекте

Описанная выше процедура построения функции плотности распределения вероятностей массы аварийных выбросов для рассматриваемых сценариев возникновения аварии на объекте позволяет формализовать процесс возникновения и развития аварии на объекте, с учетом параметров модели истечения, частоты реализации и вероятности развития аварии.

На основе полученной функции f(M), вероятности аварии c формированием рассматриваемого поражающего фактора , а также полученной нами в работах [1; 2] функции вероятности поражения реципиента P(Г/М), определяется потенциальный риск R(E) поражения реципиента в рассматриваемой точке пространства при  условии аварийного выброса опасного вещества, рис. 8.

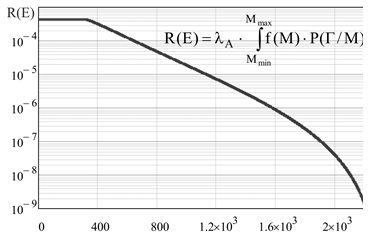
Рисунок 8. График потенциального риска

Вывод.

Предложенный подход к оценке риска возникновения и развития аварий в сложных технических системах на основе метода статистических испытаний Монте-Карло, позволяет в условиях объективно ограниченной исходной информации получить модель и параметры функции f(M) – плотности распределения аварийных выбросов на объекте и на ее основе определить потенциальный риск, характеризующий потенциальную опасность объекта.

Список литературы:

1. Козлитин А.М. Теория и методы анализа риска сложных технических систем: монография / А.М. Козлитин. Саратов: Сарат. гос. техн. ун-т, 2009. 200 с.

2. Козлитин А.М. Интегрированный риск техногенных систем. Теорети­ческие основы, методы анализа и количественной оценки: монография / Анатолий Козлитин. Saarbrücken: Palmarium Academic Publishing, 2012. 260 с.