МЕТОДИКА РАСЧЁТА КООРДИНАТ РАДИОТЕХНИЧЕСКОЙ СИСТЕМОЙ ОБНАРУЖЕНИЯ ПОЗИЦИЙ СТРЕЛКОВ

Статин Сергей Сергеевич

помощник ведущего инженера научно-исследовательского испытательного отдела
Государственного летно-испытательного центра Минобороны России им. В.П. Чкалова
РФ, г. Ахтубинск

E -mail: mr.stat@mail.ru

METHOD OF CALCULATION OF COORDINATES RADIO SYSTEM POSITION DETECTION SHOOTERS

Sergey Statin

Assistant chief engineer of research testing department of the State Flight Test Center Russian Ministry of Defense im. V .P. Chkalova
Russia, Akhtubinsk

АННОТАЦИЯ

Работа посвящена расчету угловых координат позиций стрелков при проведении испытаний акустической аппаратуры предупреждения об обстреле стрелковым оружием. Дан пример расчета угловых координат.

Библиографий – 3. Рисунков – 5.

ABSTRACT

The work is dedicated to the calculation of the angular coordinate positions shooters in tests of acoustic warning devices firing small arms. An example of calculating the angular coordinates.

Bibliographies – 3. Figures – 5.

Ключевые слова: звуковая разведка; вектор направления; полунатурная модель.

Keywords: sound intelligence; direction vector; HIL model.

Для определения местоположения звучащей цели в звуковой разведке используется принцип разности времен [3].

Для определения вектора направления на позицию стрелка в пространстве необходимо три приемника звукового сигнала. Вектор направления строится путем восстановления перпендикуляра к плоскости звуковой волны, определяемой по задержкам прихода сигнала на разные микрофоны (первый – второй и первый – третий).

Расположение микрофонов целесообразно выполнить в точках пространственной решетки на одинаковых расстояниях от центра координат для упрощения расчетов.

Общее количество микрофонов целесообразно выбрать таким образом, чтобы пространственная решетка из трех микрофонов была ориентирована в определенную часть пространства, разделенную полусферами относительно объекта установки (нижняя – верхняя полусфера, левая – правая полусфера, передняя – задняя полусфера). Таким образом, имеется 8 областей пространства по 3 микрофона в каждой. С учетом того, что каждый микрофон может использоваться в нескольких пространственных решетках и с учетом конструктивных возможностей объекта установки можно сделать вывод, что необходимо 10 микрофонов (рис. 1).

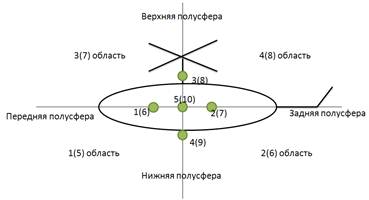
Рисунок 1. Расположение микрофонов в левой (правой) полусфере

Исходя из информации об очередности прихода сигнала на микрофоны, можно определить область и далее, по информации о задержках, определить вектор направления.

Для расчета угловых координат позиции стрелка использовалась полунатурная модель эксперимента (рис. 2).

Рисунок 2. Полунатурная модель эксперимента

Исходные данные для расчета:

V _зв – скорость звука (330 м/с);

V _пули – известная величина, характеризуемая типом оружия, определяемого при помощи спектрально-временного анализатора;

γ – угол при конусе маха, определяемый по формуле:

                                                                                                       (1)

L – база микрофонов, выбирается исходя из возможностей процессоров по обработке данных, для получения необходимой тактовой частоты обновления данных;

Δ t₁, Δt₂ – задержки прихода сигналов, вычисляются комплексом;

Н – высота объекта установки микрофонов, определяется штатным высотомером.

Необходимо определить: α – угол места, θ – азимут, D – дальность.

На рассматриваемой модели обозначены следующие точки и отрезки:

М ₁, М₂, М₃ – микрофоны;

N ₁, N₂ – точки на условной поверхности конуса Маха, определенные пересечением поверхности конуса и перпендикуляра к ней, проведенного из точек М₂, М₃;

О ₁, О₂ – точки на условной траектории движения пули, образованные пересечением ее с продолжением перпендикуляра к поверхности конуса Маха в точках N₁ и N₂;

Р ₁ – проекция точки М₁ на плоскость XOY;

Р ₂ – проекция точки О₂ на плоскость XOY;

Р ₃ – проекция точки N₂ на плоскость XOY;

Р ₄ – проекция точки О₁ на плоскость XOY;

Р ₅ – проекция точки N₁ на плоскость XOY;

О – начало координат;

М ₁М₂,М₁М₃– величины, равные ;

М ₂N₁ – расстояние, проходимое акустической волной за время Δt₁;

М ₃N₂ – расстояние, проходимое акустической волной за время Δt₂;

Рассмотрим прямоугольные треугольники М₂N₁М₁ и М₃N₂М₁.

                                                                   (2)

                                                                  (3)

Рассмотрим прямоугольные треугольники О₁N₁М₁ и О₂N₂М₁.

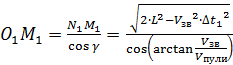                                                                                                             (4)

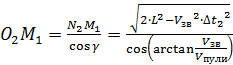                                                                                                          (5)

Угол α можно определить:

                                                                                                    (6)

                                                                                                (7)

Угол γ можно вычислить:

                                                                        (8)

                                                                     (9)

Далее определим Р₃Р₅ двумя способами:

                                                                        (10)

                                                                                                        (11)

Приравняв выражения (10) и (11), получим равенство:

                                                                  (12)

Рассмотрим прямоугольный треугольник ОР₃Р₁:

                                                        (13)

Из выражения (13) получим:

                                                                                            (14)

Поделим выражение (12) на (14) и получим:

                                                                                        (15)

Из выражения (15) получим θ:

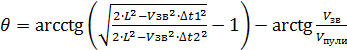                                                                   (16)

Из выражения (14) найдем α:

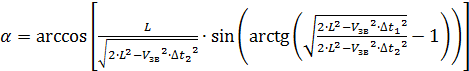                                                (17)

Дальность до позиции стрелка определяется по формуле:

                                                                                                 (18)

Определим погрешность измерения угловых координат [2].

Абсолютная погрешность измерения определяется выражением:

                                                        (19)

где: N – количество погрешностей;

i – номер погрешности;

 – погрешность;

Δ – результирующая погрешность.

Абсолютная погрешность измерения включает в себя:

 – погрешность измерения задержки сигнала Δt. Определяется тактовой частотой опроса вычислителя (рис. 3);

 – погрешность квантования уровня сигнала. Определяется характеристикой аналогово-цифрового преобразователя (рис. 3);

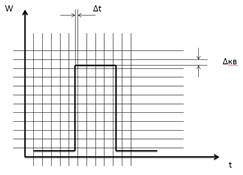
Рисунок 3. Погрешности  и

 – инструментальная погрешность средств измерений. Определена в паспорте на средство измерений;

 – погрешность округления. Определяется необходимой точностью получения результатов;

 – погрешность промаха, определяемая по формуле:

                                                      (20)

Данная погрешность имеет место из-за отсутствия информации о промахе, вносящей погрешность в определение направления на позицию стрелка (рис. 4).

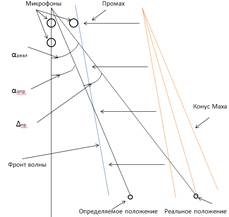
Рисунок 4. Погрешность промаха

Определение промаха поясняет рис.5. На рисунке обозначено:

D – расстояние от позиции стрелка до объекта;

N – промах.

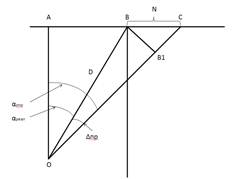
Рисунок 5. Определение промаха

Из рис. 5. следует, что при выполнении условия N<<D, погрешность промаха будет незначительной и ВВ₁≈N. Тогда, рассмотрев ΔОВВ₁, можно вычислить промах по формуле:

                                                          (21)

В процессе испытаний системы после получения большого числа многократных наблюдений проводится математическая статистическая обработка результатов измерений [1] и определяется СКО.

Необходимое количество наблюдений определяется из условия получения необходимого СКО:

                                                        (22)

Список литературы:
1. Геральд Крамер. Математические методы статистики. Под редакцией академика А.Н. Колмогорова. – 386 с.
2. Метрология и радиоизмерения: Учеб. Для вузов/ В.И. Нефедов, А.С. Сигов, В.К. Битюков и др.; Под ред. В.И. Нефедова. – 2-е изд., перераб. – М.: Высш. Шк., 2006. – 526 с.: ил.
3. Таланов А.В. Звуковая разведка артиллерии. Воениздат. Мин. ВС СССР. Москва. 1948 г. – 400 с.