РАЗРАБОТКА ПРИКЛАДНОГО АЛГОРИТМА ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ С БИНОМИНАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ

Магомедова Мадина Нурмагомедовна

аспирант
Санкт-Петербургского государственного экономического университета,
РФ, г. Санкт-Петербург

E-mail: 

DEVELOPMENT OF APPLICATION OF THE ALGORITHM OF STATISTICAL HYPOTHESIS TESTING WITH BINOMIAL DISTRIBUTION

Madina Magomedova

graduate
of Saint-Peteburg State university of economics branch in Kizlyar,
Russia, Saint-Peteburg

АННОТАЦИЯ

В статье рассматривается метод проверки статистических гипотез посредством структурного программирования. Представлена блок-схема алгоритма решения задачи. Унифицированы входные и выходные данные. Результатом является консольное приложение, реализованное в среде программирования.

ABSTRACT

The article discusses the method of statistical hypothesis testing through structural programming. Shows the block diagram of the algorithm of solving the problem. Unified input and output data. The result is a console application implemented in the programming environment.

Ключевые слова: программирование; алгоритм; математическая модель; блок-схема.

Keywords: programming; algorithm; modeling; diagram.

Данная работа носит комплексный характер, в большей степени содержит элементы исследования и разработки.

Цель работы: разработка алгоритма решения задачи проверки статистических гипотез с биноминальным распределением, а также реализация алгоритма на языке C++ в соответствии с основными этапами решения задачи на ЭВМ.

В качестве основы для разработки алгоритма, выбран метод структурного программирования.

Условие задачи: «Игральный кубик бросили 60 раз, при этом числа 1, 2, 3, 4, 5, 6 выпали соответственно 12, 9, 13, 11, 8, 7 раз. Можно ли на 5%-м уровне значимости отвергнуть гипотезу о симметричности кубика?»

Суть решение задачи заключается определении вероятности ошибки исходя из нулевой гипотезы. Рассмотрим данную гипотезу: ;

Определяем переменные, для решения этой гипотезы (Таб. 1):

Таблица 1.

Математические переменные нулевой гипотезы

, , , , ,

Вычисляем x2 (формула 1):

                                                                                                                                                                (1)

;

для

Для решения задачи были определены входные и выходные данные. В данном случае, при рассмотрении гипотезы, входными данными являются переменные: m1, m2, m3, m4, m5, m6.

При запуске программного модуля, необходимо ввести количество выпадений 1, 2, 3, 4, 5, и 6: m1=12, m2=9, m3=13, m4=11, m5=8 и m6=7 соответственно.

Результатом является переменная , далее гипотеза  принимает значение 2,8 отсюда вытекает сообщение следующего содержания:

«Гипотеза о симметричности кубика не может быть отвергнута, так как x2k>x2:\n».

Рисунок 1. Блок-схема алгоритма решения задачи

Далее представлен алгоритм на языке программирования С++.

{

int pn, m1,m2,m3,m4,m5,m6;

float x2, x2k ,k1, k2, k3, k4, k5, k6, a1, a2 ,a3 ,a4 ,a5 ,a6;

printf("Dokajem mojno li otvergnut gipotezy H0:p1=p2=1/6 o simmetrichnosti kybika, na 5-ti procentnom urovne znachimosti \n");

printf("Vvedite kolichestvo vipadeniy 1,2,3,4,5,6 :\n");

printf("vvedite m1:\n");

scanf("%d",&m1);

printf("vvedite m2:\n");

scanf("%d",&m2);

printf("vvedite m3:\n");

scanf("%d",&m3);

printf("vvedite m4:\n");

scanf("%d",&m4);

printf("vvedite m5:\n");

scanf("%d",&m5);

printf("vvedite m6:\n");

scanf("%d",&m6);

printf("vichislenie x2\n");

k1=(m1-np)*(m1-np);

a1=k1/np;

k2=(m2-np)*(m2-np);

a2=k2/np;

k3=(m3-np)*(m3-np);

a3=k3/np;

k4=(m4-np)*(m4-np);

a4=k4/np;

k5=(m5-np)*(m5-np);

a5=k5/np;

k6=(m6-np)*(m6-np);

a6=k6/np;

x2=a1+a2+a3+a4+a5+a6;

clrscr();

printf("x2=%f\n", x2);

if (x2k>x2);

{printf("Gipoteza o semmetrichnosti kybika ne mojit bit otvergnuta, tak kak x2k>x2:\n");}

else;

{printf("Gipoteza o simmetrichnosti kybika mojet bit otvergnuta, tak kak x2>x2k");}

getch(); }

В качестве средства тестирования допускается использование любого компилятора, поддерживающий язык C++.

После запуска программы появляется окно. В этом окне представляется сообщение о данной гипотезе и ввод переменных (Рисунок 2).

Рисунок 2. Сообщение о данной гипотезе и ввод переменных

Вводим все переменные, в соответствии с заданием, то есть

m1=12; m2=9; m3=13; m4=11; m5=8; m6=7.

Далее, следовательно, появляется окно с введенными переменными и окно с выводом результата проверки данной гипотезы (Рисунок 3–4).

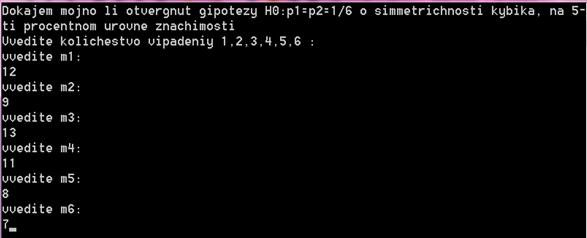
Рисунок 3. Окно с введенными переменными

Вывод результата проверки гипотезы H0 представлен на рисунке 4. Гипотеза не может быть отвергнута, так как выполняется необходимое условие.

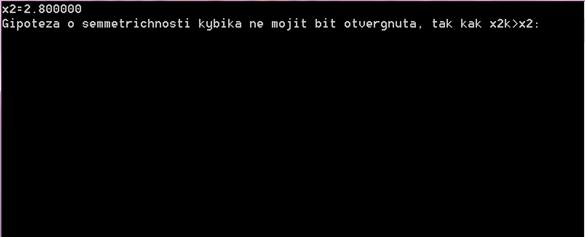
Рисунок 4. Вывод результата проверки гипотезы H0

В данной работе был представлен пример решения математической модели проверки статистических гипотез с биноминальным распределением [5] с использованием метода нулевой гипотезы, написан алгоритм на языке C++.

Список литературы:
1. Гаврилова И.В. Разработка приложений [Электронный ресурс]: учеб. пособие/ И.В. Гаврилова. - 2-е изд., стер. – М.: ФЛИНТА, 2012. – 241 c.
2. Дейл Н., Уимз Ч., Хедингтон М. Программирование на С++: Пер. с англ. – М.: ДМК Пресс. – 672 с.: ил.
3. Лавров С.С. Программирование. Математические основы, средства, теория. – СПб.: БХВ-Петербург, 2002. – 320 с.:ил.
4. Могилев А.В. Методы программирования. Компьютерные вычисления / А.В. Могилев, Л.В. Листрова. – СПб.: БХВ-Петербург, 2008. – 320 с.: ил.
5. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении: Учеб. Пособие. – 2-е изд., испр. – М.: Дело, 2002. – 440 с.