АЛГОРИТМ ДВУМЕРНОЙ УПАКОВКИ В КВАНТОВЫХ ВЫЧИСЛЕНИЯХ

Кухарчук Игорь Витальевич

ассистент кафедры электронных вычислительных машин

Белорусского государственного университета информатики и радиоэлектроники,

Республика Беларусь, г. Минск

E -mail: ihar.kukharchuk@gmail.com

ALGORITHM OF A TWO-DIMENSIONAL PACKING IN QUANTUM COMPUTING

Ihar Kukharchuk

assistant Professor at the Department of Electronic Computing Machines,

Belarussian State University of Informatics and Radioelectronics,

Republic of Belarus, Minsk

АННОТАЦИЯ

Среда разработки для квантовых вычислений не обладает широким набором реализованных алгоритмов. Целью является расширение прикладной библиотеки квантовых алгоритмов путём адаптации общей модели классического алгоритма двумерной упаковки. Для достижения поставленной цели были использованы методы обобщения классических алгоритмов и дедукция для построения квантового. В результате представленный алгоритм может быть использован на существующем квантовом сопроцессоре. Данная реализация позволяет расширить ареал квантовых алгоритмов в области задач теории сложности вычислений.

ABSTRACT

Software development environment for quantum computing has not a wide range of implemented algorithms. The aim is to expand the library of quantum algorithms by adapting a common structure of two-dimensional packaging algorithm. To achieve this goal I have been used methods of generalization for classical algorithms and the deduction for the quantum part solution. As a result, presented algorithm can be used on existing quantum coprocessor. This implementation allows expanding the area of quantum algorithms in problems of the theory of computational complexity.

Ключевые слова: квантовые вычисления; алгоритм Гровера; задача двумерной упаковки.

Keywords: quantum computations; Grover’s algorithm; two-dimension packaging problem.

Современный мир предоставляет жёсткие требования по срокам обработки информации. Классический компьютер перестаёт удовлетворять этим требованиям. На смену текущей модели вычислительного процесса приходят квантовые компьютеры, способные решать задачи экспоненциальной сложности за полиномиальное время. Одна из таких задач – задача о двумерной упаковке в контейнер – будет рассмотрена данной статьёй.

Решение о рассмотрении данной задачи исходит из того, что область квантовых вычислений перешла в стадию интенсивного развития совсем недавно. Технологии на этапе становления обладают рядом известных проблем. Одной из таких проблем является недостаток реализованных под данную модель алгоритмов. Дело в том, что классические алгоритмы не могут быть использованы в их текущем описательном характере на квантовых сопроцессорах. Это приводит к тому, что необходимо вводить дополнительный этап трансляции или адаптации существующего алгоритма на квантовую модель вычислений. Также стоит учитывать, что не каждый алгоритм способен быть перенесён из классической модели с сохранением или улучшением показателей производительности.

В рамках данной работы были рассмотрены существующие алгоритмы двумерной упаковки и построена модель подобного алгоритма для квантовых вычислений.

Приведём определение задачи двумерной упаковки в контейнеры в общем виде. Дано n прямоугольных предметов с размерамии неограниченное количество одинаковых контейнеров размером . Задача двумерной упаковки в контейнеры состоит в том, чтобы минимизировать число требуемых контейнеров, в которые будут упакованы все предметы без перекрытия(1) [2, с. 96]:

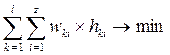                                           (1)

где: w, h – ширина и высота одного из предметов;

k, z – номер контейнера и прямоугольника соответственно.

В формуле (1) первой является сумма для контейнеров количеством l, вторая для прямоугольников, находящихся в контейнере k. Для упрощения построения примем, что имеется лишь один контейнер для упаковки, следовательно минимизировать необходимо высоту уложенных в один контейнер прямоугольников. Тогда формула станет выглядеть следующим образом:

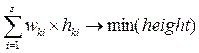                                     (2)

где: w, h – ширина и высота одного из предметов;

z – номер прямоугольника соответственно.

В формуле (2) количество всех прямоугольников ограничено числом z, а минимизируется конечная высота в прямоугольнике. В таком случае необходимо вывести общую формулу оценки производительности алгоритма для конкретного контейнера [3, с. 325]:

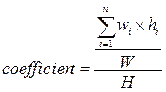                                            (3)

где: w, h – ширина и высота одного из предметов;

W, H – ширина и высота контейнера соответственно.

В формуле (3) в числителе числителя находится сумма площадей всех прямоугольников, которая затем делится на ширину контейнера. Из данного выражения получаем оптимальное расположение прямоугольников плотным слоем, что чаще всего недостижимо. Полученное отношение делим на высоту контейнера, занятую прямоугольниками расположенными квантовым алгоритмом. Данный коэффициент отражает степень приближенности к идеальному варианту в процентном соотношении.

Существует два наиболее распространённых типа алгоритмов двумерной упаковки: online и offline. Первые из них подразумевают, что у вас нет конечного набора прямоугольников непосредственно в момент расположения их в контейнере, во втором же случае вы обладаете полным набором, который необходимо упаковать. Разработанный квантовый алгоритм относится к типу offline.

В общем виде последовательность действий алгоритма состоит из следующих этапов:

·     подготовка и инициализация входных данных

·     воздействие оракула

·     воздействие гейта диффузии

·     копирование полученного решения

·     измерение отобранного состояния

Рассмотрим данные этапы подробнее. Входными данными являются прямоугольники со значениями их высоты и ширины. Необходимо на каждом уровне максимизировать заполняемость. Одним из классических алгоритмов, который кроме конечного результата на каждой итерации, возвращают отобранный набор, является knapsack 0-1. Именно он служит прототипом квантового алгоритма. Для приведения набора параметров прямоугольников к качественному виду находятся площади каждого прямоугольника, так как этот показатель будет основным критерием выбора конкретного набора.

Квантовый алгоритм поиска способен работать лишь с бинарными данными, поэтому существует необходимость построения таблицы соответствия, которая для двух прямоугольников отражена в таблице 1.

Таблица 1 отражает, что в первом векторе данных набора не будет отражена ни площадь первого прямоугольника, ни площадь второго, во втором векторе будет учтена площадь второго, в четвертом – обоих. Таким же образом таблица соответствия масштабируется для большего количества прямоугольников.

Таблица 1.

Таблица соответствия для входных данных

Рассмотрим квантовый оракул, построенный на основе алгоритма Гровера. В данном случае оракул должен инвертировать фазу искомого значения, а это значит, что на выходе будет получено значение [3, с. 155]. Этим и обусловлено текущее представление: .

Гейт диффузии предназначен для отражения кубитов относительно среднего значения. Одно из возможных реализации данного действия было выбрано для рассматриваемого алгоритма. В данном случае гейт будет выглядеть следующим образом:

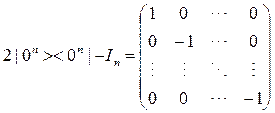                               (4)

На выходе гейта диффузии имеется частичное решение: набор отобранных прямоугольников для расположения их на определенном уровне. Здесь в алгоритме предусмотрена операция копирования вектора кубитов до операции измерения. Делается это с целью исключить отобранный набор из общего квантового пространства наборов без операции измерения, что позволит сэкономить на повторении операций инициализации перед оракулом.

Первоначальный вектор отправляется на операцию измерения, а затем на верификацию, которая покажет, способны ли уложиться данные прямоугольники на уровень предложенной высоты. Функция верификации на начальном этапе может принимать простейший вид: процентное отношение заполненного пространства не должно превышать показателя от возможной площади. Конечно, таким образом не гарантируется на 100% возможность расположения прямоугольников в контейнере, однако этого достаточно для проведения дальнейших расчетов.

Схема для данного алгоритма отражена на рисунке 1.

Рисунок 1. Квантовая схема алгоритма

Обратная связь на рисунке 1 отображена для наглядности, на реальной квантовой схеме такое действие разворачивается в длинную последовательную цепочку подобных операторов.

Необходимо определить, какое количество раз будет запускаться над каждым набором процесс квантового поиска. В прикладной модели это достигается путем анализа результатов тестирования. Проблема в том, что на выходе алгоритма поиска Гровера нельзя гарантировать, что полученный результат является истинным. Поэтому алгоритм запускается конечное количество раз и производится оценка полученных данных для выбора значения получения наиболее достоверного результата. Результаты тестирования для сотни запусков отражены на рисунке 2.

Рисунок 2. Результаты тестирования алгоритма поиска Гровера

Таким образом достаточно выполнить квантовый поиск 13 раз чтобы получить вероятность результата около 95 %. В итоге общая сложность алгоритма окажется  при худшем сценарии.

На рисунке 3 отражены затраты по времени для количества прямоугольников от 1 до 40, размещаемых в контейнере. Справочное значение сложности в худшем случае для алгоритма NFDN составляет .

Рисунок 3. Результаты времени работы оцениваемых алгоритмов

Справочное значение лучшего по степени упаковки классического алгоритма FCNR по сложности составляет  в худшем случае. Сравнение происходит с классическим и квантовым вариантом реализации knapsack0-1. Как можно заметить, классическую реализацию knapsack совершенно не выгодно использовать в случае наличия более чем 35 прямоугольников.

На рисунке 4 отражены результаты запусков лучшего по степени упаковки FCNR, наиболее простого NFDN и квантовой версии алгоритма knapsack0-1. Классический knapsack не приводится, так как его результат практически идентичен результату квантового алгоритма.

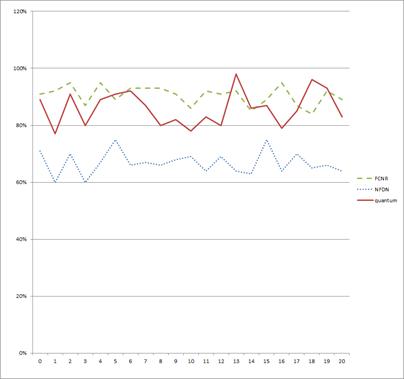
Рисунок 4. Результаты степени упаковки оцениваемых алгоритмов

Формируя вывод на основе полученных данных получаем, что отношение скорости к качеству упаковки у квантового алгоритма значительно выше, что делает его конкурентоспособным в данной области задач. Однако следует учитывать и основной недостаток квантового алгоритма: результат работы есть список предложенных к упаковке на каждом уровне прямоугольников, но не их расположение. А это свидетельствует о том, что будет необходимо затратить дополнительные вычислительные ресурсы на то, чтобы расположить их в контейнере.

В результате проведенного исследования была разработана и реализована квантовая модель алгоритма теории сложности – двумерная упаковка в контейнеры.

Список литературы:
1. Душкин Р.В. Квантовые вычисления и функциональное программирование. – М.: Проспект, 2014. – С. 150–163.
2. Barnes F.W. Packing the Maximum Number of m x n Tiles in a Large p x q Rectangle. – ORS, 2007. – P. 93–100.
3. Martello S. Optimal and Canonical Solutions of the Change Making Problem // European Journal of Operational Research. – 1999. – Vol. 4. – P. 322–329.