ГРАВИМЕТРИЧЕСКАЯ  МОДЕЛЬ  ГЕОИДА  НА  ТЕРРИТОРИЮ  КАРАГАНДИНСКОЙ  ОБЛАСТИ,  КАЗАХСТАН

Шоганбекова  Дания  Асыгатовна

PhD  докторант, 
Казахского  национального  исследовательского  технического  университета  имени  К.И.  Сатпаева, 
Республика  Казахстан,  г.  Алматы

E-mail: 

GRAVIMETRIC  GEOID  MODEL  OVER  TERRITORY  OF  KARAGANDA  REGION,  KAZAKHSTAN

Daniya  Shoganbekova

PhD  student 
of  the  Kazakh  National  Technical  Research  university

named  of  K.I.  Satpayev, 
Republic  of  Kazakhstan,  Almaty

АННОТАЦИЯ

Представлены  результаты  вычисления  и  3D  моделирования  локальной  гравиметрической  модели  геоида  Карагандинской  области  Республики  Казахстан.  Модель  гравиметрического  геоида  рассчитана  по  сетке  5'  x  5'  с  использованием  наземных  гравиметрических  пунктов.  Длинноволновые  компоненты  модели  геоида  определены  по  данным  геопотенциала  глобальной  гравитационной  модели  EIGEN-6C4,  а  коротковолновые  –  из  наземных  гравиметрических  измерений  по  модифицированной  формуле  Стокса.  Оценка  точности  показала,  что  среднеквадратическая  ошибка  определения  абсолютных  значений  высот  геоида  составляет  10  см. 

ABSTRACT

The  results  of  the  calculations  and  3D  simulation  of  the  local  gravimetric  geoid  model  of  the  Karaganda  region  of  Kazakhstan  are  given.  Gravimetric  geoid  model  is  modelled  on  a  grid  5  'x  5'  by  using  terrestrial  gravity  points.  The  long-wavelength  components  of  the  geoid  model  determined  according  to  the  gravity  of  the  global  geopotential  model  EIGEN-6C4,  and  shortwave  –  from  land-based  gravity  measurements  using  a  modified  Stokes  formula.  Accuracy  estimation  showed  that  the  mean  square  error  in  determining  the  absolute  values  of  the  geoid  height  is  10  cm.

Ключевые  слова:  геоид;  модификация  формулы  Стокса;  Караганда.

Keywords:  geoid;  modification  of  Stokes  formula;  Karaganda.

Введение.  На  сегодняшний  день  замена  геометрического  нивелирования  методом  определения  нормальных  высот  по  геодезическим  высотам,  полученных  из  спутниковых  измерений,  является  одной  из  наиболее  актуальных  задач,  стоящих  перед  геодезическим  производством.  Решение  данной  задачи  сводится  к  использованию  модели  высот  геоида  над  эллипсоидом  WGS–84.  Преобразование  геодезических  высот  в  нормальные  можно  выразить  через  известную  формулу  [6]:

  (1)

где:    нормальная  высота;

  геодезическая  высота; 

  высота  геоида  над  эллипсоидом.

По  определению,  геоид  представляет  собой  эквипотенциальную  (уровенную)  поверхность  гравитационного  геопотенциала,  совпадающую  с  поверхностью  Мирового  океана  в  невозмущенном  состоянии.

Данная  статья  посвящена  результатам  построения  модели  высот  гравиметрического  геоида,  которая  могла  бы  быть  распространена  на  территорию  Карагандинской  области,  и  по  точности  могла  бы  достигать  уровня,  сопостовимого  с  точностью  геометрического  нивелирования  III–IV  классов. 

Методы  исследования.  Для  расчета  модели  гравиметрического  геоида  была  выбрана  техника  модификации  формулы  Стокса  методом  наименьших  квадратов,  так  как  он  оптимальным  образом  сочетает  в  себе  различные  наборы  данных.  Кроме  того,  данный  метод  позволяет  использовать  добавочные  поправки  за  рельеф,  продолжение  вниз,  атмосферу  и  эллипсоидальную  форму  Земли. 

Теоретические  и  практические  аспекты  используемого  метода  главным  образом  были  разработаны  профессором  Ларс  Съебергом  с  1984  года  [7].  Этот  метод  оказался  наиболее  подходящим  для  точного  определения  модели  гравиметрического  геоида  [5].  Техника  модификации  формулы  Стокса  методом  наименьших  квадратов  также  известна  под  название  КТН-метод  (Kungliga  Tekniska  högskolan).  КТН-метод  дает  хорошие  результаты  в  связи  с  известным  потенциалом  ядра  модификации  методом  наименьших  квадратов,  которое  оптимальным  способом  исправляет  ошибки  наземных  гравиметрических  данных,  ошибки  глобальных  гравиметрических  моделей  и  погрешности  сокращения.  С  практической  точки  зрения,  с  использованием  точных  условий  добавочных  поправок,  КТН-метод  является  точным,  простым  и  вычислительно-эффективным.

Исходные  данные.  Карагандинская  область  расположена  на  территории  Республики  Казахстан,  между  45  и  52  градусами  северной  широты  и  62  и  77  градусами  восточной  долготы  (Рисунок  1). 

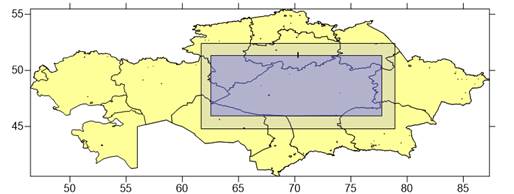
Рисунок  1.  Расположение  исследуемой  территории  (выделено  жирным  прямоугольником).  Граница  внешнего  отступления  на  фиксированном  сферическом  расстоянии

Для  вычисления  гравиметрической  модели  геоида  с    на  территорию  Карагандинской  области  необходим  следующий  набор  данных:

·     Наземные  гравиметрические  данные.  Для  данного  исследования  была  использована  карта  гравиметрической  съемки,  выполненная  на  всю  территорию  Республики  в  масштабе  1:200000.  Ошибки  интерполяции  аномалий  в  свободном  воздухе  в  сетку  с  разрешением  5'x5'  между  гравиметрическими  пунктами  не  превышают  0,6  мГал.

·     Цифровая  модель  рельефа  SRTM  (Shuttle  Radar  Topography  Mission).  Средние  квадратические  ошибки  высот  SRTM  оцениваются  величинами  2–10  м; 

·     Глобальная  гравитационная  модель  EIGEN-6C4  –  комбинированная  глобальная  гравитационная  модель  (ГГМ),  которая  сочетает  в  себе  данные  GOCE,  GRACE,  Lageos  и  наземные  гравиметрические  данные  и  данные  альтиметрии  [2;  3];

·     Точки  GPS/Нивелирования  для  оценки  точности  –  35  точек,  расположенные  на  участке  исследования,  с  известными  ортометрической  и  нормальной  высотами; 

Предварительные  вычисления  и  подготовка  данных  подробнее  описана  в  работах  Д.  Шоганбековой  [2;  3].

Построение  гравиметрической  модели  высот  геоида. 

Расчет  предварительной  модели  высот  геоида.  Для  повышения  эффиктивности  вычисления  и  визуализации  промежуточных  данных  вычисления  процедуру  моделирования  предварительной  модели  высот  геоида  можно  разделить  на  3  этапа:

1.  вычисление  коротковолнового  компонента  модели    по  наземным  гравиметрическим  данным  (Рисунок  2);

2.  вычисление  длинноволнового  компонента  по  данным  Глобальной  гравитационной  модели  (Рисунок  2);

3.  объединение  двух  компонентов  в  предварительную  модель  геоида  (Рисунок  3);.

Рисунок  3.  Результаты  моделирования  компонентов  гравиметрического  геоида

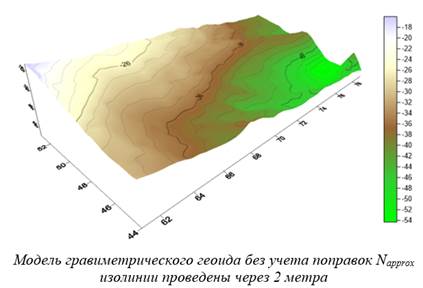
Рисунок  4.  Построение  модели  грвиметрического  геоида  без  учета  поправок

Поправочные  коэффициенты  для  предварительной  модели  гравиметрического  геоида.  Все  поправочные  коэффициенты  были  вычислены  согласно  методу  КТИ  [7].  Результаты  вычисления  представлены  на  рисунке  4.  Окончательная  модель  геоида  была  получена  путем  введения  всех  полученных  поправок  в  предварительную  модель.  Полученная  модель  представлена  на  рисунке  5.

Оценка  точности.  Для  оценки  возможности  применения  созданной  модели  KarGM2015.  В  геодезической  практике  были  использованы  материалы  экспериментального  хода  спутникового  нивелирования  [3].  В  ходе  этой  работы  были  выполнены  спутниковые  измерения  на  пунктах  линии  нивелирования  I  класса  длиной  около  300  км. 

В  ходе  проверки  модели  линия  спутникового  нивелирования  была  разбита  на  участки  протяженностью  примерно    Пункты  нивелирования,  попавшие  на  границы  участков,  были  выбраны  в  качестве  исходных  пунктов  спутникового  нивелирования,  отметки  нормальных  высот  которых  полагались  известными  и  безошибочными.  Нормальные  высоты  остальных  пунктов  полагались  подлежащими  определению.

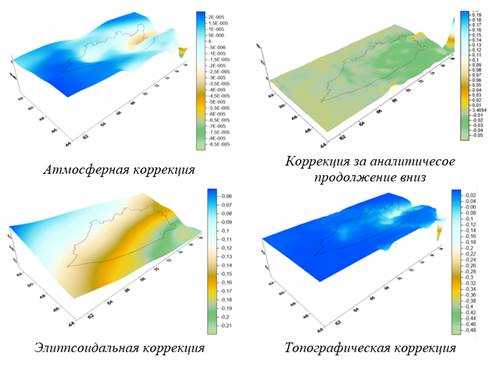
Рисунок  5.  Учет  поправочных  коэффициентов

Рисунок  6.  Гравиметрическая  модель  геоида  на  территорию  Карагандинской  области  изолинии  проведены  через  1  метр

На  первом  этапе  для  всех  пунктов  были  вычислены  значения  нормальных  высот  как  разность  геодезических  высот,  полученных  по  спутниковым  измерениям,  и  высот  геоида,  полученных  по  модели.  На  втором  этапе  для  пунктов,  выбранных  в  качестве  исходных,  были  получены  невязки  между  значениями  нормальных  высот,  известных  из  нивелирования  I  класса,  и  вычисленными  значениями  нормальных  высот  [3].  Окончательные  отметки  нормальных  высот  были  получены  после  распределения  невязок  на  все  пункты  хода  спутникового  нивелирования.  Невязки  распределялись  линейно,  пропорционально  расстоянию  от  исходных  пунктов.

В  результате  для  всех  пунктов  были  вычислены  ошибки  определения  нормальных  высот  как  разности  между  значениями  нормальных  высот,  полученными  с  помощью  модели  высот  геоида,  и  эталонными  значениями.  Ошибки  представлены  на  рисунке  7.  Для  наглядности  на  рисунке  5  также  показаны  значения  ожидаемых  среднеквадратических  ошибок  нивелирования  III  класса  [4].

Рисунок  7.  Ошибки  определениянормальных  высот

Только  для  одного  пункта  полученная  ошибка  превысила  среднеквадратическую  ошибку  нивелирования  III  класса  больше  чем  в  3  раза.  Этот  пункт  расположен  на  расстоянии  около  100  м  от  исходного  пункта.  Поэтому  величина  0,057  м  для  него  оказалась  недопустимой.  Для  остальных  пунктов  разности  между  вычисленными  значениями  и  эталонными  значениями  нормальных  высот  не  превышают  допустимых  требований,  предъявляемых  к  нивелированию  III  класса.  Для  большинства  пунктов  полученные  ошибки  не  превысили  значений  среднеквадратических  ошибок  нивелирования  III  класса  [1].  Среднеквадратическое  значение  из  всех  ошибок,  полученных  в  результате  сравнения,  составило  0,037  м.

Заключение.  Результатом  проведенной  исследовательской  работы  является  построенная  модель  гравиметрического  геоида  разрешением  ,  названная  моделью  КаrGM2014.

Выполнены  исследования  точности  созданной  модели  высот  геоида.  Полученные  оценки  показали,  что  среднеквадратическаяошибка  определения  абсолютных  значений  высот  геоидасоставляет  10  см.  Точность  определения  превышений  высот  геоида  позволяет  использовать  модель  для  выполнения  спутникового  нивелирования,  сопоставимого  по  точности  с  геометрическим  нивелированием  3–4  классов.

Теория,  описанная  в  данной  исследовательской  работе  является  первым  шагом  на  пути  к  реализации  модели  геоида  Республики  Казахстан  с  точностью  до  1  сантиметра.

Список  литературы:

1. Мориц  Г.  Современная  физическая  геодезия.  Пер.  с  англ.  –  М.:  Недра,  1983.  –  392  с.
2. Шоганбекова  Д.А.,  Кабасов  Р.Р.  Выбор  оптимальной  модели  гравиметрического  поля  Земли  для  вычисления  высот  геоида  на  территорию  Мангыстауской  области  //  Вестник  КазГАСА.  –  2013.  –  №  2(48).  –  с.  203–206.
3. Шоганбекова  Д.А.,  Кабасов  Р.Р.,  Современное  состояние  моделей  гравитационного  поля  Земли  //  Инновационные  и  наукоемкие  технологии  в  строительной  индустрии.  Международная  научно-практическая  конференция  (Алматы,  6  апреля  2013  г.)  –  Аламты,  2013.  –  С.  144–147.
4. Ditmar  P.,  Kusche  J.,  and  Klees  R.,  Computation  of  spherical  harmonic  coefficients  from  gravity  gradiometry  data  to  be  acquired  by  the  GOCE  satellite:  regularisation  issues  //  Journal  of  Geodesy.  2003,  Volume  77.  –  Р.  465–477.
5. Ellmann  A.  The  geoid  model  for  the  Baltic  countries  determined  by  the  least  squares  modification  of  Stokes'  formula:  Doctoral  dissertation  in  Geodesy.  –  KTH.,  2004.  –  96  р.
6. Shoganbekova  D.  Determination  of  a  gravimetric  geoid  model  of  Kazakhstan  using  the  KTH-method:  Master  thesis  –  KTH.,  2010.  –  67  р.
7. Sjöberg  L.A.  General  model  of  modifying  Stokes’  formula  and  its  least  squares  solution  //  Journal  of  Geodesy.  –  2003,  –  Volume  77,  –  P.  459–464.