МАТЕМАТИЧЕСКАЯ  МОДЕЛЬ  СИСТЕМЫ  АКТИВНОГО  ПОДАВЛЕНИЯ  СЛУЧАЙНОГО  НИЗКОЧАСТОТНОГО  ШУМА

Ушенина  Инна  Владимировна

канд.  техн.  наук, 
ПензГТУ, 
РФ,  г.  Пенза

E-mail: 

MATHEMATICAL  MODEL  OF  AN  ACTIVE  NOISE  CONTROL  SYSTEM  WORKING  WITH  BANDLIMITED  RANDOM  NOISE

Inna  Ushenina

candidate  of  science, 
PenzSTU, 
Russia,  Penza

Исследование  выполнено  при  финансовой  поддержке  РФФИ  в  рамках  научного  проекта  №14-07-31091  мол_а

АННОТАЦИЯ

В  работе  рассматривается  математическая  модель  системы  активного  подавления  акустического  шума,  разработанная  в  MATLAB.  Модель  предназначена  для  выявления  характера  зависимости  уровня  подавления  случайного  низкочастотного  шума  от  порядка  адаптивного  фильтра  системы.

ABSTRACT

This  paper  considers  a  MATLAB  model  of  an  active  noise  control  system.  This  model  is  intended  to  recognize  a  dependence  character  of  noise  suppression  level  on  the  order  of  the  system’s  adaptive  filter.

Ключевые  слова:  активное  подавление  шума;  математическая  модель;  адаптивный  фильтр.

Keywords:  active  noise  control;  mathematical  model;  adaptive  filter.

Принцип  действия  большинства  систем  активного  подавления  акустического  шума  (АПШ)  состоит  в  формировании  противофазного  компенсирующего  сигнала  на  основе  анализа  опорного  сигнала  и  сигнала  ошибки,  являющегося  разностью  шума  и  компенсирующего  сигнала  в  контрольной  точке  (рисунок  1).  Эту  задачу,  как  правило,  выполняет  адаптивный  фильтр  (АФ)  с  алгоритмом  наименьших  средних  квадратов  и  предварительной  фильтрацией  опорного  сигнала  [2;  4;  5].

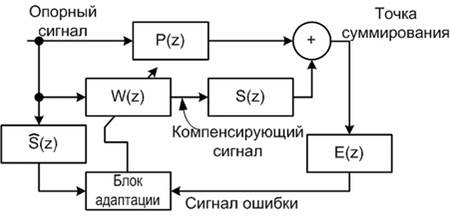
Рисунок  1.  Структура  системы  АПШ  с  опорным  сигналом

На  рисунке  1  P(z)  –  передаточная  функция  акустического  пути  распространения  шума  от  опорного  микрофона  до  точки  суммирования;  W(z)  –  передаточная  функция  АФ;  S(z)  –  передаточная  функция  пути  компенсации,  включающего  динамик  –  от  выхода  АФ  до  точки  суммирования;  E(z)  –  передаточная  функция  пути  сигнала  ошибки,  включающего  микрофон  ошибки  –  от  точки  суммирования  до  входа  блока  адаптации;  Ŝ(z)  –  оценка  S(z)E(z),  используемая  для  предварительной  фильтрации  опорного  сигнала  [5]. 

Оптимальной  передаточной  функцией  АФ  является  (1):

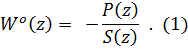
Поскольку  инверсия  S(z),  как  правило,  имеет  бесконечную  импульсную  характеристику  (ИХ),  выбор  порядка  (количества  коэффициентов  N)  АФ  путем  приравнивания  к  длине  ИХ  идентифицируемой  системы  [3]  невозможен.

Если  подавляемый  шум  содержит  одну  или  несколько  гармоник,  N  принято  определять  из  расчета  4–20  коэффициентов  на  гармонику.  Для  системы,  работающей  со  случайным  шумом,  процедура  выбора  N  не  формализована  [8]. 

Тем  не  менее,  выбор  порядка  АФ  является  важным  этапом  разработки  системы  АПШ.  С  одной  стороны,  от  N  зависит  достижимый  уровень  подавления  шума  и  скорость  сходимости  алгоритма  [3].  С  другой  стороны,  с  повышением  N  увеличивается  объем  ресурсов,  требуемых  на  реализацию  адаптивного  алгоритма,  что  актуально  для  многоканальных  систем  АПШ  [2;  5]. 

В  данной  работе  рассматривается  MATLAB-модель  системы  АПШ,  предназначенная  для  выявления  характера  зависимости  уровня  подавления  шума  от  порядка  АФ,  что  способствует  выбору  наименьшего  порядка  АФ,  позволяющего  получить  требуемый  уровень  подавления.

При  создании  модели  предполагаются  известными:  передаточные  функции  и  задержки  акустического  пути  распространения  шума  и  пути  компенсации,  которые  могут  быть  получены  в  результате  измерений  [7]  или  идентификации  [2;  4;  5],  характеристики  шума,  частота  дискретизации  системы  АПШ,  шаг  сходимости  [1]  и  количество  итераций  адаптивного  алгоритма.  Для  моделирования  АФ  используется  функция  MATLAB  adaptfilt.filtxlms  [6].

Модель  создавалась  с  соблюдением  условия  каузальности  [2;  4;  5]:  задержка  акустического  пути  устанавливалась  не  меньшей,  чем  задержка  пути  компенсации.  Также  было  принято  допущение  об  отсутствии  акустической  обратной  связи  [4]  между  опорным  микрофоном  и  микрофоном  ошибки.

Для  получения  зависимости  уровня  подавления  шума  A  от  N  задан  набор  из  J  значений  N_j,  для  которого  в  виде  цикла  организуется  моделирование  АФ.  Результатом  каждого  j-го  выполнения  операций  цикла  является  уровень  подавления  шума  A_j,  рассчитанный  по  формуле  (2):

  ,  (2)

где:  P_xj  –  средняя  мощность  опорного  сигнала  при  N=N_j; 

P_ej  –  средняя  мощность  сигнала  ошибки  при  N=N_j.  Для  расчета  P_ej  берутся  отсчеты  сигнала  ошибки,  полученные  после  завершения  процесса  сходимости. 

Рассмотрим  для  примера  результаты,  полученные  при  использовании  в  качестве  моделей  P(z)  и  S(z)  КИХ-фильтров  с  экспоненциальным  затуханием  огибающей  ИХ,  часто  встречающимся  на  практике  [3].  ИХ  модели  S(z)  представлена  на  рисунке  2.  ИХ  модели  P(z)  аналогична  представленной  на  рисунке  2,  но  имеет  большую  задержку.

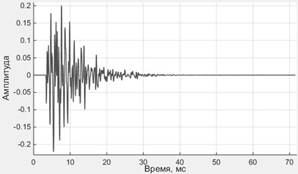
Рисунок  2.  ИХ  модели  S(z),  с  экспоненциальным  затуханием  огибающей

В  качестве  модели  опорного  сигнала  использовался  случайный  шум  с  диапазоном  частот  100–1500  Гц.  Частота  дискретизации  системы  АПШ,  которая  оптимально  должна  быть  в  10–20  раз  выше  частот  подавляемого  шума  [4;  8],  выбрана  равной  15  кГц.  Шаг  сходимости  адаптивного  алгоритма  выбран  достаточно  малым,  чтобы  обеспечить  сходимость  даже  для  АФ  высоких  порядков,  и  составляет  0,0005.  Порядок  АФ  варьировался  от  200  до  2000  коэффициентов.  Сигнал  ошибки  оценивался  спустя  3·10⁶  итераций  адаптивного  алгоритма.

На  рисунке  3  представлены  полученные  в  результате  моделирования  графики  зависимости  A  от  N  при  различных  соотношениях  задержек  P(z)  и  S(z).  Задержка  P(z)  для  всех  случаев  принималась  равной  50  отсчетам;  задержка  S(z)  –  от  10  до  55  отсчетов  –  указана  рядом  с  каждым  из  графиков.

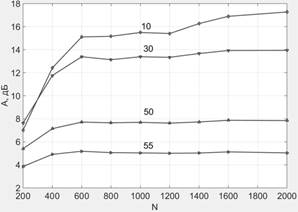
Рисунок  3.  Зависимость  уровня  подавления  шума  A  от  порядка  АФ  N  для  различных  соотношений  задержек  P(z)  и  S(z)

Модель  системы  АПШ  позволяет  также  отследить  приближение  к  характеристикам  акустического  пути,  достигаемое  последовательно  соединенными  W(z)  и  S(z)  при  различных  N  и  других  параметрах  системы.  Приближения  к  АЧХ  и  групповой  задержке  акустического  пути  при  N  =  400  и  N=1400,  и  задержке  пути  компенсации  на  10  отсчетов  представлены  на  рисунках  4  и  5  соответственно. 

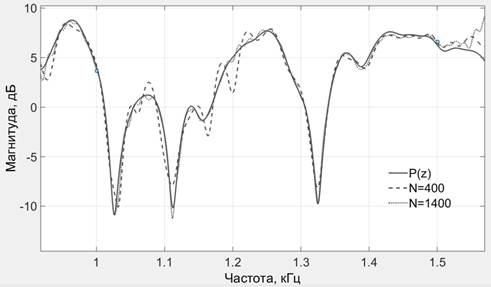
Рисунок  4.  АЧХ  P(z)  и  последовательно  соединенных  W(z)  и  S(z)  для  двух  значений  N  (фрагмент  рабочего  диапазона  частот)

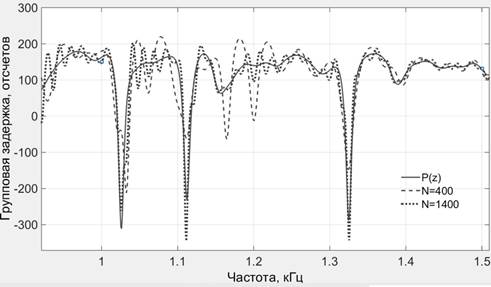
Рисунок  5.  Групповые  задержки  P(z)  и  последовательно  соединенных  W(z)  и  S(z)  для  двух  значений  N  (фрагмент  рабочего  диапазона  частот)

Согласно  рисункам  3–5,  при  соблюдении  условия  каузальности  уровень  подавления  шума  повышается  с  увеличением  порядка  АФ.  Однако  для  N  более  600  коэффициентов  рост  A  замедляется.  Задержка  S(z)  в  значительной  степени  влияет  на  достижимый  уровень  подавления  шума.  Наилучшее  приближение  к  характеристикам  P(z)  достигается  на  частотах,  приблизительно  в  10  раз  меньших  частоты  дискретизации  системы.

Таким  образом,  предложенная  модель  системы  АПШ  позволяет  оценить  характер  зависимости  уровня  подавления  шума  от  порядка  АФ  для  заданных  параметров  шума  и  системы,  и  выбрать  минимальный  порядок  АФ,  обеспечивающий  требования  к  уровню  подавления  шума.

Список  литературы:

1. Джиган  В.И.  Адаптивная  фильтрация  сигналов:  теория  и  алгоритмы.  М.:  Техносфера,  2013.  –  528  с.
2. Elliott  S.  Signal  processing  for  active  control.  Academic  Press,  2000. 
3. Gu  Y.  et  al.  Convergence  analysis  of  a  deficient-length  LMS  filter  and  optimal-length  sequence  to  model  exponential  decay  impulse  response  //Signal  Processing  Letters,  IEEE.  –  2003.  –  Т.  10.  –  №  1.  –  С.  4–7.
4. Hansen  C.H.  et  al.  Active  control  of  noise  and  vibration.  –  2nd  ed.  CRC  Press,  2013.
5. Kuo  S.M.,  Morgan  D.R.  Active  noise  control  system  algorithms  and  DSP  implementations.  John  Wiley  &  Sons,  1996. 
6. MathWorks  documentation.  FIR  adaptive  filter  that  uses  filtered-x  LMS  algorithm.  [Электронный  ресурс]  –  Режим  доступа.  –  URL:  http://www.mathworks.com/help/dsp/ref/adaptfilt.filtxlms.html?s_tid=srchtitle  (дата  обращения  15.11.2015).
7. Morgan  D.R.,  Quinlan  D.A.  Local  silencing  of  room  acoustic  noise  using  broadband  active  noise  control  //Applications  of  Signal  Processing  to  Audio  and  Acoustics,  1993.  Final  Program  and  Paper  Summaries.,  1993  IEEE  Workshop  on.  –  IEEE,  1993.  –  С.  23–25.
8. Snyder  S.D.  Active  noise  control  primer.  Springer,  2000.