ПРОГНОЗИРОВАНИЕ  ОСТАТОЧНЫХ  ЗНАНИЙ  УЧАЩИХСЯ  С  ИСПОЛЬЗОВАНИЕМ  НЕЙРОННОЙ  СЕТИ

Садыкова  Рузалина  Разгатовна

аспирант

Башкирского  государственного  педагогического  университета  им.  М.  Акмуллы, 
РФ,  г.  Уфа

E-mail: 

Prediction  of  a  residual  knowledge  of  students  using  neural  NETWORK

Ruzalina  Sadykova

graduate  student,

Bashkir  State  Pedagogical  University  M.  Akmulla, 
Russia,  Ufa

АННОТАЦИЯ

Дана  характеристика  к  прогнозированию  остаточных  знаний  учащихся  при  помощи  нейронных  сетей.  Описан  метод,  позволяющий  использовать  функциональные  возможности  программы  Matlab  для  оценки  остаточных  знаний.

ABSTRACT

The  characteristic  of  a  prediction  residual  knowledge  of  students  with  the  help  of  neural  networks.  The  method,  which  allows  to  use  the  functionality  of  the  program  Matlab  to  evaluate  the  residual  knowledge.

Ключевые  слова:  прогнозирование;  остаточные  знания;  нейронные  сети.

Keywords:  forecasting;  residual  knowledge;  neural  networks.

Одним  из  важных  компонентов,  отражающих  качество  подготовки  учащихся,  является  тестирование  уровня  их  остаточных  знаний.

Остаточные  знания  –  это  знания  учебного  материала,  которые  сохраняются  в  памяти  длительное  время  и  позволяют  ему  использовать  их  в  практической  деятельности  [3,  с.  167].

Забывание  –  один  из  процессов  в  системе  памяти,  проявляющийся  в  невозможности  (неспособности)  припомнить  или  узнать,  либо  в  ошибочном  припоминании  и  узнавании  информации.

Если  задача  будет  решаться  с  помощью  нейронной  сети,  то  необходимо  собрать  данные  для  обучения.  Обучающий  набор  данных  представляет  собой  набор  наблюдений,  для  которых  указаны  значения  входных  и  выходных  переменных. 

Нейронные  сети  –  это  очень  мощный  и  гибкий  механизм  прогнозирования.  Нейронная  сеть  (НС)  –  это  система,  которая  принимает  решения  при  множестве  заданных  условий  (на  входе  много  разных  условий,  по  которым  выдается  решение  на  выходе)  [2,  с.  17].

В  данном  случае  рассмотрим  пример  использования  однослойной  статистической  линейной  нейронной  сети  (функция  newlind)  в  задаче  прогнозирования  остаточных  знаний  учащихся  8а  и  8б  классов,  при  помощи  заранее  полученных  данных.

Проведена  промежуточная  аттестация  учащихся  8а,  8б  классов  по  предмету  «Информатика  и  ИКТ».  Тестовый  материал  (2  варианта)  состоял  из  20  заданий,  каждое  задание  оценивался  в  5  баллов.

Данные  8а  класса  (табл.  1).

Таблица  1.

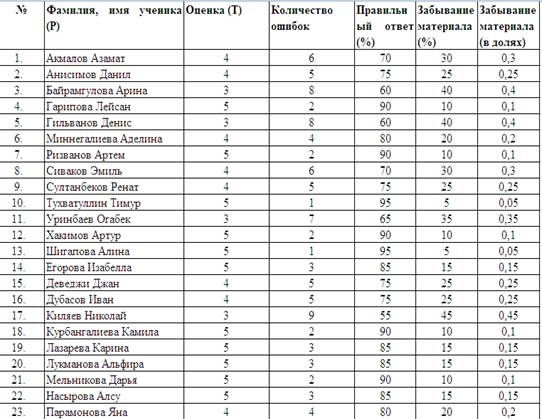
Данные  8б  класса  (табл.  2).

Таблица  2.

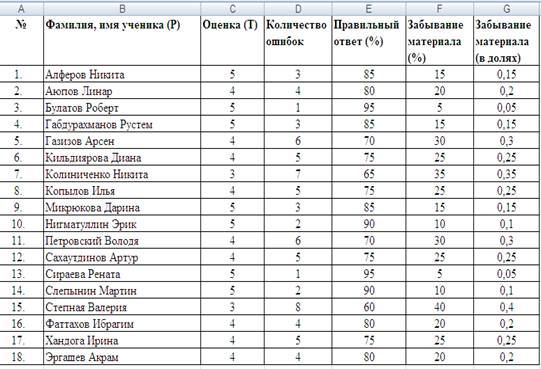
Одношаговое  прогнозирование  –  это  прогнозирование,  когда  один  входной  вектор  отображается  в  выходной  вектор.

Для  моделирования  нейронной  сети  воспользуемся  программой  Matlab/Simulink.  Рассмотрим  функцию  создания  слоя  линейных  нейронов  newlin  (PR,  S,  id,  lr):  PR  –  Rx2  –  матрица  минимальных  и  максимальных  значений  для  R-входных  элементов;  S  –  число  элементов  в  выходном  слое;  id  –  вектор  входной  задержки,  по  умолчанию  [0];  lr  –  коэффициент  обучения,  по  умолчанию  0,01.  Функция  newlin  требует  дополнительного  обучения  [4,  c.  170].

Функция  newlind  (P,T)  проектирования  нового  слоя  методом  наименьших  квадратов  (МНК)  определяет  веса  и  смещения  линейной  сети.  Начальные  веса  и  смещение  по  умолчанию  равны  нулю.  Для  того  чтобы  построить  прогнозы  НС,  необходимо  моделировать  сеть  с  вектором  P,  а  не  с  Т.  Также  вход  (P)  и  выход  (T)  между  собой  связаны  линейно. 

Рассмотрим  алгоритм  настройки  линейной  НС  с  использованием  функции  newlind  на  примере  данных  промежуточной  аттестации  учащихся  8а  и  8б  классов  средней  общеобразовательной  школы.

P  =  [1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  ];

Ряд  забывания:

T  =  [0.300  0.250  0.400  0.100  0.400  0.200  0.100  0.300  0.250  0.050  0.350  0.100  0.050  0.150  0.250  0.250  0.450  0.100  0.150  0.150  0.100  0.150  0.200];

net  =  newlind(P,T);

Веса:  net.IW{1,1};

Смещение:  net.b{1}

y  =  sim(net,P);  plot(P,  T,  P,  y). 

Результат  изображен  на  рис.  1

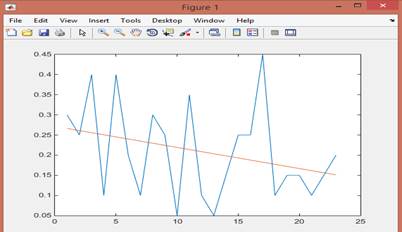
Рисунок  1.

Полученный  результат:

ans  =  -0.0052,  ans  =0.2715

y  =  Columns  1  through  12

  0.2663  0.2611  0.2558  0.2506  0.2454  0.2401  0.2349  0.2296  0.2244  0.2192  0.2139  0.2087

Columns  13  through  23

0.2035  0.1982  0.1930  0.1877  0.1825  0.1773  0.1720  0.1668  0.1616  0.1563  0.1511

На  рис.  1  показано  использование  линейной  НС  newlind  в  задаче  прогнозирования  остаточных  знаний  учащихся  8а  класса,  на  рис.  4  –  8б  класса.  Работа  сети  в  обоих  случаях  может  быть  описана  уравнением  линейной  регрессии.  С  учетом  статистических  критериев,  применяемых  к  уравнению  регрессии  y=0,175  В.

w_range  =  -1:0.1:0.1;  b_range  =  0:0.1:1;

ES  =  errsurf(P,T,w_range,b_range,'purelin');

figure  plotes(w_range,b_range,ES) 

Результат  изображен  на  рис.  2.

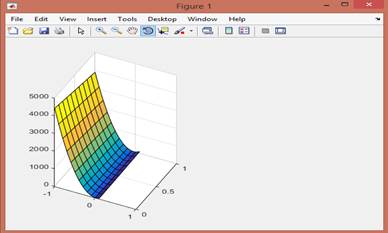
Рисунок  2.

Далее  можем  обучить  сеть  в  два  этапа  с  использованием  функции  группового  обучения  trainb  [1,  c.  47]. 

После  обучения  сеть  способна  предсказать  будущее  значение  заданной  последовательности  на  основе  предыдущих  значений.  Данная  задача  является  основанием  для  дальнейших  исследований.

Список  литературы:

1. Барский  А.Б.  Нейронные  сети:  распознавание,  управление,  принятие  решений.  М.:  Финансы  и  статистика.  2004.  –  170  с. 
2. Галушкин  А.И.  Теория  нейронных  сетей.  Кн.1:  Учебное  пособие  для  вузов.  М.:  ИПРЖ.  –  2000.  –  98  c.
3. Коротков  Э.М.  Качество  образования:  формирование,  факторы  и  оценка,  управление.  М.:  ГГУ.  2002.  –  245  с.
4. Строгонов  А.В.  Использование  нейронной  сети  в  задачах  прогнозирования  деградации  выходных  параметров  ИС  //  Компоненты  и  технологии.  –  2006.  –  №  2.  –  С.  170–175.