РАСЧЕТНЫЕ  НАКЛОННЫЕ  СЕЧЕНИЯ  В  ЖЕЛЕЗОБЕТОННОМ  ЭЛЕМЕНТЕ  ПРИ  ДЕЙСТВИИ  ПОПЕРЕЧНЫХ  УСИЛИЙ

Исаков  Ондасын  Абдрашитович

д-р  техн.  наук,  проф.  архитектуры,  проф.  строительства 
КазНТУ, 
Республика  Казахстан,  г.  Алматы

Кызылбаев  Нурлан  Куттыбаевич

магистр  технич.  наук,  ассистент.проф.,

КазГАСА, 
Республика  Казахстан,  г.  Алматы

Е-mail: 

SETTLEMENT  OBLIQUE  SECTION  IN  REINFORCED  CONCRETE  ELEMENTS  UNDER  THE  EFFECT  OF  LATERAL  FORCES

Ondasyn  Isakov

Ph.D.,  professor  of  architecture,  professor  construction, 
KazNTU, 
Republic  of  Kazakhstan,  Almaty

Nurlan  Kyzylbaev

master  of  Technical  Sciences,  assistant  professor, 
KazGASA, 
Republic  of  Kazakhstan,  Almaty

АННОТАЦИЯ

В  данной  статье  рассматривается  расположение  расчетных  наклонных  сечений  в  железобетонных  элементах  при  поперечных  воздействиях  и  возникающие  в  данных  сечениях  напряженно-деформированные  состояния. 

ABSTRACT

        This  article  describes  the  location  of  the  settlement  inclined  sections  in  the  concrete  elements  in  the  cross-influences  and  emerging  in  these  sections  of  the  stress-strain  state.
 

Ключевые  слова:  деформация;  напряжение;  продольная  арматура;  наклонные  сечения;  продольные  силы;  поперечные  силы;  состояние.

       Keywords:  deformation;  stress;  longitudinal  reinforcement;  inclined  section;  longitudinal  forces;  transverse  force;  condition.

Для  обеспечения  прочности  железобетонного  элемента  по  наклонным  сечениям  в  целом  должна  быть  обеспечена  прочность  любого  наклонного  сечения,  проходящего  в  элементе.  Согласно  общему  правилу,  относящемуся  к  расчету  прочности  элементов  по  нормальным,  наклонным  или  пространственным  сечениям,  в  общем  случае,  рассматривается  последовательный  ряд  сечений  по  длине  элемента,  с  тем,  чтобы  убедиться,  что  все  эти  сечения  удовлетворяют  требованиям  прочности.  В  инженерной  практике  для  отдельных  случаев  с  помощью  специального  анализа  (либо  это  бывает  очевидным)  заранее  устанавливаются  места  расположения  наиболее  опасных  сечений,  для  которых  производится  расчет.  В  представленном  методе  расчета  положение  наклонного  сечения  по  длине  элемента  характеризуется  положением  вершины  наклонной  трещины,  поскольку  в  нормальном  сечении,  проходящем  через  вершину  наклонной  трещины,  учитывается  величина  изгибающего  момента  М  и  влияние  местного  действия  сосредоточенной  нагрузки  Q,  определяющих  характеристики  наклонного  сечения  [1].  Поэтому  в  общем  случае  рассматривается  последовательный  ряд  наклонных  сечений,  характеризуемых  положением  вершины  наклонной  трещины  по  длине  элемента  (рис.1),  для  которых  устанавливаются  величины  изгибающего  момента  М  от  внешней  нагрузки,  характеристики  наклонного  сечения  x,x_o,с,  R_sh,  внутренние  поперечные  усилия  Q_sw,  Q_b1  ,  Q_sз  и  путем  сравнения  их  суммы  с  поперечной  силой  Q  от  внешней  нагрузки,  действующей  в  рассматриваемом  наклонном  сечении,  устанавливается,  удовлетворяет  ли  это  сечение  требованиям  прочности.  Наиболее  опасным  будет  такое  наклонное  сечение,  у  которого  разница  между  внутренними  и  внешними  силами  минимальна.  Такой  подход  может  быть  применен  к  элементам  с  различными  схемами  загружения  и  опирания,  поскольку  она  характеризуется  различным  характером  распределения  изгибающих  моментов  и  поперечных  сил,  а  также  характером  местного  действия  нагрузки,  что  учитывается  в  расчете  при  рассмотрении  последовательного  ряда  сечений.  Это  относится  к  балкам  на  двух  свободных  опорах,  загруженным  сосредоточенными  и  распределенными  нагрузками,  к  консольным  и  неразрезным  балкам  и  т.  д.  В  последнем  случае  следует  учитывать  двузначную  эпюру  изгибающих  моментов  по  длине  элемента,  рассматривая  наклонные  сечения  в  зоне  действия  положительных  и  отрицательных  моментов  с  вершиной  наклонной  трещины  у  соответствующей  сжатой  грани  (рис.  2).  При  этом  наклонное  сечение  не  должно  выходить  за  пределы  зоны  действия  моментов  одного  знака.  Проверка  большого  числа  наклонных  сечений  существенно  увеличивает  трудоемкость  расчета,  поэтому  целесообразно  установить,  хотя  бы  для  наиболее  распространенных  случаев,  положение  наиболее  опасных  наклонных  сечений.  Не  останавливаясь  подробно  на  этой  задаче,  которая  очевидно  может  быть  разрешена  в  дальнейшем  при  разработке  соответствующих  руководств  и  пособий,  также  как  это  делается  сейчас  по  отношению  к  другим  методам  СНиП,  покажем  на  отдельных  примерах,  где  может  быть  принято  расчетное  положение  наиболее  опасного  наклонного  сечения.

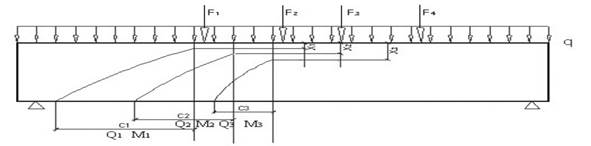
Рисунок  1.  Расположение  расчетных  наклонных  сечений  по  длине  элемента

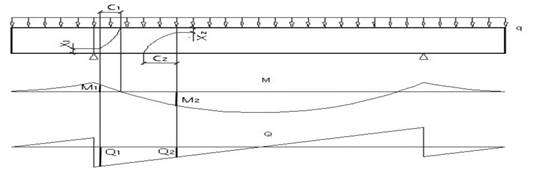
Рисунок  2.  Расположение  расчетных  наклонных  сечений  в  неразрезных  балках

Для  балок  на  двух  свободных  опорах,  загруженных  двумя  сосредоточенными  грузами,  поперечная  сила  Q  между  опорой  и  грузом  остается  постоянной,  а  изгибающий  момент  М  увеличивается  при  приближении  к  грузу.  Поэтому  с  точки  зрения  величины  момента  М  и  поперечной  силы  Q  наиболее  опасным  является  положение  наклонного  сечения  с  вершиной  под  грузом  так,  где  действует  наибольший  изгибающий  момент  (рис.  3).  Однако  на  несущую  способность  по  наклонному  сечению  оказывает  влияние  также  местные  напряжения    вблизи  сосредоточенного  груза,  причем  при  приближении  к  грузу  их  величина  увеличивается,  вызывая  увеличение  сопротивления  R_sh,  значит  и  несущей  способности  сечения.  В  результате  вершина  наиболее  опасной  наклонной  трещины  будет  несколько  отстоять  от  груза.  Проведенный  ранее  анализ  показал,  что  без  большой  погрешности  можно  принять  расчетное  наклонное  сечение  с  вершиной  непосредственно  под  грузом.  При  наличии  нескольких  сосредоточенных  грузов  все  приведенные  выше  рассуждения  остаются  в  силе  и  для  участков  между  грузами.  В  этом  случае  в  качестве  опасных  сечений  следует  рассматривать  наклонные  сечения  с  вершиной  под  каждым  сосредоточенным  грузом  [2].  При  действии  на  элемент  равномерно  распределенной  нагрузки  поперечные  силы  от  опоры  к  середине  пролета  уменьшается,  а  изгибающие  моменты,  наоборот,  возрастают.  Поэтому  положение  вершины  наиболее  опасного  наклонного  сечения  будет  находиться  в  некоторой  промежуточной  точке  между  опорой  и  серединой  пролета  (рис.  4.).

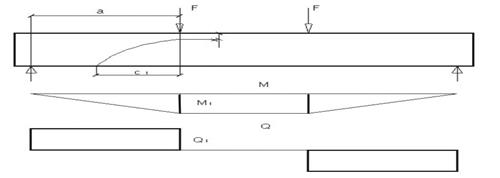
Рисунок  3.  Расположение  расчетного  наклонного  сечения  при  сосредоточенной  нагрузке

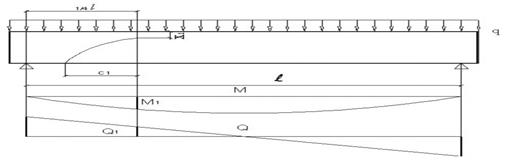
Рисунок  4.  Расположение  расчетного  наклонного  сечения  при  равномерно  распределенной  нагрузке

Для  определения  положения  этой  точки  были  проведены  расчеты  для  балок  с  различной  относительной  длиной  ,  загруженных  равномерно  распределенной  нагрузкой.  Результаты  расчетов  приведены  на  рис.  3.  Как  видно  из  графика,  вершина  опасного  наклонного  сечения  располагается  примерно  на  расстоянии  (0,2—0,3)  l  от  опоры.  Следует  отметить,  что  для  коротких  элементов  эта  точка  смещается  ближе  к  середине  пролета  [3].  Поэтому  можно  было  бы  для  обычных  балок  при  ≥  10  с  достаточной  уверенностью  принять  расчетное  положение  вершины  наиболее  опасного  наклонного  сечения  на  расстояние  ¼  l  от  опоры.  Для  коротких  балок  более  точным  выглядит  решение,  если  принять  это  расстояние  в  виде  некоторой  функции  от  ,  например,  в  виде  0,45-0,02  .  В  неразрезных  и  консольных  балках,  имеющих  двузначную  эпюру  моментов,  помимо  расчетных  наклонных  сечений  в  пролете  следует  также  рассматривать  наклонное  сечение  с  вершиной  над  опорой,  где  действуют  наибольшие  моменты  обратного  знака  (рис.  2.).  Сделанные  выше  выводы  являются  справедливыми  для  элементов  с  постоянными  геометрическими  размерами  и  армированием  по  всей  длине  элемента.  При  изменении  этих  характеристик  следует  рассматривать  наиболее  опасные  наклонные  сечения  в  пределах  каждой  зоны  с  постоянными  геометрическими  размерами  и  армированием  [4].

Окончательные  выводы  о  приемлемости  принятых  положений  наиболее  опасных  наклонных  сечений  будут  сделаны  после  сопоставления  конечных  результатов  расчета  и  опытов.

Список  литературы:

1. Беглов  А.Д.,  Санжаровский  Р.С.  Теория  расчета  конструкций  на  прочность  и  устойчивость.  —  СПб.-М.,  2004.
2. Залесов  А.С.,  Мухамедиев  Т.А.,  Чистяков  Е.А.  Расчет  деформаций  железобетонных  конструкций  по  новым  нормативным  документам.  Бетон  и  железобетон,  №  6,  2002. 
3. Залесов  А.С.  Новый  метод  расчета  прочности  железобетонных  железобетонных  конструкций  М.,  1977. 
4. Кудзис  А.П.,  Двоскина  Л.Г.  Об  оценке  влияния  продольной  арматуры  на  прочность  элементов  в  наклонном  сечении.  —  В  кн.:  Железобетонные  конструкции,  №  8.  Вильнюс,  1977  (ВИСИ).