Статья опубликована в рамках: L Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 30 сентября 2015 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ФИНИТНОЕ УПРАВЛЕНИЕ СЕРВОПРИВОДОМ ПОСТОЯННОГО ТОКА С МИНИМАЛЬНЫМ РАСХОДОМ ЭНЕРГИИ
Капля Егор Викторович
канд. физ.-мат. наук, доцент, ведущий научный сотрудник
филиала Московского энергетического института в г. Волжском,
РФ, г. Волжский
E-mail: ev-kaple@yandex.ru
FINITE CONTROL OF THE DC SERVO WITH A MINIMUM CONSUMPTION OF ENERGY
Egor Kaplya
сandidate of physics and mathematics, associate professor,
leading researcher branch of Moscow power engineering Institute in Volzhsky,
Russia, Volzhsky
АННОТАЦИЯ
Исследована зависимость расхода энергии от длины отрезка терминального управления. Получена формула, позволяющая оценить минимальный расход энергии при терминальном управлении серводвигателем постоянного тока.
ABSTRACT
The dependence of power consumption on the length of the segment terminal control. The formula is derived that allows to estimate the minimum energy consumption when the terminal control servo motor DC.
Ключевые слова: финитное управление; сервопривод; потребляемая энергия.
Keywords: finite control; fixed-time control; servo-driver; servo motor; expenditure energy.
Финитное управление заключается в переводе объекта управления из заданного начального состояния в заданное конечное состояние за ограниченное время [1, с. 54]. Задача поиска оптимальной продолжительности финитного управления (терминального времени) сервоприводом имеет важное практическое приложение в системах управления различными объектами энергетики и, в частности, сервоприводами лопастей ветроэнергетических установок и приводами систем ориентации солнечных батарей. В качестве объекта управления рассмотрим двигатель постоянного тока (ДПТ) с редуктором и механической нагрузкой.
Цель исследования: определение оптимального по минимуму расхода энергии терминального времени управления сервоприводом с ДПТ.
В основе известной [2, с. 148] математической модели сервопривода постоянного тока — система дифференциальных уравнений:
|
|
(1) |
|
|
(2) |
где: ![]() — суммарный момент инерции якоря ДПТ и механизма;
— суммарный момент инерции якоря ДПТ и механизма;
![]() — угол поворота якоря ДПТ;
— угол поворота якоря ДПТ;
![]() — ток в цепи якоря;
— ток в цепи якоря;
![]() — коэффициент пропорциональности, связывающий ток в цепи якоря и развиваемый двигателем вращающий момент
— коэффициент пропорциональности, связывающий ток в цепи якоря и развиваемый двигателем вращающий момент ![]() ;
;
![]() — передаточное число редуктора сервопривода;
— передаточное число редуктора сервопривода;
![]() — управляющее напряжение;
— управляющее напряжение;
![]() — индуктивность цепи якоря;
— индуктивность цепи якоря;
![]() — активное сопротивление цепи якоря;
— активное сопротивление цепи якоря;
![]() — угловая скорость вала двигателя;
— угловая скорость вала двигателя;
![]() — коэффициент противоЭДС, связывающий противоЭДС
— коэффициент противоЭДС, связывающий противоЭДС ![]() с угловой скоростью;
с угловой скоростью; ![]() ;
;
![]() — вращающий момент, создаваемый ДПТ;
— вращающий момент, создаваемый ДПТ;
![]() — момент сопротивления нагрузки, приведенный к валу двигателя. Момент сил сопротивления будем считать линейно зависящим от угловой скорости вращения ротора ДПТ:
— момент сопротивления нагрузки, приведенный к валу двигателя. Момент сил сопротивления будем считать линейно зависящим от угловой скорости вращения ротора ДПТ:
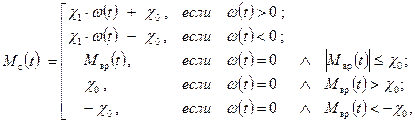
где: ![]() — момент трогания ротора двигателя и механической нагрузки сервопривода, приведенный к валу двигателя;
— момент трогания ротора двигателя и механической нагрузки сервопривода, приведенный к валу двигателя;
![]() — коэффициент сопротивления движению.
— коэффициент сопротивления движению.
При жесткой механической связи вала двигателя и ведомого вала нагрузки посредством зубчатых колес редуктора можно принять: ![]() ;
; ![]() ;
; ![]() , где
, где ![]() ,
, ![]() ,
, ![]() — угол поворота, угловая скорость, угловое ускорение вала нагрузки, соответственно;
— угол поворота, угловая скорость, угловое ускорение вала нагрузки, соответственно; ![]() — угловое ускорение якоря ДПТ (рис. 1).
— угловое ускорение якоря ДПТ (рис. 1).

Рисунок 1. Электродвигатель с редуктором
Структурная схема автоматизированной системы управления сервоприводом с блоком финитного управления (БФУ) представлена на рис. 2. На вход БФУ подаются заданные конечные значения фазовых координат вала нагрузки: ![]() ,
, ![]() ,
, ![]() .
.
Схема, показанная на рис. 2, предполагает использование датчика углового положения (энкодера). Угловая скорость и угловое ускорение вычисляются путём дифференцирования углового перемещения механической нагрузки. Текущие значения фазовых координат сравниваются с заданными. БФУ вычисляет и формирует управляющий сигнал ![]() на основе выбранного закона терминального управления.
на основе выбранного закона терминального управления.
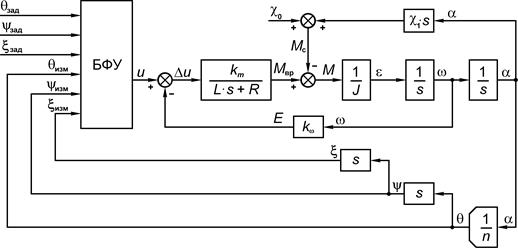
Рисунок 2. Структурная схема САУ сервоприводом с БФУ
Известный [1, с. 69] закон финитного управления применительно к сервоприводу на основе ДПТ представим в следующем виде:
|
|
(3) |
где: ![]() — коэффициент пропорциональности между напряжением на обмотке ДПТ и угловым ускорением ротора;
— коэффициент пропорциональности между напряжением на обмотке ДПТ и угловым ускорением ротора; ![]() ;
;
![]() — момент времени окончания переходного процесса;
— момент времени окончания переходного процесса;
![]() — момент времени начала процесса управления;
— момент времени начала процесса управления;
![]() — терминальное время;
— терминальное время;
![]() — жёсткость управления.
— жёсткость управления.
Рассмотрим модель процесса управления сервоприводом, обладающим следующими характеристиками: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() при следующих начальных и конечных условиях:
при следующих начальных и конечных условиях: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Примем:
. Примем: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Энергия, потребляемая якорем ДПТ от источника электрической энергии в процессе финитного управления сервоприводом, выражается интегралом:
|
|
(4) |
Ток в цепи якоря ДПТ представим решением уравнения (2) относительно ![]() :
:
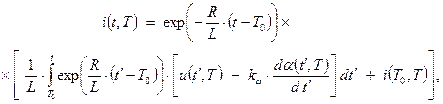
где ![]() — ток в цепи якоря в момент времени
— ток в цепи якоря в момент времени ![]() . При пуске двигателя можно принять
. При пуске двигателя можно принять ![]() , т. к. ток через индуктивный элемент не может измениться мгновенно.
, т. к. ток через индуктивный элемент не может измениться мгновенно.
Оптимальное терминальное время ![]() соответствует минимуму функции
соответствует минимуму функции ![]() . Зависимость
. Зависимость ![]() при заданных начальных и конечных условиях и заданных характеристиках сервопривода имеет единственный минимум (рис. 3).
при заданных начальных и конечных условиях и заданных характеристиках сервопривода имеет единственный минимум (рис. 3).
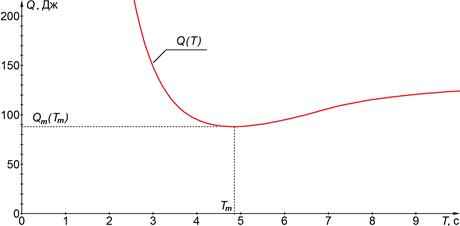
Рисунок 3. График зависимости ![]()
В результате минимизации функции (4) при использовании сигнала (3) получена [3, с. 30] новая формула:
|
|
(5) |
Формула (5) позволяет оценить оптимальное терминальное время при повороте механической нагрузки из одного неподвижного состояния в другое.
Список литературы:
- Батенко А.П. Управление конечным состоянием движущихся объектов. — М.: Советское радио, 1977. — 256 с.
- Фираго Б.И., Павлячик Л.Б. Теория электропривода. — Мн.: ЗАО “Техноперспектива”, 2004. — 527 с.
- Капля Е.В. Энергоэффективное терминальное управление серводвигателем постоянного тока. // Автоматизация процессов управления. — 2015. — № 1. — С. 27—33.
дипломов


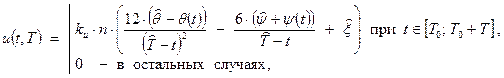
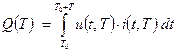 .
.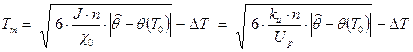 .
.
Оставить комментарий