МОДЕЛИРОВАНИЕ МЕТОДОМ МОНТЕ-КАРЛО ПЕРЕНОСА ЭЛЕКТРОНОВ В АРСЕНИДЕ ГАЛЛИЯ В СИЛЬНЫХ ЭЛЕКТРИЧЕСКИХ ПОЛЯХ

Стамбакио Егор Сергеевич

аспирант, кафедра физической электроники и нанотехнологий, Белорусский Государственный Университет, г. Минск, Республика Беларусь

E-mail:

MONTE-CARLO SIMULATION OF ELECTRON TRANSPORT IN GAAS IN HIGH ELECTRIC FIELDS

Egor Stambakio

P.G., Department of Physical Electronics and Nanotechnology, Belarusian State University, Minsk, Belarus

АННОТАЦИЯ

Целью данной работы была разработка физико-математической модели, а также реализующих ее алгоритма и программы для расчета многочастичным методом Монте-Карло кинетических параметров, характеризующих перенос электронов в GaAs в сильных электрических полях. Для расчета интенсивности рассеяния электронов на ионах примеси в алгоритм включена модель исключения третьего тела, или модель Ридли. Разработанная программа позволяет моделировать зависимость дрейфовой скорости электронов от напряженности приложенного электрического поля при различных концентрациях легирующей примеси, а также другие кинетические параметры (среднюю энергию носителей заряда, подвижность и др.), характеризующие перенос электронов в GaAs в сильных электрических полях.

ABSTRACT

The purpose of this work is the development of a simulation model, an algorithm and the corresponding computer program for the simulation of kinetic parameters which describe electron transport in GaAs in high electric fields. The Readley model is used to calculate electron scattering frequency on impurities. The designed program allows simulating relations between electron drift speed and electric field intensity according to different concentration of impurity, and other kinetic parameters (mobility and average energy of charge carriers, etc.) which describe electron transport in GaAs in high electric fields.

Ключевые слова: монте-карло; GaAs; перенос электронов; моделирование.

Keywords: monte-carlo; GaAs; electron transport; simulation.

Введение

Численное моделирование является одним из важнейших этапов создания полупроводниковых интегральных схем с субмикронными и нанометровыми размерами активных элементов. Компьютерные модели электрофизических свойств полупроводниковых материалов и приборных структур дают возможность рассчитывать различные характеристики интегральных приборов при изменении технологии их изготовления и структуры. При построении таких моделей необходимо учитывать влияние на процессы переноса носителей заряда в полупроводниковых материалах специфических эффектов, обусловленных сильными электрическими полями и структурой кристаллической решетки полупроводника. При этом последовательное уменьшение размеров элементов интегральных схем требует постоянной разработки новых и совершенствования известных физико-математических моделей, алгоритмов и программ численного моделирования приборов и структур. Одним из наиболее перспективных методов такого моделирования является метод Монте-Карло [1, 2, 4, 5].

Целью данной работы была разработка физико-математической модели, а также реализующих ее алгоритма и программы для расчета многочастичным методом Монте-Карло кинетических параметров, характеризующих перенос электронов в GaAs в сильных электрических полях.

Модель переноса

Физико-математические модели переноса носителей заряда в полупроводниках на основе метода Монте-Карло строятся на представлении свободного дрейфа этих носителей, прерываемого актами рассеяния на некоторых центрах рассеяния. Эти центры рассеяния представляют собой дефекты кристаллической решетки материала полупроводника, полярные оптические и акустические фононы, примесные центры (нейтральные точечные дефекты и ионы), другие электроны (электрон-электронное рассеяние). Учет всех механизмов рассеяния при моделировании процессов переноса заряда является сложной задачей, поскольку вероятность каждого механизма рассеяния зависит от результата предыдущего рассеяния, длины пробега, приложенного поля, температуры. После каждого акта рассеяния для определения направления движения носителя и его начальной энергии необходимо рассчитывать волновой вектор носителя после рассеяния, а также полярный и азимутальный углы рассеяния. Во время пробега между актами рассеяния носители движутся согласно направлению поля и знака заряда носителя и изменяют свою энергию. В момент рассеяния направление движения носителя отклоняется на некоторый угол (вплоть до разворота в обратном направлении). Различают упругие и неупругие механизмы рассеяния. При упругом рассеянии энергия носителя остается равной энергии непосредственно перед рассеянием, а при неупругом рассеянии часть энергии носителя поглощается центром рассеяния либо испускается в виде фонона.

Алгоритм метода Монте-Карло

Метод Монте-Карло - это численный статистический метод, позволяющий численно решать громоздкие уравнения, характеризующие перенос носителей заряда. В общем случае при моделировании переноса носителей заряда вероятностным образом определяется начальное состояние носителей, после чего пошагово прослеживается их дрейф в материале полупроводника. Механизм для каждого акта рассеяния определяется также статистически, исходя из вклада каждого механизма в общую вероятность рассеяния.

Если, например, в модели учитывается N механизмов рассеяния, то для каждого механизма рассчитывается частота рассеяния (вероятность рассеяния в единицу времени). Далее все частоты последовательно суммируются, и выбирается некоторое значение частоты рассеяния Г, которое больше либо равно максимальному суммарному значению частот во всем диапазоне изменения энергии носителей. Этот прием значительно упрощает расчеты. Далее случайным образом на отрезке 0÷Г выбирается механизм для данного акта рассеяния, согласно законов которого определяются волновой вектор носителя после рассеяния и соответствующие углы. Если случайное значение попадает в верхний интервал от W_N до Г, то движение частицы продолжается без изменения параметров (имеет место так называемое саморассеяние).

На рис. 1 приведена диаграмма, поясняющая процедуру выбора механизма рассеяния для конкретного значения энергии электрона Е. Здесь – интенсивность рассеяния для i-го механизма; r – случайное число на отрезке ; j – номер выбранного механизма рассеяния. Согласно рис. 1, если для какой-либо энергии носителя выполняется неравенство , то выбирается механизм рассеяния с номером j.

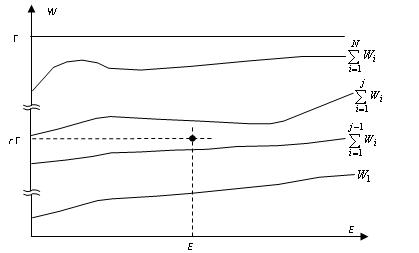
Рис. 1. Диаграмма, поясняющая процедуру выбора механизма рассеяния для конкретного значения энергии электрона Е.

Для моделирования стационарных процессов применяется одночастичный метод Монте-Карло, когда моделируется пробег одной частицы множество раз, а результат находится как среднее значение по всем пробегам. При моделировании нестационарных процессов (переменное внешнее воздействие) используется многочастичный метод Монте-Карло. В отличие от одночастичного, в многочастичном методе моделируется перенос некоторого, достаточно большого числа носителей (не менее 1000 электронов) при фиксированном значении определенного динамического параметра, а усреднение ведется по этому ансамблю. Далее прослеживается новый пакет носителей при изменившемся значении данного параметра. Таким образом, многочастичный метод является более ресурсоемким и сложным в реализации, чем одночастичный метод.

На рисунке 2 приведены временные диаграммы движения электрона и алгоритма моделирования этого движения многочастичным методом Монте-Карло [2]. Инкремент временного параметра τ вычисляется как величина, обратная Г. Таким образом это время свободного пробега носителя.

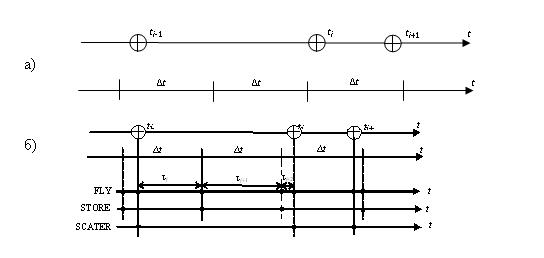
Рис. 2. Временная диаграмма поведения электрона (а) и временная диаграмма алгоритма моделирования (б) [2].

Расчет интенсивностей рассеяния

Поскольку целью данной работы было моделирование методом Монте-Карло переноса электронов в арсениде галлия в сильных электрических полях, в вычислительной модели были учтены следующие виды рассеяния: рассеяние на акустических и полярных оптических фононах, междолинное Г-L внутридолинное рассеяние, рассеяние на ионах примеси и ударная ионизация. Формулы для расчета частот рассеяния в арсениде галлия взяты из [2, 3]. При этом одной из основных задач в данной работе было определение влияния концентрации легирующей примеси на величину дрейфовой скорости электронов.

Поскольку известные модели для расчета частоты рассеяния на ионах примеси (модель Конуэлл-Вайскопфа и Брукса-Херринга) применимы лишь для определенных, достаточно узких диапазонов концентрации примесей, в данной работе применен алгоритм, перекрывающий области применения этих моделей. Данный алгоритм основан на включении в него модели исключения третьего тела, или модели Ридли [3].

Если предположить, что вероятность p существования другого центра рассеяния, по отношению к которому прицельный параметр b будет находиться в интервале , равна , то есть вероятность отсутствия рассеивающих центров с прицельным параметром, меньшим b можно представить в виде , где  – среднее расстояние между ионами.

Таким образом, вероятность  можно считать множителем, исключающим влияние третьего тела или множителем экранирования третьим телом. Этот множитель должен входить в вероятности всех процессов двухчастичного рассеяния, в которых центр рассеяния локализованы. Он должен учитываться в принципе во всех процессах рассеяния на примеси, как нейтральной, так и заряженной.

Для модели исключения третьего тела оказывается несложным получить выражение для расчета вероятности рассеяния в единицу времени с учетом весового множителя [1]:

,

где  – частота рассеяния, рассчитанная по модели Брукса-Херринга.

Для расчета полярного угла рассеяния в [6] была предложена следующая формула

где

,

,

,

а максимальное значение прицельного параметра определяется из неравенства

.

Результаты вычислительного эксперимента

Разработанные в данной работе алгоритм и реализующая его программа для расчета кинетических параметров переноса электронов в арсениде галлия методом Монте-Карло продемонстрировали адекватность полученных нами результатов с экспериментальными результатами и результатами компьютерного расчета других авторов (рис. 3). На рис. 3 приведена рассчитанная нами зависимость дрейфовой скорости электронов в GaAs от величины напряженности электрического поля Е при температуре Т=300К, а на рис. 4, 5, 6 в качестве примера представлены зависимости  при различных температурах (рис. 4) и концентрации легирующей примеси.

Рис. 3. Рассчитанная зависимость дрейфовой скорости электронов в GaAs при температуре 300К и концентрации примесных ионов 10_­­^21­ м^-3. Для сравнения результаты моделирования других авторов [4, 5] показаны крестиками, а экспериментальные данные [5] – квадратами.

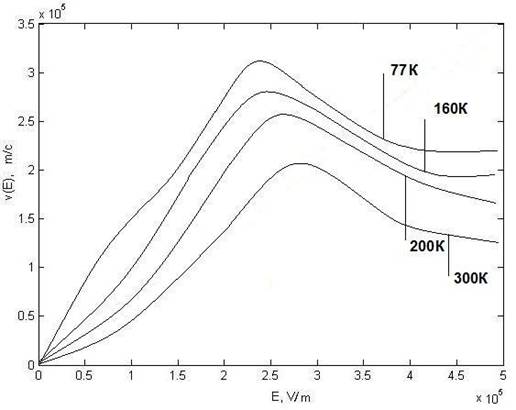
Рис. 4. Рассчитанные зависимости дрейфовой скорости электронов от напряженности электрического поля при температурах 77÷300К. Концентрация ионов примеси 10_­­^21­ м^-3.

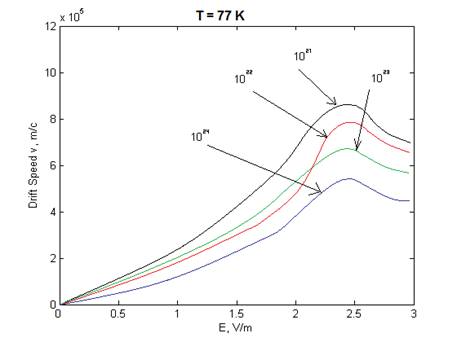
Рис. 5. Полученная зависимость дрейфовой скорости электронов от напряженности электрического поля в GaAs при температуре 77 K и различных концентрациях примеси. Стрелками обозначены соответствующие кривые для различных концентраций, в м^-3.

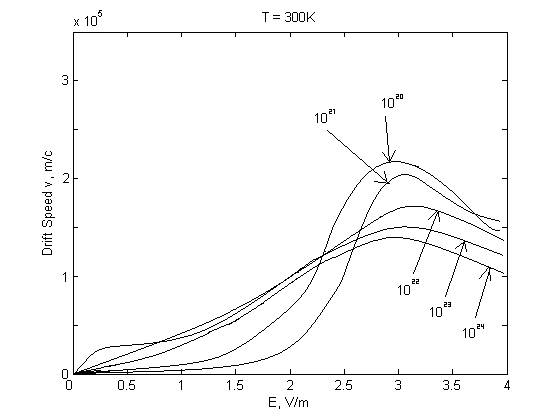
Рис. 6. Полученная зависимость дрейфовой скорости электронов от напряженности электрического поля в GaAs при температуре 300K и различных концентрациях примеси. Стрелками обозначены соответствующие кривые для различных концентраций, в м^-3.

Выводы

Анализ полученных в представленной работе результатов позволил сделать следующие основные выводы:

При температуре 300 К переходы из Г в L долины GaAs наблюдаются при напряженности электрического поля ~ 2,5 кВ/см, что хорошо согласуется с известными экспериментальными данными для GaAs:

С уменьшением температуры дрейфовая скорость электронов возрастает, а переход из Г в L долины наблюдается при меньшем электрическом поле, что связано с уменьшением интенсивности рассеяния электронов на фононах.

При возрастании концентрации ионизированной примеси в GaAs дрейфовая скорость электронов спадает, что связано с возрастанием количества рассеивающих центров на пути пробега электрона. При этом участок характеристики с отрицательной дифференциальной проводимостью сглаживается, что дает возможность управлять данной величиной, меняя степень легирования GaAs.

В заключение отметим, что разработанная программа позволяет моделировать помимо дрейфовой скорости и другие кинетические параметры (среднюю энергию носителей заряда, подвижность и др.), характеризующие перенос электронов в GaAs в сильных электрических полях.

Список литературы:

1 Борздов В. М., Жевняк О. Г., Комаров Ф. Ф., Галенчик В. О. Моделирование методом Монте-Карло приборных структур интегральной электроники. Минск: БГУ 2007.

2 Иващенко В. М., Митин В. В. Моделирование кинетических явлений в полупроводниках. Метод Монте-Карло. – Киев: Навукова думка, 1990.

3 Ридли Б. К. Квантовые процессы в полупроводниках. М.: Мир, 1986. – 304 с.

4 Хокни Р., Иствуд Дж. Численное моделирование методом частиц. – М.: «Мир», 1987.

5 Шур М. Физика полупроводниковых приборов. М.: Мир, 1992.

6 Speransky D. S. Monte Carlo simulation of ionized impurity scattering process in bulk silicon, NDTCS’08.