ПРОТИВОРЕЧИЕ В ОСЕСИММЕТРИЧНО КЛАССИЧЕСКОЙ ЗАДАЧЕ ЛАМЕ О НАПРЯЖЕННОМ СОСТОЯНИИ УПРУГОГО ЦИЛИНДРА

Абдеев Борис Масгутович

канд. техн. наук, профессор ВКГТУ, г. Усть-Каменогорск

Муслиманова Гульнар

канд. техн. наук, доцент ВКГТУ, г. Усть-Каменогорск

E-mail:

CONTRADICTION IN AXISYMMETRIC CLASSICAL PROBLEM ABOUT STRESS Lame STATE OF THE ELASTIC CYLINDER

Boris Аbdeev

Candidate. Technical., professor of EKSTU, Ust-Kamenogorsk

Gulnar Muslimanova

Candidate. Technical. Science, dotsent of EKSTU, Ust-Kamenogorsk

АННОТАЦИЯ

Процедурой предельного перехода, когда внутренний радиус цилиндра стремиться к нулю, доказано, что известная классическая осесимметричная модель Ламе, аппроксимирующая в условиях плоской деформации напряженное состояние однородного изотропного цилиндрического тела, не является корректной и адекватной с физико-математической точки зрения, поскольку она: 1) не отражает фактический характер распределения напряжений в материале при коэффициенте Пуассона меньше 0,5; 2) противоречит теореме единственности решения задачи линейной теории упругости; 3) не согласуется с принципом локальности эффекта самоуравновешенной нагрузки (принципом Сен-Венана).

ABSTRACT

The procedure of passage to the limit when inner radius of a cylinder component tends to zero has proved that known classical axisymmetric Lame model which approximates in conditions of plane deformation of homogeneous isotope cylindrical body stressed state is not correct and adequate in terms of physics and mathematics. There are some reasons of it: 1) it doesn’t reflect a real stress pattern in a matter with Poisson's constant less 0.5; 2) it contradicts the theorem of uniqueness solution of linear elasticity problem; 3) it doesn’t correspond with the principle of locality of self-balanced load effect (Saint Venants' principle)

Ключевые слова: осесимметричность; деформация; упругость.

Keywords: axisymmetric; strain; elasticity

Для толстостенной цилиндрической оболочки из однородного, изотропного и линейно-упругого материала радиальное , кольцевое   и осевое  нормальные напряжения при плоской деформации   аппроксимируются зависимостями    [3]  (рисунок 1а), в которых , - соответственно, внутреннее и наружное равномерно распределенные давления, действующие на поверхностях трубы, имеющих радиусы r=a и r=b, а μ - коэффициент Пуассона.

В механике твердого деформируемого тела данная модель известна как фундаментальное решение французского математика и инженера Габриэля Ламе [3, 4]. Его частным случаем для сплошного цилиндра, не имеющего отверстия, когда a=0 и = [3, 4], является постоянство внутренних силовых характеристик [1]:

                                                     (1)

                                                          (2)

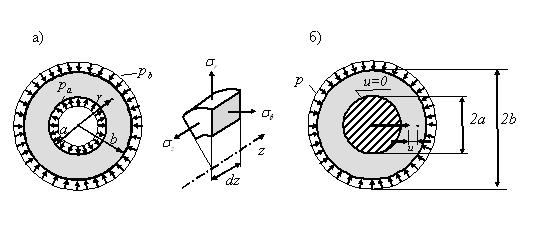
Рисунок 1. Расчетные схемы к решению задачи Ламе [3, 4]:

а) в напряжениях , , ;

б) через функцию перемещений u(r)

Авторами этой работы доказано, что формулы (1)—(2) не являются корректными с физико-математической точки зрения, поскольку они противоречат некоторым основополагающим аспектам механики твердых сплошных сред, касающимся фактического характера распределения напряжений в материале осесимметрично-деформируемого цилиндрического тела.

Для обоснования данного утверждения рассмотрим иной вариант решения задачи Ламе, когда а=0, в основу которого положим расчетную сxему с абсолютно жесткой границей r=a, принимая допущение, что внутренняя часть цилиндра является недеформируемой (рисунок 1б).

С точностью до произвольных постоянных  функция радиального перемещения u=u(r) носит гиперболический характер (рисунок 1б) [1] :

,  .                                         (3)

Напряжения ,  связаны с переменной u(r) функциональной зависимостью обобщенного закона Гука, учитывая соотношение (3) [1,3]:

;                        (4)

где верхний знак относится к , а E - модуль упругости материала.

В соответствии с моделью, изображенной на рисунке 1б, находим константы  из кинематического и статического краевых условий:

, ,                                                       (5)

раскрывая которые, с помощью выражений (3)-(4), будем иметь, после подстановки  в (4):

;                                (6)

.                           (7)

Полагая r=a в формуле (6), определяем параметры ,  и для граничных точек, расположенных на внутренней поверхности оболочки, учитывая (7) (рисунок 1б):

.             (8)

Переходя в соотношениях (8) к пределу при 0, получаем искомое второе решение, описывающее напряженное состояние в центре поперечного сечения цилиндра:

.                                           (9)

Выведенные зависимости (9) для ,  не совпадают с фундаментально-классическим решением (1)—(2), вытекающим из общих формул Ламе [3, 4]. Этот парадоксальный результат противоречит теореме единственности для любого упругого тела, находящегося в естественном состоянии [3].

Тождественность обоих решений (1)—(2) и (9) будет только в том случае, когда коэффициент Пуассона μ=0,5, то есть при допущении о несжимаемости материала [1].

Следует отметить, что и полученные новые формулы (9) не являются правильными, поскольку радиальное напряжение (0)=-2p(1-μ)>(b)=-p при , что не согласуется с принципом локальности эффекта самоуравновешенной нагрузки p (или принципом Сен-Венана [3]), согласно которому в осесимметричном сплошном цилиндре из твердого материала все напряжения должны уменьшаться от внешней границы r=b к центру r=0. При этом очевидно, что неравномерность напряженного состояния будет возрастать с увеличением диаметра 2b цилиндрического тела и эта особенность, моделируемого физико-механического процесса, проиллюстрирована на рисунке 2, где показан примерный (гипотетический) вид соответствующих эпюр  и .

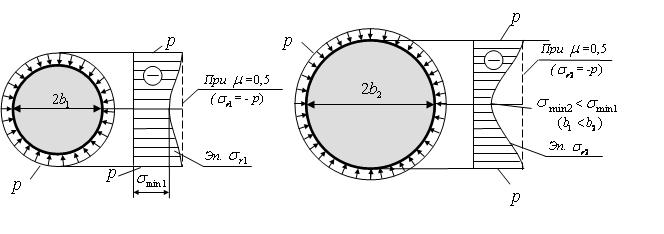
Рисунок 2. Гипотетические эпюры радиальных напряжений

в зависимости от диаметра цилиндра

Выявленный парадокс указывает на неадекватность механико-математической модели Ламе, использованной в решении данной задачи теории упругости. Как уже отмечено, формулы (1)—(2) и (9) дают идентичный и точный ответ:

,                                         (10)

если коэффициент μ=0,5, то есть когда объём тела при деформации не изменяется, что возможно и реально подтверждается только для жидких веществ (без учета их собственной массы), находящихся в резервуарах под избыточным давлением p, а также (приближенно) для различных резин, у которых значения μ близки к 0,5(μ=0,480,496) [2].

Аналогичные противоречия, устранимые при μ=0,5 с тем же результатом (10), имеют и общие исходные функциональные соотношения (6)—(7) к расчетной схеме рисунка 1б, когда  a  Например, при μ=0,3 (стaль), a=0,5b напряжение (a)=-1,273p>(b)=-p и объяснить этот неправильный результат с общепринятой точки зрения невозможно, не предположив наличия какого-то скрытого дефекта в расчетно-теоретической модели Ламе.

Рассмотренный проблемно-инновационный вопрос фундаментально-прикладной механики является актуальным для многих отраслей техники, в том числе машиностроения при оценке несущей способности прессовых соединений в виде монтируемых с натягом сопрягаемых составных деталей цилиндрической формы [1] .

Список литературы:

1.Биргер И. А., Мавлютов Р. Р. Сопротивление материалов: Учебное пособие. — М.: Наука,1986.—560 с.

2.Лавендел Э. Э. Расчет резинотехнических изделий. — М.: Машиностроение, 1976.—232с.

3.Тимошенко С. П., Гудъер Дж. Теория упругости. /Перевод с англ. М. И. Рейтмана под ред. Г. С. Шапиро. — М.: Наука, 1975.—576 с.

4.Lame G. Lecons sur la theorie matematique de l^’ elasticite des corps solides. Paris, Bachelier, 1852, 335 p.