ОПТИМАЛЬНОЕ  ПО  БЫСТРОДЕЙСТВИЮ  УПРАВЛЕНИЕ  ДВУМЕРНОЙ  МОДЕЛЬЮ  ПРОЦЕССА  ПЕРИОДИЧЕСКОГО  ИНДУКЦИОННОГО  НАГРЕВА

Шарапова  Ольга  Юрьевна

аспирант,  СамГТУ,  г.  Самара

E-mail:  o_sharapova@mail.ru

Индукционные  нагревательные  установки  (ИНУ)  периодического  действия  широко  применяются  на  практике  для  индукционного  нагрева  металлов  перед  последующей  обработкой  давлением,  поскольку  они  обладают  рядом  технико-экономических  преимуществ  по  сравнению  с  конкурентоспособными  технологиями.

В  статье  представлены  результаты  моделирования  и  оптимизации  температурных  полей  по  объему  заготовки  в  ходе  индукционного  нагрева  с  использованием  численной  двумерной  электромагнитно-тепловой  модели  процесса.  Сформулирована  и  решена  задача  оптимального  управления  (ЗОУ)  ИНУ  периодического  действия  по  критерию  быстродействия.

Численная  двумерная  модель  процесса  индукционного  нагрева  металла  (ПИНМ)

Для  численного  моделирования  ПИНМ  был  использован  конечно-элементный  специализированный  программный  продуктов  Cedrat  FLUX,  предназначенный  для  многопараметрического  электромагнитного,  теплового  анализа,  для  построения  сетки  детали  и  витков  индуктора  использовались  треугольные  элементы  и  четырёхугольные  в  области  скин-эффекта,  а  для  сетки  окружающего  пространства  -  треугольные  элементы  [2,  с.  180].  Алгоритм  решения  задачи  моделирования  представляет  собой  последовательную  итерационную  процедуру,  включающую  гармонический  электромагнитный  анализ  и  переходный  тепловой  анализ.

Постановка  и  решение  задачи  оптимального  по  быстродействию  управления  двумерной  численной  моделью  ПИНМ. 

Процесс  периодического  индукционного  нагрева  однозначно  определяется  пространственно-временным  распределением  температуры  нагреваемого  тела  ,  где    это  время,  а    пространственные  координаты,  учитывающие  неравномерное  распределение  температуры  как  по  радиусу  (),  так  и  вдоль  оси  цилиндрического  слитка  конечной  длины  ().  При  этом  температурное  поле  заготовки,  моделируется  с  помощью  описанной  выше  двумерной  нелинейной  численной  модели  [2,  с.  180],

В  качестве  управляющего  воздействия  рассматривается  напряжение  источника  питания  .  Ограничение  на  управляющее  воздействие    вводится,  исходя  из  некоторой  заранее  известной  максимальной  величины  ,  определяемой  энергетическими  возможностями  ИНУ,  и  имеет  вид:

                                                 (1)

В  качестве  критерия  оптимальности  для  обеспечения  максимальной  производительности  установки  рассматривается  минимальное  время  нагрева  .

Применительно  к  исследуемому  в  данной  статье  классу  задач  оптимизации  индукционная  установка  в  конечный  момент  времени    должна  обеспечивать  нагрев  металлической  заготовки  до  заданной  температуры    с  допустимым  температурным  отклонением  по  сечению  заготовки  :

                                      (2)

Задача  оптимального  по  быстродействию  управления  ИНУ  может  быть  сформулирована  следующим  образом: 

Необходимо  найти  такое  переменное  во  времени  управляющее  воздействие  ,  стеснённое  ограничением  (1),  которое  обеспечивает  перевод  нагреваемого  изделия  с  начальным  распределением  температуры    в  заданное  целевое  множество  (2),  за  минимально  возможное  время  .

Для  общей  нелинейной  задачи  оптимального  по  быстродействию  управления  процессами  нестационарной  теплопроводности  с  внутренним  тепловыделением  [1,  с.  149],  стандартные  процедуры  принципа  максимума  определяют  –параметризованное  представление  управляющего  воздействия    в  форме  кусочно-постоянной  функции  времени:

                             (3)

однозначно  задаваемой  с  точностью  до  числа  N  и  длительностей    интервалов  своего  постоянства,  выступающих  в  роли  искомых  параметров  и  зависящих  только  от  требуемой  точности  нагрева    в  (2),  где  N  может  быть  найдено  по  заданной  величине    по  общей  методологии  альтернансного  метода  [1,  149].  В  итоге  осуществляется  процедура  редукции  исходной  задачи  к  задаче  полубесконечной  оптимизации:

           (4)

где  зависимости    находятся  по  численной  FLUX  -  модели  объекта  при  управлении  вида  (3).

Ниже  приводятся  примеры  решения  ЗОУ  по  критерию  быстродействия  процесса  индукционного  нагрева  стальных  цилиндрических  заготовок.  Некоторые  исходные  данные  по  конструктивным  характеристикам  нагревателя  и  параметрам  заготовки:  радиус  заготовок  52,5  мм,  длина  900,  начальная  20  ºC  и  заданная  1250  ºC  температура  заготовки,  длина  индуктора  1,046  м,  частота  питающего  тока  2300  Гц,  напряжение  источника  питания  470  В. 

Рассмотрим  случай,  когда  заданная  точность  нагрева  совпадает  с  предельно  достижимой  точностью    при  одноинтервальном  управлении.  Согласно  альтернансным  свойствам  форме  кривых  результирующего  распределения  температур  соответствует  следующая  система  уравнений: 

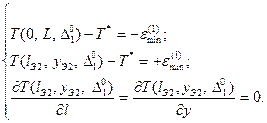                              (5)

решаемая  относительно  искомой  длительности    интервала  нагрева,  минимакса    и  координат  точки  экстремума  .

На  рис.  1  представлен  результат  расчета  температурного  распределения  по  объему  стальной  цилиндрической  заготовки  в  конце  оптимального  по  быстродействию  процесса  нагрева.  Длительность  процесса  нагрева  составляет  541,6  с.,  минимальное  температурное  отклонение  на  выходе  .  Полученная  точность  нагрева  не  соответствует  технологическим  требованиям,  предъявляемым  к  данному  процессу.  Поэтому  необходимо  применение  двухинтервального  алгоритма  оптимального  управления.

Данному  случаю  соответствует  двухпараметрическое  представление  управляющего  воздействия  при  N=2  в  (3).  В  качестве  оптимизируемых  параметров  выступают  длительности  интервалов  нагрева  и  выравнивания  температур,  а  максимальное  абсолютное  отклонение  распределения  температуры  по  объему  заготовки  от  заданного  значения  представляет  собой  минимакс  .  Результирующая  система  уравнений  имеет  вид:

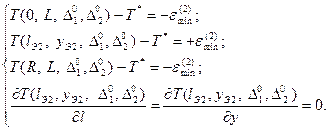                        (6)

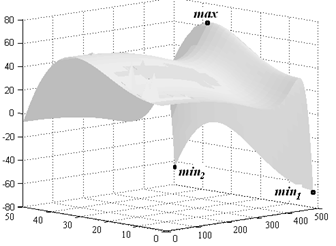
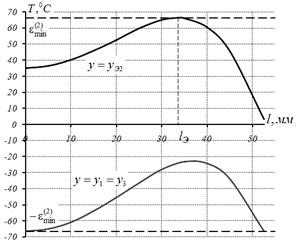
Рисунок  2.  Результирующее  распределение  температур  при  двухинтервальном  управлении:  а  –  по  объему  заготовки;  б  –  в  сечениях  с  максимальными  температурными  отклонениями

На  рис.  2  представлено  температурное  распределение  по  соответствующим  сечениям  заготовки  в  конце  оптимального  процесса  управления.  Длительность  интервала  нагрева  составляет  563,85  с.,  интервала  выравнивания  температур  –  13,3  с.,  . 

Пусть  далее  заданное  значение    удовлетворяет  неравенству  .  В  результате  для  решения  задачи  быстродействия  имеем  систему  четырех  уравнений:

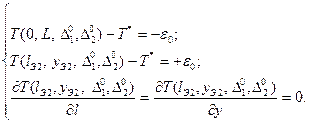                       (7)

При  заданном  значении    эту  систему  следует  решать  относительно  четырех  неизвестных  –  длительностей,    двухинтервального  управления  и  координат  внутренней  точки  максимума  .

В  данном  случае  максимальное  отклонение  в  конце  оптимального  процесса  соответствует  .  Длительность  интервала  нагрева  с  максимальным  напряжением  составляет  556  с.,  продолжительность  интервала  выравнивания  температур  –  6,6  с.

Анализ  результатов,  полученных  при  решении  задачи  оптимального  по  быстродействию  управления  процессом  индукционного  нагрева  заготовки,  показывает,  что  применение  альтернансного  метода  приводит  к  повышению  точности  нагрева  в  классе  управляющих  воздействий  с  фиксированным  числом  интервалов  постоянства,  обеспечивает  сокращение  времени  процесса  и  позволяет  найти  технически  реализуемые  решения  задачи  быстродействия  для  обусловленных  технологическими  требованиями  величин    для  которых  она  становится  неразрешимой  стандартными  способами

Список  литературы

1.Рапопорт  Э.Я.  Оптимизация  процессов  индукционного  нагрева  металла.  –  М.:  Металлургия,  1993.  –  279  с.

2.Шарапова  О.Ю.  Численное  моделирование  процесса  периодического  индукционного  нагрева  на  базе  конечно-элементного  программного  пакета  FLUX  //  Вестник  Самар.  гос.  техн.  ун-та.  Сер.  Технические  науки.  –  2011.  –  №7  (28).  –  C.  180  –  185.