ВЛИЯНИЕ СОСТОЯНИЯ ЭЛЕМЕНТОВ МУЛЬТИСЕРВИСНОЙ СЕТИ СВЯЗИ НА ОЦЕНКУ ПОКАЗАТЕЛЕЙ ЭКСПЛУАТАЦИОННОЙ НАДЁЖНОСТИ И ОТКАЗОУСТОЙЧИВОСТИ

Дроздов Игорь Александрович

канд. техн. наук, доцент, Академия ФСО России, РФ, г. Орёл

E-mail: 19digor63@mail.ru

Константинов Сергей Владимирович

преподаватель, Академия ФСО России, РФ, г. Орёл

E-mail: ksw66@yandex.ru

Создание системы мониторинга для исследования и обеспечения качественной эксплуатации мультисервисной сети связи (МСС) требует разработки методики статистической оценки неоднородности параметров, входящих в модели оценки эксплуатационной надёжности и отказоустойчивости МСС. Для оценки показателей эксплуатационной надёжности и отказоустойчивости МСС в целом, необходимо учесть, что элементы МСС содержат большое количество сетевых устройств j-го типа (j=), и взаимодействие между элементами МСС может быть реализовано за счёт применения сетевых устройств различных типов.

Рассмотрим информацию о надёжности сетевых устройств, используемых в МСС. Одна из особенностей этой информации состоит в её разнородности. Исходя из этого, подход к построению методики, позволяющей учесть неод­нородность характеристик эксплуатационной информации, заключаются в следующем.

Предположим, что в МСС имеется случайный набор из N-партий сетевых устройств одного типа, применяемых в её элементах, каждый из которых имеет свои показатели надёжности.

Вероятность безотказной работы устройства за время t можно рассчитать, используя формулу полной вероятности [3]:

, (1)

где: P_j(t) — вероятность безотказной работы j₁-ой партии j-го типа сетевого устройства;

q_j1 — доля в общем количестве партий N .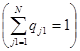

Здесь вероятность P(t), рассматривается как случайная величина, рандомизированная с помощью дискретного распре­деления . В качестве характеристики неоднородности может быть ис­пользована величина, соответствующая дисперсии [1]

. (2)

Следует подчеркнуть, что во время эксплуатации вероятности безотказ­ной работы неизвестны и непосредственно дисперсия (2) не может быть найдена. Поэтому введём интегральную характеристику неоднородности ис­ходной информации по показателям надёжности сетевого устройства j-го типа

. (3)

Величина Н_j позволяет оценить степень неоднородности исходной информации о надёжности с помощью её экстремальных показателей. Заметим, что при t>0 и P₁(t) = P₂(t) =...= P_N’(t), величина Н_j = 0, так как в этом случае D(t) = 0. Рассмотрим представляющий практический интерес случай, когда .

В этом случае будет справедливым неравенство

H < , (4)

где: _mах и _min — наибольшее и наименьшее значение констант Т_j1 соответст­венно и, поскольку , то выполняется неравенство

D(t)<. (5)

В результате, так как , и учитывая что  и , становится возможным получить необходимую оценку степени неоднородности исходной информации о надёжности.

Таким образом, неравенство (4) даёт возможность в совокупности оценить неоднород­ность исходных данных по надёжности j-го типа сетевого устройства МСС исходя из их экстремальных показателей эксплуатационной надёжности.

Заметим, что для наработок до отказа в партии оборудования МСС, имеет место следующая зависимость для определения доли q₀ партии оборудования МСС с интенсивностью отказов l₀:

, (6)

где: l₀ = ;

q₀ — соответствующая доля аппаратуры в совокупности, для которой интенсивность отказов равна l₀.

Поэтому для определения параметров направлений взаимодействия МСС [4] важно определить нижнюю границу интенсивности отказов сетевых устройств i-го типа:

 (7)

а для сетевых устройств i-го типа, произведённых в j-ом году:

, (8)

где: Т_0i — определяется по результатам сбора и анализа статистических наблюдений;

 — количество сетевых устройств i-го типа j-го года производства;

 — общее количество сетевых устройств МСС i-го типа.

Другой важный случай представляется в умении оценивать параметры направлений взаимодействия элементов МСС, образованных неоднородными сетевыми устройствами, поскольку сетевых устройств в элементах МСС с абсолютно одинаковой прочностью на практике не существует [1]. В этих условиях, становится явно выраженной дифференциация сетевых устройств по уровню остаточного ресурса, обусловленная разной интенсивностью расхода ресурса, что связано, с различной эксплуатационной нагрузкой, а также проявляющейся, с течением времени, разницей в начальном запасе ресурса сетевых устройств, заложенной при проектировании и производстве сетевых устройств МСС.

В связи с этим вероятность безотказной (в контексте надёжности) работы МСС, составленной из последовательно соединённых сетевых устройств, ограничивается величиной вероятности безотказной работы наименее прочного узла. В этом состоит сущность принципа «слабого звена», применение которого может упростить задачу определения времени безотказной работы элементов МСС в ряде практических случаев. При этом показатели времени безотказной работы элементов МСС определяются следующими формулами [2]:

, (9)

где:  — значение времени безотказной работы элемента МСС, состоящего из сетевых устройств различной прочности;

 — значение времени безотказной работы элемента МСС;

J — количество элементов МСС.

Для принятия решения о методике расчёта времени безотказной работы (точным или приближённым методом) необходимо воспользоваться количественным критерием степени равнопрочности системы.

Предположим, что  — результаты оценивания времени безотказной работы Z₁-го типа сетевых устройств, образующих МСС. Тогда

, , соответственно, выборочные среднее и дисперсия случайной выборки оценок времени безотказной работы.

При случайном рассеивании оценок  относительно среднего, нормально распределённая случайная величина  с большой вероятностью принимает значения, близкие к своему математическому ожиданию , что выражается правилом сигм [2]:

, (10)

причём правило трёх сигм используется наиболее часто. В соответствии с этим правилом система считается равнопрочной если результаты оценивания остаточного ресурса её сетевых устройств находятся в промежутке . В противном случае система не считается равнопрочной, и для оценки эксплуатационной надёжности направления связи МСС необходимо уметь определять среднюю групповую интенсивность отказов физических и логических каналов связи и узлов МСС по данным о числе отказов и суммарных наработках z₁ типов сетевых устройств, полученным на этапе эксплуатации при помощи средств мониторинга. Тогда усреднённая групповая интенсивность отказов сетевых устройств, образующих однотипные физические и логические каналы связи, для экспоненциального распределения оценивается по формуле

, (11)

где: l_i — интенсивность отказов i-ro типа сетевых устройств.

Формула (11) получена исходя из предположения, что (t) является случайной величиной, а P_i – вероятность того, что она принимает значение l_i. В каче­стве оценок интенсивностей отказов в данном случае примем оценки, получен­ные с применением метода максимального правдоподобия для изделий i-го типа

, (12)

а для средней групповой

 (13)

где: r_i — число отказов сетевых устройств i-ro типа;

T_i — их суммарная наработка, i=();

z₁ — количество типов сетевых устройств, образующих направления (физические и логические каналы) связи и узлы МСС.

Тогда для "t > 0 становится возможным экстраполировать среднюю групповую интенсивность отказов

  (14)

где:  находится с помощью (12).

Таким образом, полученные методики оценки неоднородности исходных данных по формулам (8) и (14) позволяют получить оценку средней групповой интенсивности отказов сетевых устройств, образующих направления и узлы МСС и могут быть использованы в качестве исходных данных для оценки эксплуатационной надёжности направлений и узлов МСС.

Список литературы: 1.    Байхельт Ф., Франкен П. Надёжность и техническое обслуживание. Математический подход. М.: Радио и связь, 1988. — 392 с.2.    Барзелович Е.Ю. Модели технического обслуживания сложных систем. М.: Машиностроение, 1986. — 397 с. 3.    Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и их инженерное приложение. М.: Наука, 1991. — 215 с.4.    Рябинин И.А. Основы теории и расчёта надёжности судовых электроэнергетических систем. 2-е изд. Л.: Судостроение, 1971. — 456 с.