ОБ  ИСПОЛЬЗОВАНИИ  ВЕЩЕСТВ  С  МЕЗОСКОПИЧЕСКИМ  ФАЗОВЫМ  ПЕРЕХОДОМ  В  ТЕПЛОТЕХНИЧЕСКИХ  УСТРОЙСТВАХ

Касымов  Аскар  Багдатович

PhD   докторант,  Казахский  национальный  технический  университет  имени  К.И.  Сатпаева,  Республика  Казахстан,  г.  Алматы

E -mail:  festland2@yandex.kz

Курлапов  Лев  Иванович

д-р  физ.-мат.  наук,  профессор,  Казахский  национальный  технический  университет  имени  К.И.  Сатпаева,  Республика  Казахстан,  г.  Алматы

E -mail:  lkurlapov@yandex.ru

В  циклах  тепловых  машин,  как  и  других  теплотехнических  устройствах,  обычно  подразумевается  использование  веществ  (рабочих  тел)  с  неизменными  физическими  свойствами.  Цель  настоящего  сообщения  сотоит  в  том,  чтобы  привлечь  внимание  на  тот  факт,  что  использование  рабочих  тел,  в  которых  в  процессе  работы  устройства  происходит  мезоскопический  фазовый  переход,  можно  рассматривать  в  качестве  пути  повышения  эффективности  устройств. 

Важное  место  в  науке  занимает  цикл  Карно.  На  основе  этого  цикла  в  термодинамике  разработан  мощный  метод  сложных  процессов,  на  основе  этого  цикла  была  введена  энтропия,  цикл  Карно  является  недостижимым  пределом  по  КПД  для  создателей  тепловых  машин.  Уникальность  этого  цикла  заключается  в  том,  что  это  единственно  возможный  цикл,  который  осуществляется  только  с  двумя  термостатами:  один  термостат  в  качестве  нагревателя,  а  второй  —  в  качестве  холодильника  (теплоприёмника  с  постоянной  температурой).  Кроме  идеализации  этого  цикла,  связанного  с  допущениями  об  обратимости  всех  процессов  в  нём,  в  нём  особое  значение  имеет  принимаемая  по  умолчанию  модель  рабочего  тела,  которое  не  изменяет  своих  свойств,  т.  е.  не  изменяется  ни  в  количественном,  ни  в  качественном  отношении.  С  точки  зрения  статистической  термодинамики  это  соответствует  ограничению  в  иерархии  статистических  ансамблей  каноническим  ансамблем  [7]. 

В  настоящее  время  наблюдается  повышение  интереса  к  циклу  Стирлинга  и  тепловыми  машинами,  работающими  на  этом  цикле.  Это  в  определённой  мере  обусловлено  возрастающими  требованиями  к  экологической  чистоте  современных  тепловых  машин.  В  цикле  Стирлинга  за  всё  время  работы  отсутствуют  выбросы  рабочего  тела  в  окружающую  среду,  что  отвечаем  всем  требованиям  к  зелёным  технологиям  [8].  С  точки  зрения  физики  процессов  в  цикле  Стирлинга  можно  использовать  дорогостоящее  рабочее  тело  и  даже  опасное  при  его  попадании  в  окружающую  среду.  В  связи  с  этим  можно  ставить  задачу  увеличения  его  эффективности  за  счёт  применения  в  качестве  рабочего  тела  специально  синтезированное  пусть  даже  токсичное  вещество.  Этими  веществами  могут  быть  вещества,  в  которых  при  таких  условиях  их  использования,  когда  это  вещество  претерпевает  мезоскопический  фазовый  переход,  важное  место  будут  занимать  тепловые  явления. 

Свойства  такого  вещества  —  рабочего  тела  существенно  изменяются  при  незначительных  изменениях  внешних  макропараметров,  что  проявляется  в  изменении  фактора  сжимаемости  [2;  4].  Барическая  зависимость  фактора  сжимаемости,  расчитанная  с  учётом  кластерного  состава  при  соответствующих  условиях  отображена  на  рис.  1.

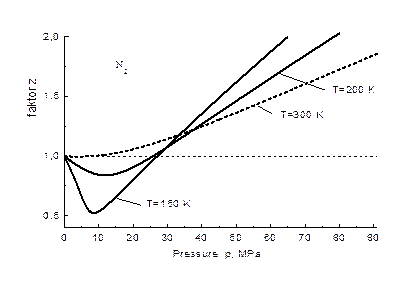
Рисунок  1.  Фактор  сжимаемости    при  различных  давлениях  и  температурах  (справочные  данные  взяты  из  [1])

Как  видно  из  рисунка  1,  барическая  зависимость  существенно  зависит  от  температуры  и  имеет  нерегулярный  характер.  Переход  кривых  через  единицу  не  говорит  о  том,  что  данный  газ  является  идеальным  газом.  В  кластерной  модели  это  объясняется  тем,  что  две  причины,  приводящие  к  изменению  фактора  сжимаемости,  взаимно  компенсируются  [6].

Изменения  свойств  газа  особенно  заметны  в  околокритической  области  температур  и  давлений.  Как  показано  в  ряде  работ,  при  таких  условиях  может  наблюдаться  мезоскопический  фазовый  переход  [3;  5;  6].  Это  явление  наблюдается  как  промежуточное  динамически  равновесное  состояние  между  двумя  агрегатными  состояниями.  Промежуточность  его  заключается  в  том,  что  в  нём  сочетаются  особенности  фазового  перехода  первого  рода  —  выделение  или  поглощение  энергии  фазового  перехода  и  особенности  фазового  перехода  второго  рода:  он  происходит  во  всём  объёме  без  образования  границы  раздела  фаз.  Выявление  областей,  где  происходит  мезоскопический  фазовый  переход  невозможно  без  данных  о  кластерном  составе  рабочего  вещества.  Такие  данные  для  примера  приведены  на  рис.  2  и  3.

Рисунок  2.  Распределение  кластеров  в  азоте  по  размерам  при  различных  давлениях  (точки  —  расчет  по  формулам  экспоненциального  распределения,  линии  —  расчеты  по  формуле    с  использованием  констант  взятых  из  [1])

Как  видно,  в  этом  газе  при  данных  условиях  могут  существовать  кластеры  достаточно  больших  размеров.  Причем,  в  неизотермических  условиях,  которые  представляют  особый  интерес  в  теплотехнических  устройствах,  при  переходе  из  областей  с  одной  температурой  в  область  с  другой  температурой  происходит  перестройка  кластерной  структуры,  т.  е.  эволюция  кластерного  состава.  На  рисунке  3  такие  данные  приведены  с  использованием  распределений  из  рисунка  2  при  различных  температурах.

Рисунок  3.  Эволюция  кластерного  состава  в  азоте  при  давлении  16  МПа:  зависимость  концентраций  молекулярно-кластерных  субкомпонентов:  от  концентрации  молекул    до  концентрации  кластеров    ( справочные  данные  взяты  из  [1])

Как  видно  из  рисунка  3,  концентрация  молекул,  как  и  ожидалось,  растёт  с  ростом  температуры.  Концентрация  других  кластеров  меняется  нерегулярным  образом.  Это  связано  с  тем,  что  распад  одних  кластеров  может  увеличивать  концентрацию  других.  В  частности  концентрация  димеров  и  тримеров  при  низкой  температуре  растёт  за  счёт  распада  более  крупных  кластеров,  а  при  высокой  –  уменьшается  вследствие  их  распада  и  образования  молекул.

С  точки  зрения  теплотехники,  особое  значение  имеет  факт  поглощения/выделения  энергии,  которым  сопровождается  эволюция  кластерного  состава.  Примененные  в  данной  работе  расчетные  схемы  позволяют  прогнозировать  и  управлять  этими  процессами  в  теплотехнических  устройствах.  Из  приведенных  отрывочных  данных  следует  необходимость  целенаправленного  изучения  свойств  мезоскопических  систем.

Список  л итературы:

1.Варгафтик  Н.Б.  Справочник  по  теплофизическим  свойствам  газов  и  жидкостей.  М.:  Наука.  1972.  —  720  с. 

2.Курлапов  Л.И.,  Касымов  А.Б.  Мезоскопические  свойства  молекулярно-кластерной  смеси  азота.  //  Труды  международной  научно-практической  конференции  «Информационные  и  телекоммуникационные  технологии:  образование,  наука,  практика».  Алматы.  2012.  —  С.  538—541. 

3.Курлапов  Л.И.,  Касымов  А.Б.  Мезоскопический  фазовый  переход  в  молекулярно-кластерных  смесях  плотных  газов.  Сборник  тезисов  Международного  научного  симпозиума  «Новые  концепции  в  физике  конденсированного  состояния».  Алматы,  17—18  ноября  2014.  —  С.  59.

4.Курлапов  Л.И.,  Касымов  А.Б.  Особенности  физических  свойств  молекулярно-кластерной  смеси  криптона.  //  Труды  II  Международной  научной  конференции  «Высокие  технологии  —  залог  устойчивого  развития»  I  том.  Алматы:  КазНТУ  им.  К.И.  Сатпаева,  2013.  —  312  с.  —  С.  132—135.

5.Курлапов  Л.И.  Мезоскопия  кластерных  газов.  //  ЖТФ.  —  Т.  75,  —  №  8.  —  2005  —  С.  136—139.

6.Курлапов  Л.И.  Физическая  кинетика  мезоскопических  систем.  От  материальной  точки  к  мезоскопической  частице.  Монография.  LAP  LAMBERT  Academic  Publishing.  —  2011.  —  116  с.  —  ISBN-13:  978-3-8454-3722-4;  ISBN-10:  3845437227. 

7.Румер  Ю.Б.,  Рывкин  М.Ш.  Термодинамика,  статистическая  физика  и  кинетика.  М:  Наука.  1972.  —  400  с.

8.Уокер  Г.  Двигатели  Стирлинга.  М.:  Машиностроение.  1985.  —  408  с.