АНАЛИТИЧЕСКОЕ  МОДЕЛИРОВАНИЕ  ДЕЛОВЫХ  ПРОЦЕССОВ  КАК  СИСТЕМ  МАССОВОГО  ОБСЛУЖИВАНИЯ  ДЛЯ  ОЦЕНКИ  ИХ  ПОКАЗАТЕЛЕЙ  ЭФФЕКТИВНОСТИ

Галиуллина  Альбина  Фаритовна

аспирант  Уфимского  государственного  авиационного  технического  университета,  РФ,  г.  Уфа

E-mail:  GAF1205@yandex.ru

Введение

Аналитическая  модель  —  это  математическое  описание  структуры  и  процесса  функционирования  системы,  а  также  методика  определения  показателей  ее  эффективности.  Такая  модель  позволяет  быстро  и  с  высокой  точностью  характеризовать  поведение  системы  [1].

Наиболее  эффективны  и  наглядны  аналитические  модели  при  описании  функционирования  систем  массового  обслуживания  (СМО).  Системы  массового  обслуживания  —  это  такие  системы,  в  которые  в  случайные  моменты  времени  поступают  заявки  на  обслуживание,  при  этом  поступившие  заявки  обслуживаются  с  помощью  имеющихся  в  распоряжении  системы  каналов  обслуживания.  Для  полного  описания  СМО  и  постановки  задачи  исследования  необходимо  определить  структуру  системы  и  дисциплину  (правила)  обслуживания,  а  также  показатели  качества  и  эффективности  обслуживания,  т.  е.  некоторые  числовые  показатели,  по  значению  которых  можно  было  бы  судить  о  качестве  и  эффективности  функционирования  исследуемой  СМО  [1].

Существует  множество  задач  в  управлении  деловыми  процессами,  которые  можно  представить  именно  как  систему  массового  обслуживания.  В  качестве  такого  делового  процесса  может  быть  представлен  процесс  предоставления  государственных  услуг,  который  можно  рассмотреть  в  качестве  СМО.  В  данной  статье  рассмотрено  аналитическое  моделирование  системы  массового  обслуживания  на  примере  процесса  предоставления  государственных  услуг.

1.  Разработка  аналитической  модели  СМО  процесса  предоставления  государственных  услуг  в  программном  пакете  MATLAB

Рассмотрим  одноканальную  СМО  с  отказами,  которая  представляет  собой  окно  Пенсионного  фонда,  в  котором  предоставляют  государственную  услугу  по  установлению  федеральной  социальной  доплаты  к  пенсии.  Заявка  —  гражданин,  обратившийся  в  Пенсионный  фонд  в  момент,  когда  окно  занято  —  получает  отказ  в  обслуживании.  Интенсивность  потока  заявок  λ=1  (одна  заявка  в  10  минут).  Средняя  продолжительность  обслуживания  (предоставления  государственной  услуги)  —  17  минут.  Поток  заявок  (граждан)  и  поток  обслуживания  (предоставления  государственных  услуг)  являются  простейшими. 

Требуется  определить  в  установившемся  режиме  предельные  значения:

а.   относительной  пропускной  способности  q; 

б.  абсолютной  пропускной  способности  А; 

в.   вероятности  отказа  P_otk; 

г.   сравнить  фактическую  пропускную  способность  СМО  с  номинальной,  которая  была  бы,  если  бы  процесс  предоставления  государственной  услуги  требовал  точно  17  минут  и  граждане  обращались  в  Пенсионный  фонд  один  за  другим  без  перерыва;

д.  найти  статистические  оценки  характеристик  СМО  (количество  обратившихся  в  Пенсионный  фонд  граждан,  количество  граждан,  получивших  государственную  услугу,  количество  отказов  в  обслуживании  за  время  работы  системы)  при  продолжительности  работы  СМО  —  80  минут. 

Время  обслуживания  определяется  как  случайная  величина,  распределенная  по  закону  Пуассона.

Введем  обозначения  параметров  СМО,  которые  известны  из  условия  задачи:

TFlow  =  0.1;  %  Интенсивность  обращения  граждан  для  получения  государственной  услуги

TServe  =  17;  %  Среднее  время  обслуживания  —  предоставления  государственной  услуги  (минуты)

TWork  =  80;  %  Продолжительность  работы  СМО  (минуты)

В  открытом  M-File  в  MATLAB  опишем  переменные,  необходимые  для  решения  поставленной  задачи:

z  =  [0  0  0];  %  Заявки  системы  (всего  обратившихся  за  услугой  граждан  за  время  работы  СМО;  граждане,  получившие  государственную  услугу;  отказано  в  обслуживании)

smo_q  =  0;  %  Относительная  пропускная  способность  СМО

smo_a  =  0;  %  Абсолютная  пропускная  способность  СМО

smo_n  =  0;  %  Номинальная  пропускная  способность  СМО

p_fail  =  0;  %  Вероятность  получения  отказа  СМО

mu  =  1/TServe;  %  Интенсивность  потока  обслуживания  граждан

После  объявления  переменных,  запишем  формулы  для  расчета  п.  а)—г):

smo_q  =  mu/(TFlow+mu);  smo_a  =  mu*TFlow/(mu+TFlow);

smo_n  =  mu;  p_fail  =  1-smo_q.

Для  статистического  моделирования  (п.д)  необходимо  составить  процедуру.  Переменной  z(1)  присваивается  значение  поступивших  заявок,  переменной  z(3)  –  число  отказов  в  обслуживании)  и  z(2)  —  число  обслуженных  заявок.  Функция  n  служит  для  моделирования  процесса  поступления  заявок  и  инициализируется  как  случайная  величина,  распределенная  по  закону  Пуассона  с  математическим  ожиданием  10  (мин.).  Отсчет  времени  ведем  в  минутах  и  моделируем  как  цикл  с  параметром  t.  Т.  к.  в  среднем  поступает  одна  заявка  в  10  минут,  то  событие  n=0  означает,  что  заявка  поступила  в  СМО.  Время  обслуживания  определяется  переменной  t,  которая  инициализируется  как  случайная  величина,  распределенная  по  закону  Пуассона  с  математическим  ожиданием  17  (мин.).  Время  окончания  обслуживания  заявки  хранится  в  переменной  t_okon.  Если  t=0,  то  канал  обслуживания  свободен,  и  заявка,  поступившая  в  СМО,  будет  обслужена.  Если  t>0,  то  поступившая  заявка  получает  отказ,  что  фиксируется  как  z(3)=z(3)+1,  а  величина  t  убывает  с  каждым  циклом  на  одну  минуту  (t=t–1). 

for  (y=1:2) 

  z  =  [0  0  0];

  t  =  0;  n  =  0;

  for  (i=1:TWork)

  if  (n==0)  %  поступление  заявки

  z(1)=z(1)+1;  n=poissrnd(1/Tflow);

  if  (t==0)  %  заявка  поступает  на  обслуживание

  z(2)=z(2)+1;  t=poissrnd(Tserve);

  else  %  система  занята,  заявка  отклоняется

  z(3)=z(3)+1;

  end

  end  %  обслуживание  заявки

if  (t>0)  t=t-1;

  end

if  (n>0)  n=n-1;

end

  end.

2.  Результаты  аналитического  моделирования

Для  того,  чтобы  вывести  результаты  моделирования,  воспользуемся  средой  GUIDE,  входящей  в  состав  MATLAB,  которая  позволяет  разработать  интерфейс  для  аналитической  модели.  Результаты  моделирования  представлены  на  рис.  1.

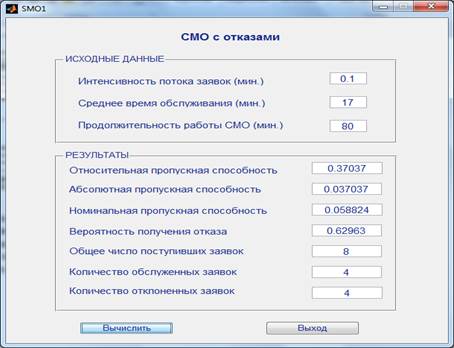
Рисунок  1.  Результаты  моделирования  СМО

Таким  образом,  по  результатам  аналитического  моделирования  процесса  предоставления  государственных  услуг  в  Пенсионном  фонде  вычислены  относительная  и  абсолютная  пропускные  способности  системы,  которые  равны  0,37037  и  0,037037,  соответственно.  Также  вычислена  номинальная  пропускная  способность,  которая  равна  0,058824,  и,  которая  была  бы,  если  бы  процесс  предоставления  государственной  услуги  каждому  обратившемуся  в  Пенсионный  фонд  гражданину  требовал  точно  17  минут  и  граждане  обращались  за  услугой  один  за  другим  без  перерыва. 

Кроме  того,  в  результате  аналитического  моделирования  (при  продолжительности  работы  СМО  —  80  минут)  определены  статистические  оценки  характеристик  СМО,  которые  показали,  что  общее  количество  обратившихся  в  Пенсионный  фонд  граждан  (за  время  моделирования)  составляет  8  человек.  Из  8-и  человек  4  человека  сразу  же  были  обслужены.

3.  Вывод

В  результате  аналитического  моделирования  процесса  предоставления  государственных  услуг  были  определены  основные  показатели  эффективности. 

Если  сравнить  фактическую  и  номинальную  пропускные  способности  СМО,  то  оказывается,  что  номинальная  в  1,6  раза    больше  фактической  пропускной  способности,  вычисленной  с  учетом  случайного  характера  потока  заявок  и  времени  обслуживания.  Это  говорит  о  том,  что  система  функционирует  недостаточно  эффективно.  Для  повышения  эффективности  работы  Пенсионного  фонда  следует  установить  более  оптимальные  параметры  СМО  (сократить  фактическое  время  обслуживания  граждан  или  добавить  еще  один  канал  обслуживания,  т.  е.  дополнительное  окно). 

Список  литературы:

1.Петухов  О.А.,  Морозов  А.В.,  Петухова  Е.О.  Моделирование:  системное,  имитационное,  аналитическое:  Учебное  пособие.  СПб.:  издательство  СЗТУ,  2008.  —  288  с.