Статья опубликована в рамках: XI Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 07 апреля 2014 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОБЗОР МЕТОДА ИМИТАЦИИ ОТЖИГА И ЕГО МОДИФИКАЦИЙ В АСПЕКТЕ ПРИМЕНИМОСТИ К РЕШЕНИЮ ЗАДАЧИ КОМПЛЕКТАЦИИ ВЫЧИСЛИТЕЛЬНОЙ СИСТЕМЫ МИНИМАЛЬНОЙ СТОИМОСТИ В УСЛОВИЯХ ДЕФИЦИТА ВРЕМЕНИ
Троценко Роман Владимирович
канд. техн. наук, доцент инженерно-технологической академии Южного Федерального Университета, РФ, г. Таганрог
" target="_blank">roman.trotsenko@gmail.com
Посашенко Александр Владимирович
учащийся магистратуры инженерно-технологической академии Южного Федерального Университета, РФ, г. Таганрог
E -mail:
Одной из формулировок задачи о комплектации вычислительной системы (ВС) является задача о комплектации ВС минимальной стоимости, сформулированная и решенная А.Б. Барским [1—3]. В общем случае задача имеет следующий вид: «для заданного комплекса информационно и по управлению взаимосвязанных задач, заданной архитектуры вычислительной системы, а также заданного ограничения на допустимое время вычислительного процесса выбрать комплектацию ВС минимальной стоимости» [1]. Под стоимостью понимают вес каждого типа процессоров, который необходимо учитывать при выборе оптимальной комплектации.
Формально задача о нахождении комплектации ВС минимальной стоимости представлена следующим образом: среди возможных вариантов ![]() построения ВС, способной выполнить данный алгоритм, который представлен информационным графом G=(X,P,I,Г), за заданное время T≥Tкр, выбрать систему минимальной стоимости
построения ВС, способной выполнить данный алгоритм, который представлен информационным графом G=(X,P,I,Г), за заданное время T≥Tкр, выбрать систему минимальной стоимости
|
|
(1) |
где: множество ![]() вершин графа соответствует множеству операторов алгоритма, множество
вершин графа соответствует множеству операторов алгоритма, множество ![]() определяет время выполнения каждого оператора, соответствующего вершине, множество Г определяет дуги, отражающие связь между операторами по информации, множество
определяет время выполнения каждого оператора, соответствующего вершине, множество Г определяет дуги, отражающие связь между операторами по информации, множество ![]() — номера типов процессоров, за которыми закреплен j-й оператор,
— номера типов процессоров, за которыми закреплен j-й оператор, ![]() — соответственно «стоимость» i-го процессора.
— соответственно «стоимость» i-го процессора.
Задача комплектации ВС минимальной стоимости относится к задачам комбинаторной оптимизации и является NP-сложной. Для этого класса задач одной из весомых проблем становится время получения решения.
Следует отметить, что существует аналитический метод решения задачи комплектации ВС, который был предложен А.Б. Барским и подробно описан в [1]. Метод позволяет найти глобальный минимум целевой функции и представляет собой комбинацию метода ветвей и границ с участками полного перебора. Обладая несомненным преимуществом — возможностью получить точное решение – тем не менее, является весьма трудозатратным [1], в связи с чем может потребоваться неприемлемое время для нахождения решения. По словам автора аналитического метода, последний может находить применение на этапах планирования ВС, когда ограничение на время поиска решения не налагается.
Одним из наиболее часто используемых численных методов является имитация отжига или ее различные адаптации (в комбинации с генетическими алгоритмами и методами локального поиска). Преимущество ГА, несмотря на многочисленные публикации в этой области, является по-прежнему спорным. Это, прежде всего, связано с тем, что для любого ГА необходима настройка параметров и, кроме того, ГА изначально не были ориентированы на решение задач оптимизации [4].
Имитация отжига, в отличие от ГА, является универсальным методом поиска глобального минимума целевой функции и имеет как достоинства, так и недостатки [5]. К достоинствам относят: возможность поиска решений для сложных нелинейных задач, возможность работы с данными с обилием шумов и помех; способность выхода из локальных минимумов, универсальность метода, относительную легкость модификации, адаптации и технической реализации. Среди недостатков, как правило, отмечают следующие: необходимость адаптации параметров для каждой конкретной задачи, зависимость качества решения от времени его получения.
В связи с вопросом глобальной сходимости выделяют три разновидности имитации отжига, каждая из которых связана с использованием определенного закона изменения температуры [6]:
1. Логарифмический: ![]() ;
;
2. Коши: ![]() ;
;
3. Экспоненциальный: ![]() .
.
Для логарифмического изменения температуры была доказана глобальная сходимость алгоритма, доказательство опирается на распределение Гаусса. Отжиг Коши также имеет доказательство глобальной сходимости, опирающееся на распределение Коши. Для экспоненциального закона изменения температуры было проведено доказательство сходимости для частного случая [4].
Для Больцмановской схемы имитации отжига и схемы Коши доказано достижение глобального минимума (для ГА аналогичного доказательства не существует), но в условиях ограничений на время получения решения эти схемы обладают существенным недостатком: вычисления занимают значительное время. В связи с этим часто используют так называемые схемы «тушения», при которых ускоряется понижение температуры, при этом возможен вариант нахождения субоптимального решения.
В аспекте минимизации времени решения задачи целесообразно выделить подход, при котором метод имитации отжига распараллеливается между процесорными устройствами (ПУ). Следует отметить, что имитация отжига является последовательным методом, что в некоторой мере затрудняет распараллеливание, но тем не менее, были разработаны подходы, позволяющие путем распараллеливания вычислений добиться улучшения времени поиска решения.
В открытых источниках упомянуты следующие основные подходы к распараллеливанию имитации отжига [7].
Первый способ — параллельный запуск алгоритма имитации отжига — предполагает вычисление глобального минимума целевой функции одновременно на нескольких ПУ с последующим выбором лучшего решения управляющим узлом. В этом случае очевидна возможность использования методов «тушения» с последующим выбором наилучшего решения из числа полученных, возможно, субоптимальных решений.
Второй способ — параллельный запуск алгоритма с обменом результатами — предполагает по истечении определенного количества итераций обмен между ПУ и выбор лучшего результата для продолжения вычислений. Этот подход базируется на установленном факте о том, что результат и время получения решения имитации отжига зависят от выбранной начальной точки.
Третий способ — разбиение пространства решений на области — предполагает запуск последовательного алгоритма имитации отжига в каждой из выделенных областей решений с выбором наилучшего решения по окончании вычислений.
Также с целью улучшения временных показателей работы имитации отжига, было разработано немало гибридных методов, зачастую представляющих собой комбинацию имитации отжига и ГА. Ниже приводятся примеры разработок с кратким описанием.
Авторы Sirag и Weisse [8] провели совмещение нескольких генетических операторов в «объединенный термодинамический оператор» для решения задачи о коммивояжере. Объединенный оператор применяется к двум родителям с целью воспроизведения одного потомка. При высоких температурах, потомок имеет большую степень отличия от родителей, при низких температурах потомок в большей степени является повторением одного или обоих родителей. Подход не имеет гарантированной сходимости.
В работе [10] описан ряд стратегий для решения задачи о коммивояжере. Простейшей стратегией является запуск нескольких имитаций отжига с инверсией городов в качестве оператора ближайшего соседа. Периодически производится сравнение текущих решений двух процессоров, и худшее текущее решение заменяется на лучшее. Следующая стратегия использует подобную селекцию по окончании отжига, затем производится рестарт имитации отжига на высокой температуре. Каждый цикл имитации отжига назван «жизненным циклом». Третья стратегия предполагает в конце каждого жизненного цикла операцию скрещивания. В результате сравнения трех стратегий с классической имитацией отжига, авторы делают вывод о том, что наилучшие результаты в аспекте времени вычисления дает стратегия, предполагающая наличие операции скрещивания.
Одной из интересных разработок, для которой было проведено распараллеливание, является параллельный рекомбинантный алгоритм имитации отжига (Parallel Recombinative Simulated Annealing) [9] .
Основной идеей PRSA является следующее: несколько копий имитации отжига запускается параллельно, в качестве оператора генерации нового решения используется оператор мутации, скрещивание используется для комбинации независимых решений.
Процедура генерации популяции заключается в следующем:
1. Повторить n/2 раз, где n — размер популяции:
· выбрать случайным образом двух родителей из n элементов популяции;
· посредством скрещивания и мутации произвести двух потомков;
· произвести одну или две Больцмановских проб между детьми и родителями;
· перезаписать родителей победителями Больцмановских проб.
2. Понизить температуру T.
Больцмановская проба по сути является соревнованием между i-м и j-м решением, где i-й элемент выигрывает с вероятностью ![]() (также может быть использован критерий Метрополиса
(также может быть использован критерий Метрополиса 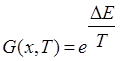 ).
).
Подводя итоги исследования метода имитации отжига и его модификаций в аспекте решения задачи комплектации ВС в условиях дефицита времени, можно сделать следующие основные выводы:
· централизованный метод имитации отжига, обладая свойством нахождения глобального экстремума целевой функции, в условиях дефицита времени на получение решения неэффективен, в связи с чем перспективными представляются исследования в области параллельных вычислений;
· распараллеливание имитации отжига существенно улучшает время поиска решения;
· комбинирование имитации отжига с другими методами поиска также улучшают время получения результата, в том числе и для централизованной реализации алгоритма. В связи с этим представляется целесообразным использование комбинированных методов и алгоритмов в параллельных вычислениях.
Следует отметить, что, являясь многообещающим подходом, параллельные адаптации имитации на настоящее время недостаточно исследованы на предмет влияния накладных расходов на коммуникацию между ПУ на эффективность вычислений. Также в открытых источниках не представлены численные оценки зависимости качества получаемых решений от количества ПУ и затраченного на поиск решения времени. Недостаток результатов в этих областях является определяющим для дальнейших исследований в области применимости и эффективности имитации отжига для решения задачи комплектации ВС в условиях дефицита времени.
Список литературы:
1.Барский А.Б. Параллельные процессы в вычислительных системах: планирование и организация. М.: Радио и связь, 1990.
2.Барский А.Б. Планирование параллельных вычислительных процессов. М.: Машиностроение, 1980. — 912 с.
3.Барский А.Б. Потоковая обработка информации в ВС на асинхронном решающем поле//Вопросы кибернетики. Проблемы организации высокопроизводительных ЭВМ/НС по комплексной проблеме «Кибернетика» АН СССР. М., 1984. — С. 119—141.
4.Azencott R.. Sequential simulated annealing: speed of convergence and acceleration techniques. Simulated Annealing: Parallelization Techniques, Wiley and Sons, New York, 1 (1992).
5.Boseniuk T., W. Ebeling, Optimisation of NP complete problems by oltzmann-Darwin strategies including life cycles, Europhysics Letters, 6(2), 1988, — p. 107—112.
6.Busetti F., Simulated annealing overview. 2003. [Электронный ресурс] — Режим доступа. — URL: http://citeseer.uark.edu:8080/citeseerx/viewdoc/summary;jsessionid=9F958F3AD8ACB341A84315A737883592?doi=10.1.1.66.5018)
7.Ingber L.. Very fast simulated reannealing. Mathematical Computer modeling, 12,967. 1989
8.Janaki Ram D., Sreenivas T.H., Ganapathy Subramaniam K. Parralel Simulated Annealing Algorithms//J. of parallel and distributed computing. — 1996. — № 37, — P. 207—212.
9.Mahfoud S.W., D.E. Goldberg. Parallel Recombibative Simulated Annealing: A Genetic Algorithm. Illinois Genetic Algorithms Laboratory, University of Illinois at Urbana-Champaign. 1995.
10.Sirag D.J., P.T. Weisser, Toward a n-nified thermodynamic genetic operator. Genetic Algorithms and their Applications: Proceedings of the Second International Conference on Genetic Algorithms, 1987, — p. 116—122.
дипломов


Оставить комментарий