МОДУЛЯРНЫЕ  ПРЕОБРАЗОВАНИЯ  В  ВЕЙВЛЕТ-АНАЛИЗЕ  СИГНАЛОВ  ДЛЯ  РАСПОЗНАВАНИЯ  РЕЧИ

Гапочкин  Артём  Владимирович

аспирант  Северо-Кавказского  федерального  университета,  РФ,  г.  Ставрополь

E-mail:  Warrior_555@rambler.ru

В  большинстве  существующих  систем  распознавания  и  анализа  речи  звук  рассматривается  как  поток  векторов,  элементами  которых  являются  некоторые  частотные  характеристики.  Известно,  что  речь  человека  характеризуется  высокой  степенью  изменчивости,  поэтому  различные  акустические  реализации  одних  и  тех  же  речевых  единиц  (например,  фонем)  значительно  различаются.  Поэтому  обработка  речи  в  реальном  времени  с  использованием  последовательных  алгоритмов  требует  вычислительных  средств  с  высоким  быстродействием  [1]. 

Кроме  того,  важно,  результатами  каких  преобразований  являются  элементы  векторов,  которыми  представлена  речь.  Для  задачи  идентификации  необходимо  получить  наиболее  четкую  спектральную  картину  произнесенной  фразы,  поэтому  здесь  в  основном  применяется  преобразование  Фурье.  Основным  недостатком  этого  метода  является  то,  что  он  применим  лишь  для  анализа  стационарных  сигналов.  Речь  же  представляет  собой  нестационарный  сигнал.  Переход  к  оконному  преобразованию  Фурье  приводит  к  сильной  зависимости  частотных  характеристик  от  параметров  окна  [1].

Поэтому  в  последнее  время  используется  альтернативный  подход  к  решению  задачи  анализа  нестационарных  сигналов,  одним  из  вариантов  которого  является  вейвлет-анализ  [2,  3,  4,  5].

Вейвлет-анализ  есть  логическое  продолжение  оконного  преобразования  Фурье.  Однако  если  в  случае  Фурье  анализа  в  качестве  базиса  используются  гармонические  функции,  бесконечные  во  времени,  то  для  вейвлет-анализа  используются  функции  в  виде  «маленькой  волны»,  которые  ограниченны  по  времени.

Вейвлет-анализ  осуществляет  многомасштабный  анализ,  который  представляет  собой  последовательное  представление  исследуемой  функции  через  иерархические  вложенные  подпространства  V_m,  которые  не  пересекаются  и  дают  в  пределе  L²(R)  —  пространство  квадратично  суммированных  последовательностей  бесконечной  длинны  [2,  3]

  ,  (1)

  .

Если  осуществлять  анализ  функции  вплоть  до  некоторого  масштаба  m,  то  f(x)  будет  представлена  суммой  грубой  аппроксимации    и  множества  деталей  e_j,  принадлежащих  пространству  W_j,  такому  что

;

;

;  (2)

.

Одним  из  важных  моментов  вейвлет-анализа  является  произвольный  выбор  базисной  функции.

На  вход  практически  любой  системы  автоматического  анализа  речевой  информации  поступает  дискретизированный  по  времени  и  квантованный  по  амплитуде  речевой  сигнал.  Для  анализа  дискретной  временной  последовательности  можно  использовать  вейвлет  Хаара  [2].  Для  входного  сигнала,  представленного  массивом  2"  чисел,  вейвлет-преобразование  Хаара  просто  группирует  элементы  по  2  и  образует  от  них  суммы  и  разности.  Группировка  сумм  проводится  рекурсивно  для  образования  следующего  уровня  разложения.  В  итоге  получается  2п  —  1  разность  и  1  общая  сумма.  Но  его  применение  эффективно  в  том  случае,  если  дискретная  временная  последовательность  обладает  резкими  переходами  или  скачками.  По  мимо  вейвлетов  Хаара  существует  еще  ряд  дискретных  вейвлетов,  описанных  в  [3]. 

Так  как  вычисление  коэффициентов  дискретного  вейвлет-преобразования  требует  интенсивных  вычислений,  для  решения  задач  распознавания  речи,  особенно  функционирующих  в  режиме  реального  времени,  требуется  разработка  максимально  эффективных  алгоритмов  для  программных  или  аппаратных  вычислений.  Вычисление  дискретного  вейвлет-преобразования  может  быть  реализовано  по  алгоритму  Малла  с  помощью  КИХ-фильтров,  которые  содержат  только  операции  сложения  и  умножения.

В  качестве  таких  преобразований  можно  использовать  модулярные  преобразования,  а  именно  перевод  чисел  из  системы  остаточных  классов  (СОК)  в  позиционную  систему  счисления  [6].

Пусть  имеется  СОК  с  основаниями  p₁,  p₂  …..p_n,.  Для  этой  системы  определены  ортогональные  базисы  B₁,  B₂,  ….  B_n  с  весами  m₁,  m₂,  …..  m_n.  Пусть  в  этой  системе  своими  остатками  заданно  число  остатками  А=(α₁,  α₂,  …  α_n).  Определим  следующие  константы

q₁  =  p₁m₂;  q₂  =  p₂m₁;  ;  q_n  =  p_n  m_n-(-1)ⁿ;

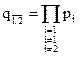
  ;…;  .  (1.1)

Тогда  позиционное  представление  числа  А  можно  вычислить  следующим  образом

;  ;…;,  (1.2)

.  (1.3)

Доказательство  этого  утверждения  основано  на  следующем  обстоятельстве.  Развернем  первое  слагаемо  выражения  (1.3)

.  (1.4)

Величина  есть  первый  ортогональный  базис  B₁.  Остальные  слагаемые  имеют  аналогичную  структуру.

Для  случая,  когда  n  нечетно,  константы    и    имеют  следующий  вид

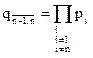;  .  (1.5)

По  аналогии  с  выражением  (1)  можно  считать,  что  каждое  выражения  (1.2.,  1.3)  аппроксимирует  положение  набора  остатков  из  пространства    через  пространство    на  пространство  меньшей  размерности,  определяемое  функцией  y  =  x  mod  p.

Проанализируем  теперь,  как  выполняются  требования,  предъявляемые  к  базисным  функциям  вейвлет-преобразований  для  функции  y  =  x  mod  p  [2,  3].

Ограниченность.  Квадрат  нормы  функции  должен  быть  конечным.

.  (1.6)

Локализация  (локальность).  Функция,  используемая  в  качестве  вейвлета,  должна  быть  локальна  по  частоте  и  во  времени.

Нулевое  среднее.  График  исходной  функции  должен  осцилировать  (быть  знакопеременным)  вокруг  нуля  на  оси  времени  и  иметь  нулевую  площадь

.  (1.7)

Прежде  чем  анализировать  эти  требования,  необходимо  сделать  ряд  замечаний.  Функция  y  =  x  mod  p  кусочно-непрерывна,  причем  на  участках  непрерывности  постоянна,  поэтому  для  вычисления  интеграла  вида    будем  использовать  сумму

,  (1.8)

которая  в  пределе  при  бесконечном  увеличении  числа  делений  n  и  при  бесконечном  уменьшении  наибольшей  из  разностей  (x_k  —x_k-1)  даст  нам  определенный  интеграл  [7].

Для  функции  y  =  x  mod  p:  (-x)  mod  p=(p-x)  mod  p  и    ,  поэтому  условие  ограниченности  в  кольце  по  модулю  выполняется.

Функция  y  =  x  mod  p  локализована  в  частотной  области.  Это  видно  из  графиков,  приведенных  на  рисунке  1.  Причем  основной  лепесток  спектра  для  данной  функции  уже,  чем  у  вейвлета  Хаара.

Функция  y  =  x  mod  p  на  всей  числовой  оси  является  периодичной  с  периодом  р.  Но  если  речь  идет  о  вычислении  в  кольце  по  модулю,  то  ее  можно  считать  ограниченной,  локальной  во  времени.

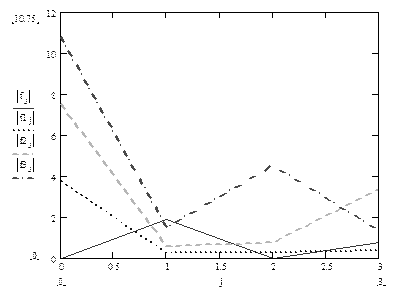
Рисунок  1.  Графики  модуля  спектра  вейвлета  Хаара  и  функции  y  =  x  mod  p  для  различных  р.

где:  f  —  вейвлет  Хаара

f1  —  y  =x  mod  3

f2  —  y  =x  mod  5

f3  —  y  =x  mod  7

Требование  нулевого  среднего  для  функции  y  =  x  mod  p  в  пространстве,  определяемом  выражением  (1),  не  выполняется.  Но  это  требование  выполняется  в  пространстве    при  условии  вычисления  интеграла  (1.7)  через  предел  суммы  (1.8)  с  учетом  замечаний,  изложенных  выше.

Таким  образом,  функция  y  =  x  mod  p  формально  отвечает  требованиям,  предъявляемым  к  вейвлетам  с  учетом  особенностей  выполнения  операций  в  кольце  по  модулю.

В  качестве  примера  приведем  разложение  сигнала,  изображенного  на  рисунке  2. 

Будем  полагать,  что  отсчеты  сигнала  1  ÷  4,  5  ÷  8,  …  13  ÷  16,  представленного  в  виде  вектора  X  =  (6,  4,  13,  5,  9  11,  14,  12,  10,  8,  4,  6,  13,  10,  9,  8)  представляют  собой  остатки  по  модулям  р₁  =  17;  р₂  =  19;  р₃  =  23;  р₄  =  29.

Рисунок  2.  График  исследуемого  сигнала

Данные  модули  выбраны  из  условия

P_{i  min}>{S_i}  для  всех  i,  (1.9)

где:  S_i  —  множество  значений  сигнала.

Для  данной  системы  оснований  значения  весов  будут  следующими:  m₁  =  15,  m₂=14,  m₃  =  4,  m₄  =  6.  Константы  q_i  будут  соответственно  равны:  q₁  =  238,  q₂=285,  q₃  =  138,  q₄  =  116    =  323,    =  667.  Значения  коэффициентов  преобразования  приведены  в  таблице  1.1.

Таблица  1. 

Коэффициенты  модулярного  преобразования

Для  иллюстрации  чувствительности  данных  преобразований  к  небольшим  изменениям  сигнала  внесем  искажения  в  исходный  сигнал:  увеличим  его  четвертый  отсчет  на  2  единицы    =  (6,  4,  13,  5,  9  13,  14,  12,  10,  8,  4,  6,  13,  10,  9,  8)

Значения  коэффициентов  модулярного  преобразования  приведены  в  таблице  2.

Таблица  2. 

Коэффициенты  модулярного  преобразования  искаженного  вектора

Величины  A_i  и  Int_i  введены  для  того,  чтобы  избежать  обработки  больших  абсолютных  значений  Y₁₄.  Кроме  того,  величину  Int_i  можно  интерпретировать  как  постоянную  составляющую  части  сигнала  на  некотором  интервале  анализа,  что  дает  дополнительную  информацию  о  его  свойствах.  Таким  образом,  коэффициенты  разложения  S_i,j,  Y_1,4,  A_i,  Int_i  можно  считать  аппроксимирующими  коэффициентами.

Улучшение  чувствительности  к  малым  изменениям  сигнала  для  такого  преобразования  обеспечивается  за  счет  значительного  изменения  величины  S_i,j  для  близких  в  смысле  евклидового  расстояния  участков  двух  разных  сигналов,  и  величины  A_i  для  участков  двух  разных  сигналов  для  которых  отличие  S_i,j  минимально.  Последнее  утверждение  можно  проиллюстрировать  следующим  примером.

Пусть  для  участков  некоторых  сигналов  S1_1,2=2662,  S1_3,4=2198,  S2_1,2=2663,  S2_3,4=2198.  Тогда  Y1_1,4  mod  R=115657  и  Y2_1,4  mod  R=116324.  Как  видно  из  примера,  разница  между  Y1_1,4  и  Y2_1,4  значительна.

Дисперсия  [8],  рассчитанная  для  различных  методов  анализа  сигналов  приведена  в  таблице  3.

Таблица  3. 

Дисперсия  для  различных  методов  анализа

Оценка  количества  операций  для  вычисления  n-точечного  дискретного  преобразования  Фурье  составляет  ,  а  для  вычисления  коэффициентов  модулярного  вейвлет-преобразования  для  количества  отсчетов  сигнала,  равного  n  составит  .  Тогда  значения  выигрыша  по  количеству  операций  для  данных  методов  составит  .

Сравнительные  характеристики  для  обоих  методов  приведены  в  таблице  4.

Таблица  4. 

Сравнение  количества  операций  в  вейвлет-преобразовании  и  преобразовании  Фурье

Таким  образом  применение  вейвлет-преобразования  для  распознавания  речи  позволяет  получить  выигрыш  по  быстродействию  по  сравнению  с  дискретным  преобразованием  Фурье.  Проведенные  исследования  показали,  что  применение  модулярных  преобразований  позволяет  повысить  точность  анализа  речевых  сигналов,  представленных  в  цифровом  виде.

Список  литературы:

1.Рабинер  Л.Р.,  Шафер  Р.В.  Цифровая  обработка  речевых  сигналов.  М.:  Радио  и  связь,  1981.  —  300  с.

2.Воробьев  В.И.,  Грибунин  В.Г.  Теория  и  практика  вейвлет-преобразования.  СПб.  :  ВУС  им.  Буденного,  1999.  —  208  с.

3.Добеши  И.  Десять  лекций  по  вейвлетам.

4.Дьяконов  В.П.  Вейвлеты.  От  теории  к  практике.  М.:  СОЛОН-Р,  2002.  —  446  с.

5.Юрков  П.Ю.,  Федоров  В.М.,  Бабенко  Л.К.  Распознавание  фонем  русского  языка  с  помощью  нейронных  сетей  на  основе  вейвлет-преобразования.  //  Нейрокомпьютеры:  разработка  и  применение,  —  2001.  —  №  7—8,  —  с.  87—93.

6.Червяков  Н.И.,  Ряднов  С.А.,  Сахнюк  П.А.,  Шапошников  А.В.,  Модулярные  параллельные  вычислительные  структуры  нейропроцессорных  систем.  М.:  ФИЗМАТЛИТ,  2003.  —  288  с.

7.Смирнов  В.И.  Курс  высшей  математики.  Том  1.  М.:  Наука,  1967.  —  479  с.

8.Боровков  А.А.  Теория  вероятностей.  Новосибирск:  Издательство  института  математики,  1999.  —  470  с.