РЕШЕНИЕ  ЗАДАЧ  ВИБРОПОЛЗУЧЕСТИ  В  МАТРИЧНОЙ  ФОРМЕ

Слободянюк  Сергей  Александроваич

д-р  техн.  наук,  профессор,  Приднепровская  государственная  академия  строительства  и  архитектуры,  Украина,  г.  Днепропетровск

Буратинский  Андрей  Петрович,

аспирант,  Приднепровская  государственная  академия  строительства  и  архитектуры,  Украина,  г.  Днепропетровск

E-mail:  buric@ua.fm

Существенным  препятствием  в  развитии  теории  расчета  железобетонных  конструкций  на  длительные  нагрузки  является  необходимость  решения  систем  интегральных  или  дифференциальных  уравнений,  порождаемых  условиями  совместности  деформаций.  Как  известно,  решение  системы  интегрально-дифференциальных  уравнений  в  замкнутом  виде  получено  быть  не  может. 

Если  длительные  нагрузки  во  времени  меняются  «медленно»  и  без  учета  сил  инерций,  то  их  относят  к  статическим  нагрузкам.  Такими  задачами  занимается  теория  ползучести  (статическая  ползучесть).  При  длительных  постоянных  нагрузках  решают  задачи  простой  ползучести.

Если  длительные  нагрузки  во  времени  меняются  «быстро»  и  с  учетом  сил  инерций,  то  их  относят  к  динамическим  нагрузкам.  Такими  задачами  занимается  теория  динамической  ползучести.  При  длительных  постоянных  и  высокочастотных  нагрузках  решают  задачи  виброползучести.

В  теории  статической  ползучести  разработан  метод  начальных  параметров  ползучести  проф.  Е.А.  Яценко  [5]  и  модифицированный  метод  начальных  параметров  ползучести  проф.  С.А.  Слободянюка  [3],  которые  позволяют  избежать  необходимости  рассмотрения  интегральных  или  дифференциальных  уравнений  ползучести,  сводя  расчеты  к  матричным  процедурам  и  получают  точные  результаты  при  удержании  не  более  10  членов  ряда.

В  теории  динамической  ползучести  такие  методы  отсутствуют.  Разработаем  аналогичный  метод  для  виброползучести  бетона  на  основе  и  по  методике  [3].

Виброползучесть  —  это  свойства  материала  деформироваться  при  длительном  действии  постоянных  и  высокочастотных  напряжениях  после  завершения  упругого  деформирования  в  момент  приложения  нагрузки.

При  одноосном  напряженном  состоянии  бетонного  элемента  связь  между  деформациями  ε(t)  и  соответствующими  высокочастотными  во  времени  напряжениями  σ(t)  выразим  на  основе  линейного  интегрального  уравнениям  Вольтерра  2-го  рода:

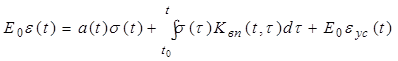,  (1)

где:    —  модуль  упругости  бетона  в  момент  начала  нагружения  при  , 

  —  характеристика  упругих  деформаций; 

  и    —  параметры  изменения  модуля  упругости  во  времени; 

  —  предельная  величина  характеристики  упругих  деформаций.

На  основе  [3,  4]  выразим  интегральное  ядро  виброползучести  через  ядро  ползучести:

,  (2)

где:    —  характеристика  ползучести; 

К_в  —  коэффициент  виброползучести  [1,  4].

В  наследственной  теории  старении  характеристика  ползучести,  предложенная  И.Е.  Прокововичем  и  И.И.  Улицким,  выражается  функцией  [2]:

,  (3)

где:    и    —  предельные  характеристики  обратимых  и  необратимых  деформаций  ползучести  соответственно;  

  и    —  постоянные,  характеризующие  скорость  деформаций  ползучести.

В  ядро  ползучести  (2)  подставим  (3)  и  выполним  преобразования,  получим:

.(4)

Затем  выражение  (4)  подставив  в  (1)  и  после  преобразований  получим: 

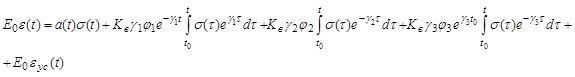.(5)

В  момент  начала  нагружения    и  выражение  (5)  принимает  вид  закона  Гука  для  упругих  деформаций  бетона:

,(6)

где  принято  ;  ;  .

Продифференцируем  выражение  (5)  по  t  и  сгруппируем,  после  чего  получим  следующее  выражение:

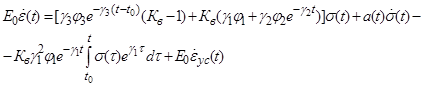,  (7)

где  обозначено  ;  ;  .  При    уравнение  (7)  принимает  вид

.(8)

Продифференцировав  (7)  по  t  второй  раз  и  сгруппировав,  получим:

(9)

После  подстановки  ,получим:

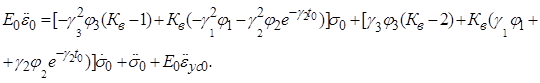  (10)

Дифференцируя  выражение  (9)  и  далее  многократно  по  t  и  после  каждого  дифференцирования  принимая  ,  получим  систему  алгебраических  уравнений,  записанных  здесь  в  свернутой  матричной  форме:

.  (11)

В  (11)  стрелочками  обозначены  бесконечномерные  векторы  начальных  параметров  деформаций  и  напряжений;  Е  —  матричная  единица;  С_вп  —  матрица  влияния  виброползучести.  Вид  указанных  векторов  и  матричной  единицы  следующий:

  (12)

В  векторах  (12)  точками  над  буквами  обозначен  порядок  производной  по  t,  а  нолики  внизу  обозначают,  что  функции  и  их  производные  взяты  при  .

Матрицу  влияния  виброползучести  рационально  выразить  в  виде  суммы  трех  матриц:  обратимых  C_1в,  необратимых  С_2в  и  упругих  C_3в  деформаций:

С_вп=С_1в+С_2в+С_3в,    (13)

значение,  которых  следующее:

Элементы  матриц  (13)  вычисляются  по  рекуррентным  формулам.  При  вычислении  числовых  коэффициентов  элементов  матриц  С_2в  и  C_3в,  укладывающихся  в  схему  ,  применяется  алгоритм  x=a-b.

Дальнейшая  методика  расчета  соответствует  [3].

В  частном  случае,  когда  коэффициент  виброползучести  К_в=1  из  матрицы  влияния  виброползучести  получается  матрица  влияния  ползучести  [3],  то  есть  С_вп=С,  а  С_1в=С₁,  С_2в=С₂,  С_3в=С₃.

Рассмотрим  пример  расчета  МНПВП.  Берем  одноосный  бетонный  элемент  единичной  длины  (рис.1),  на  торцах,  которого  приложено  напряжение  σ(t)=  σ+  Δσ  sinω(t-t₀),  где  =10  МПа  и  =0,5  МПа. 

Рисунок  1.  Нагрузка  на  бетонный  образец

При  учете  только  квазипостоянных  напряжений  во  времени:

.    (14)

В  любой  момент  времени,  начальные  параметры  возбуждающей  функции  будут  иметь  вид:

    (15)

Тогда  разрешающие  уравнение  (11)  в  развернутом  виде  без  учета  усадки  будет  иметь  вид:

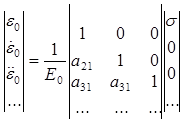.(16)

где  ;  ;  .

Искомую  деформацию  виброползучести  найдем  через  ряд  Тейлора  улучшенной  сходимости  [3]:

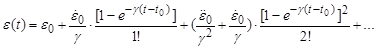                                (17)

Чтобы  получить  точное  уравнение  деформаций  виброползучести  в  общем  виде,  в  (5)  подставим  σ(t)=  σ+  Δσ  sinω(t-t₀)  и  проинтегрируем.  После  преобразований  получим:

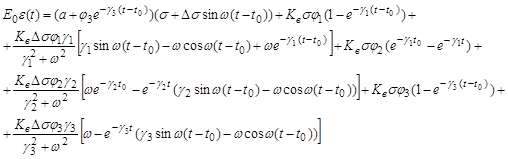.     (18)

Было  получено  точное  интегральное  решение  по  (18)  и  МНПВП  по  (17)  при  следующих  значениях:  К_в=2,  t₀=53  суток;  Е_b=30000  МПа;  f=50  Гц;  27,13  10⁶  1/сут;  φ₁=0,5;  φ₂=1,5;  φ₃=0,2;  a=0,8;  γ₁=γ₂=γ₃=0,004  1/сут.

Результат  точного  решение  и  по  МНПВП  графически  показаны  на  рис.  2.

Рисунок  2.  Нагрузки  (а)  и  деформации  виброползучести  бетонного  образца  (б)

Анализ  результатов  показывает,  что  решение  МНПВП  при  5  членах  ряда  практически  совпадают  с  точным  решение.  Расхождение  на  600  сутках  не  превышает  1  %.

Выводы.  Таким  образом,  разработан  метод  теории  динамической  ползучести  бетона,  названный  методом  начальных  параметров  виброползучести  (МНПВП).  Он  позволяет  решать  различные  граничные  задачи  виброползучести  в  матричной  форме  вплоть  до  получения  начальных  параметров  искомой  функции,  а  определение  искомой  функции  при  любом  времени  можно  производить  с  помощью  ряда  Тейлора  улучшенной  сходимости. 

Список  литературы:

1.Бондаренко  В.М.  Некоторые  вопросы  нелинейной  теории  железобетона.  Х.:  ИХУ,  1968.  —  324  с.

2.Прокопович  И.Е.  Влияние  длительных  процессов  на  напряженное  и  деформированное  состояние  сооружений.  М.:Госстройиздат,  1963.  —  260  с.

3.Слободянюк  С.А.  Модифицированный  метод  начальных  параметров  ползучести  //  Вестник  ПГАСА.  Д.:  ПГАСА,  —  1998.  —  №  3.  —  С.  33—38.

4.Шкарбелис  К.К.  Влияние  вибраций  на  ползучесть  железобетонных  конструкций  //  Сб.  «Вопросы  динамики  и  динамической  прочности».  М.:  Стройиздат,  —  1956.  —  вып.  4.  ––  С.  27—35.

5.Яценко  Е.А.  Метод  начальных  параметров  теории  железобетона//  Исследование  по  механике  строительных  конструкций  и  материалов.  Л.:  ЛИСИ,  1986.  —  C.  66—72.