Статья опубликована в рамках: V Международной научно-практической конференции «Наука вчера, сегодня, завтра» (Россия, г. Новосибирск, 16 октября 2013 г.)
Наука: Сельскохозяйственные науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
АЛГОРИТМИЗАЦИЯ ПРОЦЕССА НАХОЖДЕНИЯ ПАРЕТТО-ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДЛЯ ГРУППЫ МОБИЛЬНЫХ РОБОТОВ
Проталинский Игорь Олегович
Астраханский Государственный Технический Университет, Астрахань
E-mail:
Сегодня все большую область применения в промышленности и бытовой сфере находят мобильные роботы. Однако применение одного мобильного робототехнического комплекса не эффективно. Для решения комплексных задач целесообразно использовать группу мобильных роботов.
Для формирования управляющего воздействия для группы мобильных роботов целесообразно использовать математический аппарат методов многокритериальной оптимизации. Управляющим воздействием группы мобильных роботов будим называть набор стратегий для выполнения множества взаимосвязанных задач с максимальной эффективностью
Для решения задачи поиска наиболее эффективного набора стратегий стратегии необходимо произвести анализ методов многокритериальной оптимизации: метод весовых коэффициентов, метод эпсилон-ограничений, метод последовательных уступок и метод справедливых компромиссов. Проанализируем представленные методы по следующим параметрам: использование относительной важности критериев, сводимости к однокритериальной задаче, необходимости нормализации критериев и обязательная упорядоченность критериев.
Метод весовых коэффициентов позволяет свести задачу многокритериальной оптимизации к задаче однокритериальной оптимизации [1] и основан на назначении каждому частному критерию весового коэффициента, определяющего его относительную важность. Все критерии, умноженные на свои весовые коэффициенты, складывают, образуя единый скалярный критерий оптимальности, по которому производят дальнейшую оптимизацию. Перед выбором весовых коэффициентов выполняется нормализация частных критериев, чтобы их задачи были сопоставимы [2]. Недостатком данного метода является необходимость использования экспертной оценки в процессе распределения весов [3].
Метод эпсилон-ограничений позволяет свести многокритериальную задачу к задаче однокритериальной оптимизации, и основан на выделении наиболее важного частного критерия, по которому в последующем производится дальнейшая оптимизация, при ограничении остальных критериев неизменяемыми значениями. Для использования данного метода необходима информация о значении констант, которые используются для ограничения критериев. Основными недостатками метода является сложность выбора максимального допустимых значений частных критериев и жесткость ограничений [4].
Метод последовательных уступок основан на расположении частных критериев в порядке убывания их важности и назначении уступок (т. е. максимальных отклонений от оптимального значения), допустимых для каждого критерия. Метод позволяет контролировать, какой ценой уступки одного частного критерия приобретается выигрыш в другом частном критерии. Метод применяется только для решения класса задач оптимизации, в которых частные критерии упорядочены по степени важности [5].
Метод справедливых компромиссов основан на последовательном итерационном поиске компромиссного решения, при котором относительный уровень снижения выигрыша одного или нескольких частных критериев не превосходит относительного уровня повышения выигрыша остальных частных критериев.
На основе проведенного анализа для решения задачи группового управления роботами наиболее подходящим методом многокритериальной оптимизации является метод справедливого компромисса.
Цель работы: синтезировать алгоритм поиска паретто-оптимальной стратегии группы мобильных роботов на основе метода справедливых компромиссов, для нахождения наиболее эффективного управляющего воздействия.
При решении задачи управления группой роботов {R} классический подход решения методом справедливых компромиссов малоэффективен вследствие: большого количества роботов N в группе {R} и взаимосвязей между задачами внутри множества {Z}, поэтому возможно появление случаев, когда при поиске паретто-оптимального множества стратегий {![]() } наиболее эффективной стратегией для группы {R} является стратегия с не максимальным значением суммарной выигрыша
} наиболее эффективной стратегией для группы {R} является стратегия с не максимальным значением суммарной выигрыша ![]() при выполнении стратегии. Таким образом, необходимо произвести корректировку метода для решения задачи управления группой мобильных роботов. Решением является изменение условий поиска значения коэффициентов
при выполнении стратегии. Таким образом, необходимо произвести корректировку метода для решения задачи управления группой мобильных роботов. Решением является изменение условий поиска значения коэффициентов ![]() и
и ![]() .
.
Вычислим суммарное снижение мощности для группы роботов при переходе от множества стратегий ![]() к
к ![]() :
:
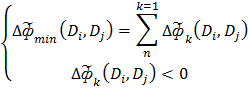 (1)
(1)
где: n — количество роботов в группе {R}.
Аналогично вычисляем повышения мощности для группы роботов при переходе от множества стратегий ![]() к
к ![]() :
:
 (2)
(2)
Будем говорить, что множество стратегий для группы роботов ![]() эффективнее множества
эффективнее множества ![]() , если выполняется условие:
, если выполняется условие:
![]() (3)
(3)
Таким образом, при выполнении условия (3), происходит переход от выполнения группой роботов {R} множества стратегий ![]() к выполнению множества стратегий
к выполнению множества стратегий ![]() .
.
Аналогично будем говорить, что множество стратегий для группы роботов ![]() эффективнее множества
эффективнее множества ![]() , если выполняется условие
, если выполняется условие
![]() (4)
(4)
При выполнении условия (4) не происходит перехода от выполнения группой роботов {R} множества стратегий ![]() к выполнению множества стратегий
к выполнению множества стратегий ![]() .
.
Таким образом, паретто-оптимальным множеством стратегий {![]() } называется такое множество, которое всегда выполняет условие 4 (рис. 1).
} называется такое множество, которое всегда выполняет условие 4 (рис. 1).
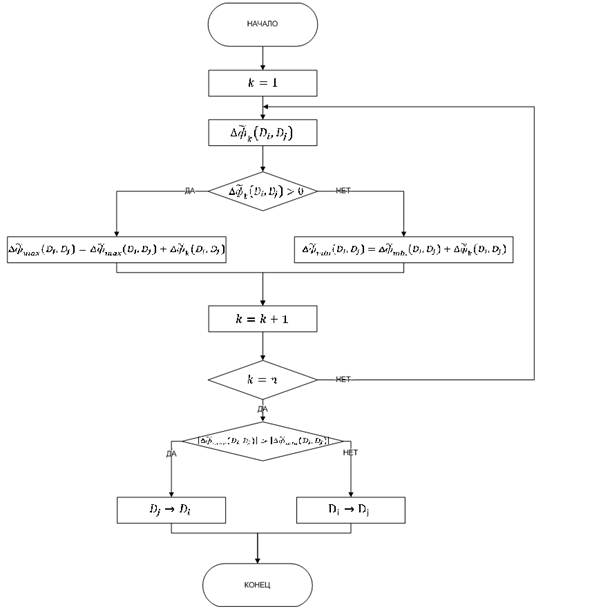
Рисунок 1 Алгоритм поиска оптимального множества методом справедливых компромиссов
Рассмотрим метод справедливых компромиссов для нахождения оптимального множества стратегий {![]() } группы роботов {R} для решения множества взаимосвязанных задач {Z}, как алгоритм выполнения вычислительной системой i-ым роботом, где критерием оптимальности является
} группы роботов {R} для решения множества взаимосвязанных задач {Z}, как алгоритм выполнения вычислительной системой i-ым роботом, где критерием оптимальности является ![]() — суммарная мощность стратегии
— суммарная мощность стратегии ![]() . Таким образом, входными данными алгоритма справедливых компромиссов (рисунок 1) являются два альтернативных множества стратегий {
. Таким образом, входными данными алгоритма справедливых компромиссов (рисунок 1) являются два альтернативных множества стратегий {![]() } и {
} и {![]() }, а результатом работы алгоритма: выбор стратегии, обладающей большим значением показателя критерия оптимальности. Решение представляет собой циклический алгоритм с ветвлением.
}, а результатом работы алгоритма: выбор стратегии, обладающей большим значением показателя критерия оптимальности. Решение представляет собой циклический алгоритм с ветвлением.
Использование синтезированного алгоритма поиска управляющего воздействия группы мобильных роботов на основе метода справедливых компромиссов позволит повысить эффективность работы группы роботов при решении задач картографического исследования территорий, охраны и патрулирования.
Список литературы:
1.Захаров И.Г. Обоснование выбора. Теория практики. СПб: Судостроение, 2006.
2.Ларичев О.И. теория и методы принятия решений М.: Логос, 2000
3.Лотов А.В., Бушенков А.В., Каменев А.В., Черных О.Л. Компьютер и поиск компромисса. Метод достижимых целей. М.: Наука, 1997
4.Москвин Д.А., Калинин М.О. Перспективы использования многокритериальной оптимизации при управлении безопасностью информационных систем Т.: Доклады ТУСУРа, № 2 (18), часть 1, 2008
5.Штойер Р. Многокритериальная оптимизация: теория, вычисления и приложения М.: Радио и связь, 1992
6.Protalinskii I.O., Sherbatov I.A., Shishkin N.D. Optimal Strategy Synthesis for a Group of Mobile Robots with Variable Structure// World Applied Sciences Journal 24 (Information Technologies in Modern Industry, Education & Society): 268-275, 2013
дипломов


Оставить комментарий