ЭЛЕКТРОСТАТИЧЕСКАЯ  СИСТЕМА  КОНТАКТА  ШОТТКИ  (3D-МОДЕЛИРОВАНИЕ)

Купрейчик  Антон  Федорович

магистрант,  Томский  государственный  университет  систем  управления  и  радиоэлектроники,  Томск,  ОАО  Научно-исследовательский  институт  полупроводниковых  приборов,  Томск

E-mail: 

Бабак  Леонид  Иванович

д-р  техн.  наук,  профессор,  Томский  государственный  университет  систем  управления  и  радиоэлектроники,  Томск

Минин  Олег  Николаевич

магистрант,  Томский  государственный  университет  систем  управления  и  радиоэлектроники,  Томск,  ОАО  Научно-исследовательский  институт  полупроводниковых  приборов,  Томск

Новиков  Вадим  Александрович

канд.  физ.-мат.  наук,  старший  научный  сотрудник  НОЦ  Наноэлектроника  Томского  государственный  университета,  Томск

Сальников  Андрей  Сергеевич

аспирант,  Томский  государственный  университет  систем  управления  и  радиоэлектроники,  Томск

Торхов  Николай  Анатольевич

канд.  физ.-мат.  наук,  ОАО  Научно-исследовательский  институт  полупроводниковых  приборов,  Начальник  технической  лаборатории  отдела  4,  Томск

Введение

Контакты  металл-полупроводник  (М-П)  с  барьером  Шоттки  (БШ)  широко  используются  для  выпрямления  тока,  в  качестве  одного  из  основных  элементов  ряда  полупроводниковых  СВЧ-устройств,  а  также  для  исследования  фундаментальных  физических  параметров  полупроводниковых  материалов.  Такие  контакты  используются  как  затворы  в  полевых  транзисторах,  в  качестве  стока  и  истока  в  МОП-транзисторах,  электродов  в  мощных  ЛПД-генераторах  [1].  Широкий  круг  использования  выпрямляющих  контактов  М-П  определяет  актуальность  их  использования.

Было  экспериментально  показано  [2—4],  что  величина  электрического  поля  E_l  периферии  l  и  поверхностный  потенциал  (ПП)  j_m,contact  =  j_m,contact  (P)  (работа  выхода  электронов)  зависят  от  линейного  размера  (диаметр  D,  или  периметр  P)  контактов  М-П  с  БШ  и  могут  распространяться  за  пределы  контакта  на  расстояния  l  до  35—40  мкм,  что  до  сих  пор  не  находило  достаточного  теоретического  объяснения.  К  примеру,  размер  области  пространственного  заряда  (ОПЗ)  реальных  контактов  обычно  составляет  0,1—0,3  мкм.  Величина  ПП  j_S(m)  исследуемой  поверхности  полупроводника  (S)  или  металлического  контакта  (m)  может  быть  определена  методами  атомно-силовой  микроскопии  (АСМ)  из  выражения:

Δφ_S(m)  =  φ_p  –  φ_S(m)               (1)

где:  Dj_S(m)  —  измеряемая  АСМ-методом  контактная  разность  потенциалов  (КРП), 

j_p  —  ПП  (работа  выхода)  Au-покрытия  иглы  кантилевера.

Как  показали  эксперименты,  уменьшение  D  приводит  к  уменьшению  l  и  увеличению  ПП  металлического  контакта  Шоттки  j_m,contact.  Экспериментально  изменение  j_m,contact  может  быть  определено  из  выражения

φ^*  =  φ_m,film  –  φ_m,contact  (P)  (2)

По  разности  ПП  металлического  контакта  j_m,contact  и  сплошной  металлической  пленки  j_m,film.  Величина  j^*  может  достигать  довольно  больших  значений  0,4—0,6  эВ  [2—4].  Согласно  описанной  в  [2—4]  электростатической  модели  контакта,  электрическое  поле  периферии  E_l  на  расстоянии  Dx  от  контакта  образовано  суперпозицией  электрического  поля  градиента  потенциала  E_grad  и  электрического  поля  E^*  ОПЗ  (рис.  1). 

E_l  =  E_grad  –  E^*                          (3)

В  [2—4]  предполагалось,  что  E_grad  постоянно  и  определяется  только  природой  металла  и  полупроводника,  а  E*  определяется  электрическим  зарядом  ОПЗ  и  поэтому  зависит  от  линейных  размеров  контакта.

В  связи  с  этим  в  настоящей  работе  методами  компьютерного  моделирования  исследуется  влияние  составляющей  E^*  электрического  поля  периферии  E_l  на  электростатическую  систему  круглых  Au-контактов  М-П  с  БШ.

Основная  часть

В  работе  исследовались  золотые  сэндвич  Au-контакты  М-П  с  БШ  диаметром  D  =  5  мкм  и  толщиной  0,1  мкм,  сформированные  на  поверхности  эпитаксиального  слоя  n-n⁺  GaAs(100)  чипа  20´20  мкм  (рис.  2а).  Концентрация  легирующей  примеси  в  эпитаксиальном  слое  n-GaAs  толщиной  0,6  мкм  составляла  N_D(Sn)=6×10¹⁶  см^-3,  а  в  слое  n⁺-GaAs  -  N_D(Sn)=2×10¹⁸  см^-3  и  1  мкм  соответственно.  Омический  контакт  к  чипу  формировался  со  стороны  n⁺-слоя.  Моделирование  электростатической  системы  чипа  с  Au-контактом  Шоттки  в  вакууме  осуществлялось  с  использованием  программного  пакета  Sentaurus  TCAD  Synopsys.  Шаг  сетки  разбиений  выбирался  равным  100  нм,  количество  точек  —  189411.

Рисунок  1.  Периферия  контакта  Шоттки

В  качестве  граничных  выбирались  нулевые  условия  на  сторонах  параллелепипеда,  включающего  моделируемый  чип.  Изгиб  зон  на  поверхности  слоя  n-GaAs  составлял  0.65  эВ,  высота  БШ  j_b=0,9  эВ.  Влияние  составляющей  E_grad  не  учитывалось. 

Трехмерное  моделирование  распределения  E^*  показало,  что  вокруг  контакта  на  поверхности  полупроводника  существует  протяженная  (l>2,5  мкм)  область  пространственного  заряда  (рис.  2b,  Electrostatic  Potential).  Данный  пространственный  заряд  изменяет  электрический  потенциал  пространства  вокруг  Au-контакта  на  достаточно  большом  расстоянии  (l>2,5  мкм),  которое  значительно  превышает  протяженность  ОПЗ  (~0,15  мкм).  При  этом  в  области  контакта  потенциал  имеет  минимальное  (в  данном  случае  отрицательное)  значение,  которое  резко  увеличивается  (и  даже  меняет  знак)  при  приближении  к  периферии  (краю  контакта)  и  выходит  на  насыщение  до  значений  Dj_S  при  удалении  за  периметр  контакта  на  расстояние  превышающее  l.  Как  видно  из  поперечного  сечения  А-А  (рис.  2b),  размер  l  практически  не  зависит  от  расстояния  до  поверхности  h_Z.  Из  профиля  поперечного  сечения  Dj(Y)  (рис.  2с)  видно,  что  модельное  значение  l  с  достаточной  точностью  совпадает  с  экспериментальным  значением  2,5—3  мкм.  При  этом  увеличение  h_Z  приводит  к  заметному  размытию  (уширению)  переходной  области  потенциала,  расположенной  в  области  периферии  контакта.

В  то  же  время,  как  показало  моделирование,  увеличение  D  приводит  к  увеличению  l  от  2,5  мкм  для  D  =  5  мкм  до  8—10  мкм  для  D  =  200  мкм,  что  определяется,  по  всей  вероятности,  распределением  электрического  заряда  вокруг  контакта  под  действием  составляющей  E*  электрического  поля  периферии  E_l.  Это  подтверждает  сделанное  ранее  (см.  [1]  и  рис.  1)  предположение  о  значительном  влиянии  составляющей  E*  на  электрическое  поле  периферии  выпрямляющих  контактов  М-П.  Моделирование  показало,  что  в  данном  случае  величина  Dj_m  не  зависит  от  диаметра  контакта  и  для  D  =  5  мкм  меньше  экспериментального  значения  на  ~0,46  эВ.  Данный  факт  указывает  на  то,  что  наблюдаемое  на  практике  изменение  Dj_m  при  вариации  линейного  размера  контакта  D  не  связано  с  составляющей  E^*.  Для  определения  влияния  составляющей  E_grad  электрического  поля  периферии  E_l  необходимо  проведение  дальнейших  исследований.

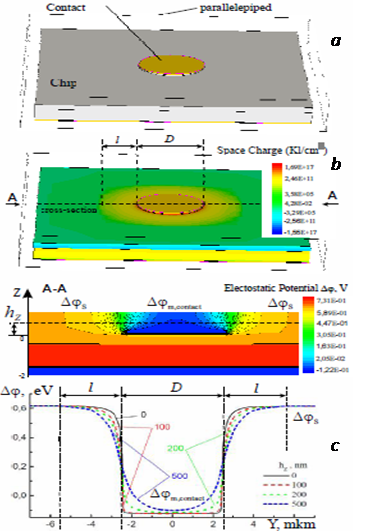
Рисунок  2.  Конструкция  контакта  D=5  мкм  —  а),  плотность  электрического  заряда  —  b),  сечение  A-A  и  профиль  Dj(y)  в  зависимости  от  расстояния  до  поверхности  h_Z  —  с)

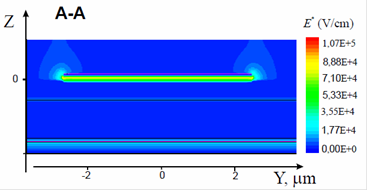
Рисунок  3.  Распределение  электрического  поля  E^*  в  контакте  М-П  с  БШ

Заключение

Трехмерное  моделирование  электростатической  системы  контакта  М-П  с  БШ  подтвердило  наличие  наблюдаемых  вокруг  контактов  протяженных  ореолов  с  пониженной  КРП.  Согласно  полученным  результатам,  изменения  поверхностных  потенциалов  вокруг  контактов  вызваны  распространением  на  достаточно  большие  (в  данном  случае  l»2,5  мкм)  расстояния  электрического  заряда  ОПЗ  под  действием  составляющей  E^*  электрического  поля  периферии  E_l.  Было  найдено,  что  составляющая  E^*  приводит  к  увеличению  l  при  увеличении  диаметра  и  при  этом  практически  не  влияет  на  изменение  поверхностного  потенциала  в  области  контакта  Dj_m,  наблюдаемое  на  практике  при  изменении  его  диаметра  D. 

Проведение  данных  исследований  в  дальнейшем  помогут  в  полной  мере  учесть  влияние  периферийного  электрического  поля  на  характеристики  полупроводниковых  приборов,  где  используется  контакт  М-П  с  БШ.

Список  литературы:

1.Зи  C.  Физика  полупроводниковых  приборов:  В  2-х  книгах.  Кн.  1.  Пер.  с  англ.  —  2-е  перераб.  и  доп.  изд.  М.:  Мир,  1984.  —  456  с.

2.Торхов  Н.A.  Поверхностный  потенциал  контактов  металл-полупроводник  с  барьером  Шоттки.  Изв  ВУЗов  Физика  Деп  в  ВИНИТИ  №  334-В2008  от  18.04.2008.

3.Torkhov  N.A.  “Effect  of  the  Periphery  of  Metal–Semiconductor  Contacts  with  Schottky  Barriers  on  their  Static  Current–Voltage  Characteristic”,  Semiconductors,  44(5),  1—12  (2010).

4.Torkhov  N.A.  “The  Nature  of  Electrical  Interaction  of  Schottky  Contacts”,  Semiconductors,  45(8),  1009—1025.  (2011).