ВОПРОСЫ  ИСПОЛЬЗОВАНИЯ  ПАРАМЕТРИЧЕСКИХ  МОДЕЛЕЙ  ПРИ  ПРОЕКТИРОВАНИИ  АВИАЦИОННЫХ  КОНСТРУКЦИЙ

Ерохин  Александр  Павлович

аспирант  Московского  авиационного  института  (национального  исследовательского  университета),  г.  Москва

E-mail: 

В  настоящее  время  проектирование  с  использованием  параметрических  геометрических  моделей  считается  основным  методом  повышения  эффективности  автоматизированного  проектирования  машиностроительных  изделий.  Вопросами  применения  параметрических  моделей  как  метода  повышения  эффективности  проектирования  занимались  В.Н.  Малюх,  И.П.  Норенков,  Б.С.  Воскобойников,  В.Л.  Митрович,  В.П.  Иванов,  А.С.  Батраков,  С.В.  Матвеев,  А.Т.  Фоменко,  C.  Matthews,  S.A.  Meguid,  J.  Lee,  B.  Uyer,  E.  Endgel,  G.  Snouke  [1,  с.  8].

Однако,  в  настоящее  время  окончательно  не  решена  проблема  использования  параметрических  геометрических  моделей  на  стадии  рабочего  проектирования  авиационных  конструкций.  В  частности,  особый  интерес  представляет  параметризация  геометрических  моделей  деталей,  содержащих  криволинейные  поверхности  теоретического  контура  (ТК)  летательного  аппарата  (ЛА). 

Построение  электронной  модели  каждой  такой  детали  в  системе  геометрического  моделирования  (СГМ)  само  по  себе  трудоемко  ввиду  сложности  ее  формы.  Помимо  этого,  в  одном  агрегате  могут  присутствовать  многочисленные  группы  деталей  рассматриваемого  типа,  имеющих  между  собой  значительную  степень  конструктивного  и  геометрического  подобия  (например,  стрингера,  пояса  нервюр  и  т.  п.).

Параметрическая  модель  одной  из  группы  таких  деталей  позволила  бы  получить  модели  остальных  деталей  простым  изменением  значения  требуемых  параметров.  Это  снизит  трудоемкость  построения  электронных  моделей  всех  деталей  данной  группы  прямо  пропорционально  числу  входящих  в  группу  деталей.

Современные  СГМ  предоставляют  широкие  возможности  параметризации  моделей,  однако  их  реализации  применительно  к  моделям  деталей,  имеющих  выход  на  ТК,  препятствует  существенная  методическая  проблема.

Рисунок  1.  Группа  геометрически  подобных  фитингов  стыковки  стрингеров  с  бортовой  нервюрой

Построение  группы  моделей  связано  с  изменением  значений  параметров  и  положения  исходной  модели  в  пространстве.  При  изменении  положения  модели  в  пространстве  в  соответствии  с  ТК  и  параметризации  требуется  обеспечить  сохранение  геометрических  построений.

В  статье  рассматриваются  общие  подходы  к  мультипликации  по  теоретическому  контуру  параметрических  моделей  авиационных  конструкций. 

Отмечается,  что  при  выполнении  электронных  моделей  деталей  (ЭМД)  авиационных  конструкций,  в  качестве  вспомогательной  геометрии  используется  т.  н.  электронная  мастер-геометрия  соответствующих  частей  изделия.

Электронная  мастер-геометрия  изделия  (ЭМГ)  содержит  все  данные,  определяющие  размеры,  форму,  конструктивно-силовую  схему,  взаимное  расположение  составных  частей  изделия,  схему  конструктивно-технологического  членения,  трассировку  систем  управления  и  коммуникаций.  В  частности  в  состав  ЭМГ  входят:

·     базовые  и  строительные  плоскости  ЛА  и  его  главных  составных  частей;

·     поверхности  ТК;

·     базовые  и  строительные  плоскости  и  оси  силового  набора  (нервюр,  лонжеронов  стрингеров  и  т.  п.).

Вводится  понятие  «привязка».  Привязкой  называется  геометрический  элемент  вспомогательной  геометрии,  служащий  размерной  базой  для  геометрической  модели  детали.  Для  рассматриваемого  класса  деталей  привязками  будут  в  первую  очередь  оси  силового  набора  и  поверхности  ТК.  Определение  привязок  при  выполнении  электронной  модели  производится  путем  импорта  соответствующих  геометрических  элементов  из  ЭМГ  в  ЭМД.

Таким  образом,  построение  модели  начинается  с  определения  привязок.  Мультипликация  моделей  осуществляется  между  осевыми  плоскостями  и  поверхностями  конструктивно-силовой  схемы  (КСС)  крыла,  расположенными  в  пространстве  дискретно.  То  есть  при  мультипликации  требуется  изменение  части  привязок. 

Показано,  что  причина  сбоев  перестроения  геометрии  заключается  в  замене  привязок.  Следовательно,  требуется  найти  способ  избежать  замены  их  при  изменении  положения  модели  в  конструкции.

Отмечается  следующая  закономерность  задания  осей  КСС:  дискретно  расположенные  в  пространстве  оси  силового  набора  задаются  параллельным  смещением  с  определённым  шагом  плоскостей  от  некоторой  исходной  плоскости.

Эта  закономерность  позволяет  перейти  от  дискретного  к  непрерывному  способу  определения  осевых  элементов,  используемых  в  качестве  привязок.  Для  этого  предлагается  использовать  в  качестве  привязок  не  сами  оси  силового  набора,  а  элементы,  служащие  для  них  размерными  базами.  В  этой  связи  вводится  термин  «базовые  привязки».

Тогда  привязки  модели  можно  получать  построением  внутри  модели  на  основе  имеющихся  базовых  привязок,  а  не  импортировать  из  мастер-геометрии.  Такая  схема  определения  привязок  позволит  обойтись  без  их  замены  при  изменении  положения  модели.  Достаточно  будет  изменить  численное  значение  параметра,  определяющего  положение  привязки  относительно  базовой  привязки. 

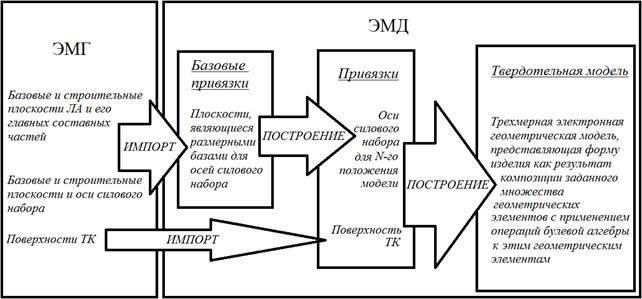
Рисунок  2.  Разработанная  схема  определения  привязок

Разработанная  схема  определения  привязок  модели  позволит  избежать  сбоев  перестроения  геометрических  элементов  при  изменении  положения  модели  в  конструкции  агрегата.  Кроме  этого  она  позволит  получить  модель,  у  которой  параметризуется  не  только  форма,  но  и  положение  в  пространстве. 

Таким  образом,  на  основе  данной  схемы  возможна  разработка  методики  построения  параметрических  моделей  авиационных  конструкций  с  учетом  мультипликации  по  теоретическому  контуру.  Ожидается,  что  такая  методика  позволит  устранить  вышеописанные  трудности  построения  параметрических  моделей.  Разработка  такой  методики  позволит  снизить  трудоемкость  построения  электронных  моделей  групп  геометрически  подобных  деталей  прямо  пропорционально  числу  деталей  в  группе.

Список  литературы:

1.Кандаулов  В.М.  Проектирование  семейств  сложных  машиностроительных  изделий  на  основе  паттернов  —  дисс.  ...  канд.  техн.  наук:  05.13.12  /  В.М.  Кандаулов.  Ульян.  гос.  техн.  ун-т,  Ульяновск,  2012,  —  192  с.  ил.