СОЗДАНИЕ  ПРОМЫШЛЕННОЙ  САР  ПОД  КЛЮЧ

Фитерман  Михаил  Яковлевич

канд.  техн.  наук,  доцент  национального  минерально-сырьевого  университета  «Горный»,  г.  Санкт-Петербург

E-mail:  mfiterman@bk.ru

Введение.

Сегодня  главная  проблема  создания  промышленной  САР  —  это  не  теоретические  или  технические  трудности  ее  синтеза,  проектирования  и  внедрения.  Эти  задачи  давно  решены  и  стандартизированы.  Еще  не  решенной  проблемой  является  настройка  системы  в  условиях  ее  нормального  функционирования,  т.  е.  без  отключения  регулятора.  Специальный  анализ  работы  350  промышленных  предприятий  по  всему  миру,  проведенный  известной  фирмой  Honeywell,  показал,  что  значительная  часть  систем  регулирования  (около  75  %)  настроены  плохо  и  это  обуславливает  заметный  технологический  и  экономический  ущерб  предприятия  [1].  Причиной  такого  положения  является  слишком  редкая  перенастройка  систем  регулирования  ввиду  недостаточности  человеческих  ресурсов  для  такой  деятельности.  На  заводах  на  одного  специалиста  автоматчика  сегодня  приходятся  десятки  и  сотни  локальных  контуров  стабилизации  технологических  параметров  и  все  их  настраивать  и  перенастраивать  ему  некогда.  Существующие  же  на  сегодня  приемы  и  устройства  не  позволяют  полностью  автоматизировать  эту  деятельность.  Как  известно,  для  настройки  коэффициентов  регулятора  необходимо  возбуждать  объект  регулирования,  анализировать  реакцию  его  выхода  на  эти  возбуждающие  воздействия  и  в  зависимости  от  этого  изменять  настроечные  константы  (настройки)  регулятора  в  нужную  сторону  до  достижения  оптимального  качества  стабилизации.  Для  такой  настройки  контура  регулирования  обычно  применяют  специальные  возмущающие  воздействия  на  объект:  скачки,  импульсы  или  гармонические  колебания.  Естественно  при  этом  нежелательно  выключать  регулятор  (разрывать  цепь  обратной  связи),  так  как  настройка  контура  регулирования  —  это  протяженная  во  времени  процедура,  в  течение  которой  состояние  объекта  не  стабилизируется.  Особенно  это  критично  для  нестационарных  объектов,  когда  необходима  достаточно  частая  (регулярная)  настройка  данной  системы.  Это  и  порождает  указанный  выше  ущерб  предприятия  от  плохо  настроенных  стабилизирующих  систем.  В  принципе  можно  настраивать  регулятор  без  применения  специальных  воздействий,  анализируя  реакцию  объекта  на  естественные  случайные  возмущения.  При  этом  указанный  ущерб  исключается.  Но  такая  настройка  системы  требует  весьма  высокой  квалификации  настройщика  и  длительного  времени  настройки  каждого  контура  регулирования.  Таким  образом,  все  равно  все  упирается  в  недостаток  человеческих  ресурсов  и  приводит  к  экономическому  ущербу  промышленных  предприятий.

Как  известно,  есть  еще  один  прием  получения  оптимально  настроенной  стабилизирующей  системы  без  собственно  процедуры  настройки.  Для  этого  необходимо  знать  численные  константы  математической  модели  управляемого  объекта.  Тогда  можно  сформулировать  и  решить  задачу  о  минимуме  ошибки  управляемого  параметра  объекта.  Аналитическое  решение  этой  задачи  дает  оптимальный  закон  управления,  а  его  коэффициенты  получаются  как  функции  констант  модели  объекта.  Казалось  бы,  это  исключает  необходимость  экспериментальной  настройки  регулятора.  Но  для  реализации  такого  подхода  необходимо  знать  константы  модели  объекта.  При  создании  же  конкретной  САР  проектировщику  в  лучшем  случае  известны  уравнения  связи  входных  и  выходных  параметров  объекта  в  общем  виде,  без  численных  значений  констант  в  этих  уравнениях.  Это  потому,  что  модель  любого  технологического  объекта  основывается  на  общих  физических  законах  сохранения  и  передачи  массы  и  энергии.  Конкретные  же  численные  значения  указанных  констант  зависят  от  конструктивных  особенностей  данного  технологического  аппарата  и,  как  правило,  заранее  не  известны.  Чтобы  обойти  эту  трудность  можно  попытаться  идентифицировать  выбранную  модель  объекта  и  найти  ее  константы  [2].  Но  здесь  нас  подстерегает  другая  трудность  —  принципиальная  невозможность  идентификации  объекта,  охваченного  обратной  связью  входа  объекта  с  его  выходом  через  регулятор.  Известно,  что  идентификация  любого  объекта  не  корректна,  если  его  вход  функционально  зависит  от  выхода.  Нам  удалось  решить  эту  теоретическую  проблему.  Оказалось,  что  для  этого  следует  идентифицировать  не  собственно  объект  управления,  а  весь  замкнутый  контур  системы,  как  единое  целое  «объект  +  регулятор».  Такая  идентификация  позволяет  получить  неразделяемые  комбинации  констант  объекта  и  настроечных  констант  регулятора.  Однако  регулярное  повторение  такой  процедуры  позволяет  рекуррентно  получать  константы  собственно  модели  объекта,  а  через  них  –  оптимальные  настройки  регулятора.

Таким  образом,  для  получения  оптимальной  САР  по  предлагаемому  методу  необходимо  одновременно  решать  две  согласованные  задачи: 

·     идентификация  констант  контура  регулирования,  как  единого  целого,  и  рекуррентное  получение  констант  модели,

·     определение  оптимальных  настроек  регулятора  в  задаче  минимизации  ошибки  стабилизации.

В  первой  задаче  следует  на  период  идентификации  зафиксировать  настроечные  константы  регулятора,  полученные  на  предыдущем  цикле  настройки.  Тогда  по  окончанию  очередного  цикла  идентификации  легко  вычислить  неизвестные  константы  объекта  из  найденных  констант  всего  контура  при  известных  константах  регулятора.  После  этого  по  второй  задаче  аналитически  определяются  новые  константы  регулятора.  Получается  рекуррентная  процедура  с  непрерывно  повторяемой  идентификацией,  что,  по  сути,  является  адаптацией  системы  управления.  Такой  подход  к  получению  констант  модели  объекта,  а  по  ним  нахождение  оптимальных  коэффициентов  регулятора  мы  назвали  совмещенным  синтезом  САР.  Ниже  этот  подход  развивается  для  линейных  моделей  объектов  общего  вида,  но  для  простоты  и  наглядности  односвязных  (один  управляемый  технологический  параметр  и  один  управляющий  параметр). 

Синтез  закона  управления.

Остановимся  подробнее  на  второй  из  согласованных  задач  —  задаче  синтеза  оптимального  закона  управления  для  САР. 

Как  известно  типовой  односвязный  объект  в  дискретном  времени  и  в  векторной  форме  описывается  линейным  уравнением  следующего  вида:

  (1)

Здесь  X  —  вектор  координат  состояния  объекта  n-го  порядка;  U  —  вектор  управления  с  производными  до  m-го  порядка,  m≤n;  A  —  n  матрица  динамических  констант  объекта,  B  —  n  матрица  статического  коэффициента  передачи  объекта;  V  —  входное  возмущение;  нижние  индексы  _t  ,  _t+1  —  дискретное  время. 

Здесь  полезно  прояснить,  почему  в  модели  объекта  управления  могут  появляться  производные  от  управляющего  параметра.  Такой  вид  моделей  типичен  в  классической  теории  автоматического  управления  (это  модели  с  дробно-рациональными  передаточными  функциями),  но  физическая  и  технологическая  подоплека  этого  в  теории  практически  не  раскрывается.  Из  промышленной  практики  известна  эффективность  применения  регуляторов  с  интегральной  составляющей  (ПИ-  или  ПИД-  регуляторы).  Наличие  И-  составляющей  регулятора  компенсирует  систематическую  ошибку  системы,  которая  обусловлена  постоянной  или  очень  медленно  меняющейся  составляющей  возмущения  в  объекте  V.  С  другой  стороны,  формула  интегральной  составляющей  регулятора  U=K*∫X  эквивалентна  формуле  dU/dt=K*X  с  производной  от  управления  или  в  дискретном  времени  U_t-U_t-1=K*X_t.  Таким  образом,  в  модели  объекта  (4)  в  векторе  управления  U  появляется  дополнительная  компонента  U_t-U_t-1. 

Далее  следует  сформулировать  критерий  качества  управления.  Качество  управления  исчерпывающе  характеризуется  целевой  функцией  только  для  ближайшего  будущего  момента  времени  t+1.  При  этом  целевая  функция  J  в  общем  виде  представляется  квадратичной  формой  X_t+1^т*Q*X_t+1,  где  Q  —  блочная  и  обычно  диагональная  n  —  мерная  матрица  весов  ошибок  управляемых  координат.  Кроме  этого  в  критерии  обычно  учитывают  ограничение  интенсивности  управляющих  воздействий.  Как  известно,  это  несколько  снижает  возможную  точность  стабилизации  состояния  объекта,  но  зато  увеличивает  запас  устойчивости  САР,  что  важно  при  эксплуатации  ее  в  нестационарных  условиях.  Для  этого  в  критерий  качества  управления  вводят  добавку  в  виде  квадратичной  формы  U_t^т*G*U_t,  где  G  —  матрица  весов  управляющего  воздействия  в  критерии.  Итак,  критерий  оптимальности  управления  J  можно  записать  в  виде:

.(2)

После  подстановки  X_t+1  из  (1)  задача  о  минимуме  критерия  J  по  аргументу  U_t  решается  элементарно  (дифференцированием  по  U_t  и  приравниванием  результата  к  нулю)  и  оптимальное  управление  U^opt_t  оказывается  линейной  функцией  X_t.  При  прогнозе  будущего  возмущения  V_t+1=0,  имеем:

  ,  (3)

Здесь    —  расчетный  постоянный  коэффициент,  определяемый  выбранным  критерием  качества  управления  J.

Настройка  АСУ.

Рассмотрим  теперь  первую  согласованную  задачу  совмещенного  синтеза  —  отыскание  констант  объекта,  необходимых  для  реализации  найденного  закона  управления  (3).  Необходимо  найти  матрицы  модели  объекта  A  и  B.  Как  показано  в  [3,  4],  эта  информация  получается  идентификацией  замкнутого  контура  системы  регулирования.  Следуя  идеологии,  примененной  в  [3],  получим  уравнение  замкнутого  контура.  Так  как  на  этой  стадии  коэффициенты  оптимального  управления  (3)  пока  еще  не  определены,  то  запишем  управление  U  в  неопределенной  форме  с  заменой    на  неизвестную  пока  матрицу  K:  .Тогда  уравнение  замкнутого  контура  примет  вид:

,  ,(4)

Здесь  через    обозначена  матрица  коэффициентов,  отыскиваемых  при  идентификации  этого  уравнения.  Из  уравнения  (4)  видно,  что  идентификацией  невозможно  найти  отдельно  матрицы  A  и  B.  Можно  найти  только  их  комбинацию  в  виде  ∆A.  Для  нахождения  самих  матриц  A  и  B  применим  прием,  использованный  в  [3].  А  именно,  в  течение  данного  q-го  цикла  идентификации  зафиксируем  вектор  констант  регулятора  K,  полученный  на  предыдущем  (q-1)-м  цикле  идентификации.  Тогда  по  обозначению  для  матрицы  ,  получаем  на  текущем  q-м  цикле:

.(5)

Далее  по  определению  для  оптимального  регулятора  имеем: 

.(6)

Описанная  пара  процедур  —  идентификация  контура  управления  и  вычисление  оптимальной  настроечной  константы  регулятора  K  циклично  повторяется.  Показано,  что  если  свойства  объекта  управления,  т.  е.  константы  его  модели  не  изменяются  во  времени,  то  регулятор  оказывается  оптимально  настроенным  уже  после  окончания  первого  цикла.  В  противном  случае  нестационарности  объекта,  описанная  процедура  отслеживает  изменения  его  констант  и,  тем  самым,  САР  стремится  сохранять  достигнутую  оптимальность. 

Однако  здесь  следует  отметить,  что  расчетный  коэффициент  R,  используемый  в  формуле  (6),  в  силу  его  определения  (3)  зависит  от  константы  модели  объекта  B.  Но  из  одного  уравнения  (5)  невозможно  найти  обе  искомые  матрицы  A  и  B.  (Это  следствие  того,  что  идентифицируется  не  собственно  объект,  а  весь  контур  регулирования.)  Выход  из  положения  напрашивается  из  принципа  цикличности  описанных  процедур.  Для  пары  двух  соседних  процедур  идентификации  используются,  вообще  говоря,  различные  коэффициенты  регулятора  K_q-1  и  K_q.  Например,  в  цикле  q=1  имеем  K₀  и  получаем  ∆A₁.  На  этом  цикле  K₀  –  это  начальное  фактическое  значение  настроечной  константы  регулятора,  а  величину  B  выбираем  ориентировочно  по  априорной  информации  (обозначим  его  значение  B₁).  Тогда  на  этом  цикле  находим  A₁  и  K₁.  На  следующем  цикле  q=2  имеем  K₁  и  ∆A₂.  Теперь  имеем  два  матричных  уравнения    и  .  Из  этой  системы  двух  уравнений  находим  обе  неизвестные  A  и  B.  (Естественно  обозначить  их  A₂  и  B₂.)  Для  этого  сначала  исключаем  неизвестную  A₂  путем  вычитания  из  первого  уравнения  второго  и  получаем  одно  уравнение  с  неизвестной  B:  .  Отсюда  находим  матрицу  B₂:

.

По  матрице  B₂  вычисляем  расчетный  коэффициент  R  по  формуле  (3),  а  по  формуле  (6)  находим  оптимальную  константу  регулятора  K₂.  Дальше  на  последующих  циклах  q  все  повторяется  аналогично.

Таким  образом,  в  результате  идентификации  уравнения  замкнутого  контура  системы  одновременно  находятся  константы  объекта  A  и  B  и  оптимальные  настройки  регулятора  K^opt.  Полная  функциональная  схема  САР,  созданной  методом  совмещенного  синтеза,  показана  на  рисунке  1.

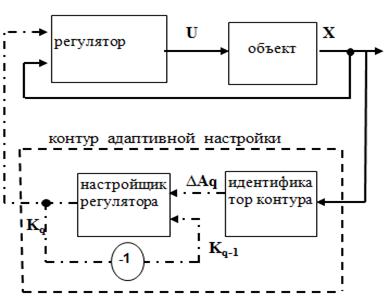
Рисунок  1.  Схема  АСУ,  созданной  методом  совмещенного  синтеза

Идентификатор  и  настройщик  регулятора  образуют  внешнюю  обратную  связь  контура  адаптивной  настройки.  Эта  связь  придает  внешнему  контуру  свойство  астатизма  с  устойчивым  положением  равновесия  в  точке  оптимума  K_q→K^opt.  Это  обстоятельство  и  позволяет  назвать  данную  АСУ  адаптивной. 

Приведенные  схема  и  алгоритм  адаптивной  системы  отвечают  простейшему  варианту  АСУ,  когда  измерительная  информация  о  состоянии  объекта  полная,  а  случайные  возмущения  имеют  характер  белого  шума.  В  случае  не  полной  (но  достаточной)  измерительной  информации,  когда  измеряются  не  все  выходные  параметры  объекта  или  измеряются  с  погрешностью,  в  САР  добавляют  так  называемый  фильтр  оценивания  выходных  параметров.  Это  дополнительный  алгоритмический  блок  после  объекта.  В  случае  возмущений,  сильно  отличающихся  от  белого  шума,  применяют  формирующий  фильтр  возмущений,  формирующий  возмущения  с  заданными  характеристиками  из  белого  шума.  Модель  объекта  вместе  с  моделью  формирующего  фильтра  образует,  так  называемый,  расширенный  объект.  Полезное  свойство  расширенного  объекта  в  том,  что  на  его  входе  действует  возмущение  в  виде  белого  шума.  В  алгоритмах  настройки  САР  при  идентификации  в  условиях  неполной  информации,  вместо  вектора  выхода  X  используются  его  оценки,  получаемые  на  выходе  фильтра  оценивания.  В  этом  случае  для  автонастройки  используются  уже  все  константы  модели:  не  только  константы  регулятора  K,  но  и  константы  объекта  A,  B  (в  алгоритме  фильтра  оценивания).  Заметим,  что  для  САР  без  фильтра  оценивания  можно  упростить  алгоритм  настройщика  регулятора  на  рис.1.  В  этом  случае  следует  идентифицировать  не  уравнение  (4),  а  уравнение,  предварительно  умноженное  слева  на  вектор  R:

(7)

Но  по  определению  R*A  =K,  а  R*B  =γ  —  скалярный  коэффициент,  меньший  0.  Поэтому  данное  уравнение  модели  можно  переписать  в  виде: 

.(8)

Отсюда  видно,  что  в  результате  идентификации  можно  найти  вектор  ∆K_q.  Затем  по  нему  рекуррентно  находится  оптимальный  вектор  констант  регулятора  K_q  по  уравнению:

.(9)

В  качестве  примера  была  проведена  настройка  компьютерного  имитатора  объекта  первого  порядка,  регулируемого  П-регулятором.  На  рисунке  2  приведены  графики  настроечных  констант  этого  регулятора. 

Рисунок  2.  Графики  настроечных  констант  П-регулятора

Нестационарность  данного  объекта  имитировалась  изменением  константы  A  на  интервале  от  30  до  55  циклов  идентификации.  Как  видно  из  графиков  оптимальная  настройка  регулятора  (фактическая  настроечная  константа  регулятора  факт  K  —  черная  линия)  хорошо  отслеживает  идеальную  настройку  в  случае  известной  константы  A  (настроечная  константа  идеал  K  —  красная  линия). 

Заключение.

Процедура  создания  АСР  методом  совмещенного  синтеза  предполагает  следующие  действия  разработчика:

1.  априорный  выбор  порядка  объекта:  значения  величин  n,  m  (это  единственная  необходимая  априорная  информация);

2.  программирование  в  управляющем  устройстве  формул  регулятора  (для  системы  с  не  полной  измерительной  информацией  дополнительно  программирование  формул  фильтра  оценивания);

3.  программирование  алгоритма  идентификатора.

Созданная  таким  образом  АСР  является  адаптивной,  нормально  работает  сразу  после  включения  и  не  требует  дополнительной  настройки.  Это  и  оправдывает  термин  «под  ключ»  в  названии  данной  статьи.  Из  описанной  процедуры  видно,  что  априорная  необходимая  информация  ограничивается  только  порядком  объекта,  т.  е.  порядком  производных  координат  состояния  и  управления,  которые  целесообразно  учитывать  при  управлении  данным  объектом.  Эта  информация  получается  из  опыта  управления  аналогичными  объектами  или  из  результатов  физического  моделирования  этих  объектов  (это  применяется  только  для  достаточно  сложных,  уникальных  объектов).  В  частности,  как  известно  из  промышленной  практики,  в  не  слишком  сложных  задачах  регулирования  достаточно  ограничиться  моделью  объекта  не  выше  третьего  порядка.  Что  касается  порядка  m,  то  можно  рекомендовать  начать  с  m=0.  Это  означает,  что  в  динамической  модели  данного  объекта  не  фигурируют  производные  от  управления.  При  этом  регулятор  вырождается  в  стандартный  П-  или  ПД-  регулятор.  Если  же  предполагается  возможность  заметной  систематической  ошибки  регулирования,  то  следует  выбрать  m=1  или  2.  При  этом  в  законе  управления  возникнет  интегральная  составляющая.  Полученные  результаты  подробно  рассмотрены  для  случая  односвязных  объектов.  Общий  случай  многосвязных  объектов  с  полной  и  тем  более,  не  полной  информацией  будет  рассмотрен  в  следующих  работах.

Полученные  результаты  были  апробированы  на  компьютерном  макете  с  моделями  объектов  разного  вида.  Автор  может  предоставить  эти  результаты  любому  желающему. 

Список  литературы:

1.Перельман  И.И.  Оперативная  идентификация  объектов  управления.  М.  Энергоиздат,  1982.  272  с.

2.Фитерман  М.Я.,  Орищук  А.А..  Настройка  контуров  регулирования  САР  //Промышленные  АСУ  и  контроллеры.  2007,  №  8.

3.Фитерман  М.Я.  Об  информации  и  настройке  в  системах  управления.  //Электронное  издание:  «Сборник  Статей»,  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://d.17-71.com/2007/08/07

4.Штйнберг  Ш.Е.  и  др.  Проблемы  создания  и  эксплуатации  эффективных  систем  пегулирования.  //  Промышленные  АСУ  и  контроллеры.  2006,  №  12.