Разработка конечно-разностного регуляризованного решения одномерной обратной задачи, возникающий в электромагнитных процессах

Маматкасымова Алийма Торожановна

старший преподаватель кафедры «Информатика»

Ошского технологического университета,

Кыргызская Республика, г. Ош

Сатыбаев Абдуганы Джунусович

д-р физ.-мат. наук, проф.,

заведующ ей кафедрой «Управление и информатика в технических системах»

Ошский технологический университет,

Кыргызская Республика, г. Ош

FINITE DIFFERENCE REGULARIZED SOLVE DEVELOPMENT OF ONE-DIMENSIONAL INVERSE PROBLEM ARISING IN ELECTROMAGNETIC PROCESS

Aliyma Mamatkasymova

senior lecturer “Informatics” Osh Technological University,

Kyrgyzstan, Osh

Abdugany Satybaev

dr. Of phys.-maths. sciens., Professor, Head of the Department 
“Management and informatics in technical systems” Osh Technological University,

Kyrgyzstan, Osh

АННОТАЦИЯ

В данной статье построено конечно-разностное регуляризованное решение одномерной обратной задачи уравнения Максвелла.

ABSTRACT

Finite difference regularized solve of one-dimensional inverse problem of Maxwell’s equation had been made in this article.

Ключевые слова: Электромагнитные процессы; уравнения Максвелла; конечно-разностная регуляризация.

Keywords: Electromagnetic processes; Maxwell’s equations; finite difference regularization..

Постановка задачи. Электромагнитные процессы во многих случаях описываются системами уравнений Максвелла.

В работе [1] обратная задача для системы уравнений Максвелла приведена к об- ратной задаче с прямолинейной характеристикой

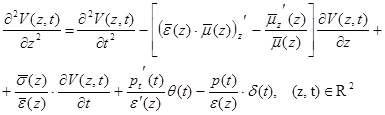         (1)

                                               (2)

Пусть относительно решения прямой задачи задана

                                    (3)

Пусть относительно коэффициентов уравнения выполнены условия

                                              (4)

где:

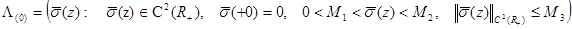
(5)

Тогда, т. к. уравнение (1) является гиперболического типа, задачу можно рассматривать в области [1]:

                                      (6)

Обратная задача. Определить -электропроводимость среды при известных значениях:  -магнитной и диэлектрической проницаемости и p(t) – ток в кабеле, а также дополнительной информации о решении прямой задачи (3).

Обозначим через

.

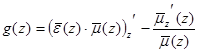Выделим теперь сингулярную и регулярную часть решения прямой задачи (1) – (2) по методике В.Г.Романова, для этого представляем решение задачи в виде [2]:

,                         (7)

где: - гладкая непрерывная функция, θ(t) Хевисайда.

Из (7) получим

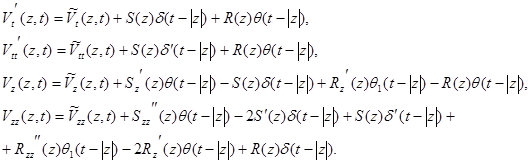
Подставим последние выкладки в уравнение (1), и тогда получим 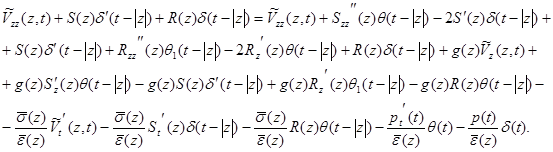 (8)

Собираем коэффициенты при одинаковых  и прирав ниваем их к нулю:

Тогда получим задачи (при этом учтем начальное условие)

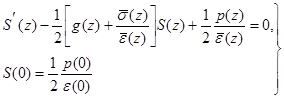(9)

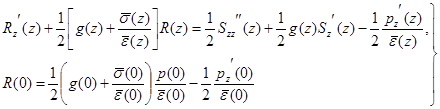(10)

Решая первую систему, получим

 (11)

Решая вторую систему, получим

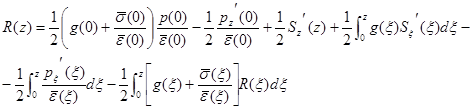(12)

Учитывая, что , а также выше полученных выкладках получим следующую обратную задачу с прямолинейной характеристикой:

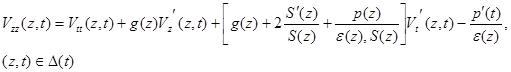(13)

                                                (14)

                                               (15)

Здесь обратная задача заключается в определении функции при известных функциях  (она зависит от известных функций и , при известной функции  – дополнительная информация о решении прямой задачи.

Если мы определим функции , то по формуле

,                          (16)

можем определить и неизвестную функцию .

Используя формулу Даламбера для прямой задачи (13),(14) получим решение этой задачи

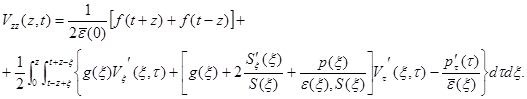(17)

Отсюда, при , то получим

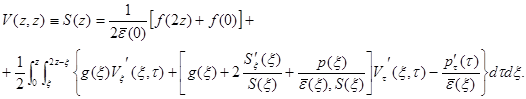.(18)

Конечно-разностное решение. Введем сеточную область для решения задачи (13) – (15)

где: сеточный шаг по

Напишем разностный аналог дифференциального уравнения (13)

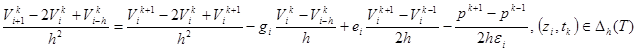.(19)

где:

                                                   (20)

Отюда получим

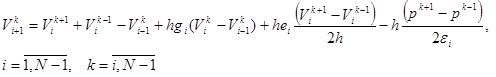(21)

Из последних выражений можно получить рекуретную формулу [3]

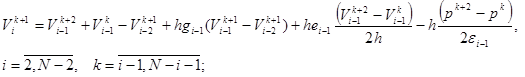
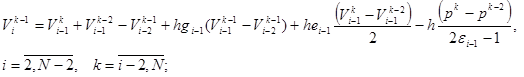
Подставляя последние выражения последовательно в правую часть (21), а также опять же записывая такую же рекуррентную формулу и ее поставляя в (21) и продолжая это процесс получим разностный аналог интегральной формулы Даламбера (17)

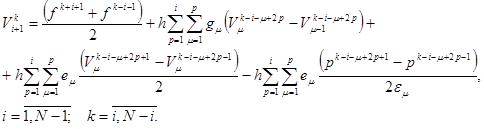(22)

Пологая в последней формуле (22) и учитывая формулы (14), получим разностный аналог интегральной формулы (18)

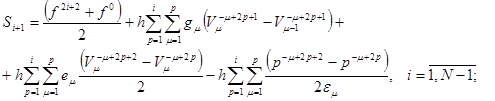.(23)

Таким образом (22) и (23) составляют систему разностных нелинейных уравнений второго рода.

В разностном аналоге (22) мы записали без малых величин .

Таким образом, для формулы (22) с малой величины  можно получить такие же формулы как (22) и (23), но с малой величиной . Обозначим решение с малой величиной  через  и  .

Тогда для  и  получим следующее:

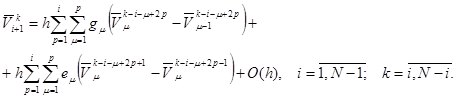(24)

 (25)

Введем обозначения

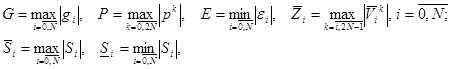(26)

Учитывая эти нормы из (24) и (25) получим оценки

                  (27)

                            (28)

Пусть  тогда

.                                           (29)

Из последней формулы используя формулы дискретнего аналога леммы Гронулла- Беллмана получим

                                                       (30)

Таким образом доказано сходимости конечно-разностного решения разностной задачи (22) (23) к решению дифференциальной задачи (13) – (15).

Теорема 1. Пусть решение обратной дифференциальной задачи (14) (15) суще- ствует и  и тода построенные решения обратной задачи (22) (23) сходится к точному решению  обратной задачи (14) (15) со скоростью порядка .

Регуляризованное решение. Пусть теперь дополнительная информация о решении прямой задачи для решения обратной задачи задана и выполнена

малое число.                         (31)

Тогда для  и  пара регуляризованного решения обратной задачи, также можно получить формулы (22) и (23), т.е.

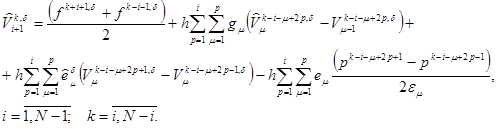(32)

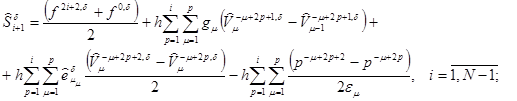(33)

(33) отнимая из формул (22) – (23) формулы (32) – (33) получим

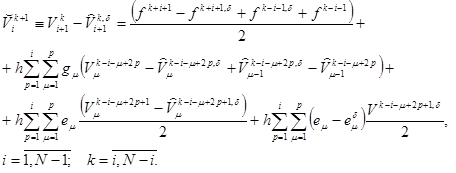(34)

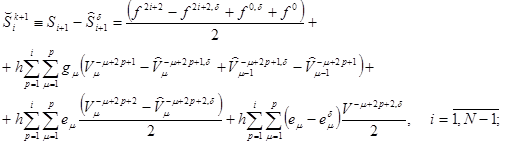(35)

Учитывая введенные нормы оценим последние уравнения (35), (36)

,(36)

.(37)

Пусть теперь  тогда из последних выражений получим

                      (38)

Тогда опять же используя формулы Гроноула-Беллмана получим оценку

,                                           (39)

А если учесть что оценки (30), то имеем

,                                      (40)

Последная оценка является оценкой регуляризующего решения обратной задачи.

Алгоритм конечно-разностного регуляризованного решения.

·     по формуле (15) величинам присваиваются значения  приближенная дополнительная информация обратной задачи (13) – (15) (на рис. 1 обозначена ◦);

·     второму слою  присваиваются значения ( на рис. 1 обозначена ♦). Эта формула выведена из формулы Тейлора;

·     вычисляется формула (14) и определяется значение

·     вычисляется по формуле (14) ;

·     начиная с  слоя, в начале вычисляется , по формуле (32) (на рис.1. обозначена через *);

·     по формуле (33) определяется значение данные на характеристиках;

·     вычисляется интегральное уравнение второго рода, т.е. определяется  по формуле (33);

·     и в каждом слое определяется неизвестная функция , т.е. вычисляется фор- мула (13) и находятся значении .

Функции  были равны к единице. Отметим, что эти функции можно взять как различные тестовые функции. По вышеуказанному алгоритму вычислена обратная задача и она реализована на компьютере с помощью языка Delphi.

Обратная одномерная задача для уравнения Максвелла (13) – (15) численно реализована для функции  в следующего вида и определена функция , глубина вычисления .

В полученных рисунках 2–9 выведены графики функции – дополни тельная информация для обратной задачи  и -точная и приближенная и регуляризованное решение. Шаг сетки .

Таблица 1.

Заданные тестовые функции

Рисунок 1. Область вычисления обратной задачи

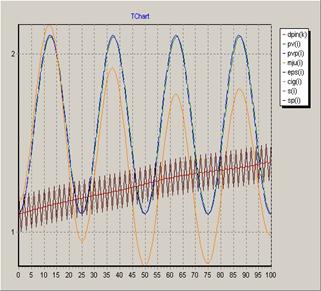
Рисунок 2. График функции

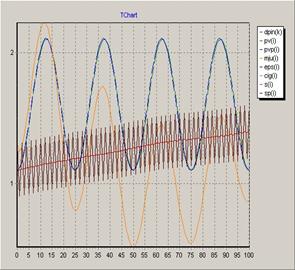
Рисунок 3. График функции

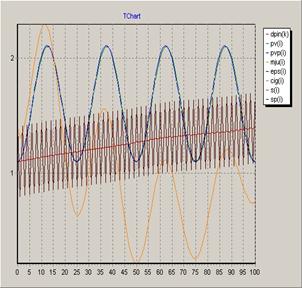
Рисунок 4. График функции

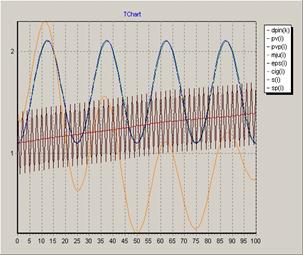
Рисунок 5. График функции  - ступенчатая функция

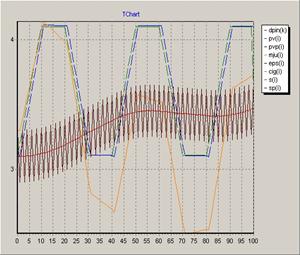
Рисунок 6. График функции  - ступенчатая функция

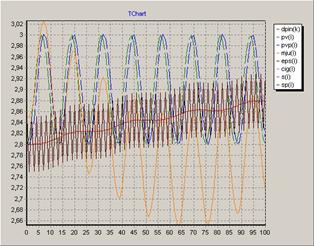
Рисунок 7. График функции

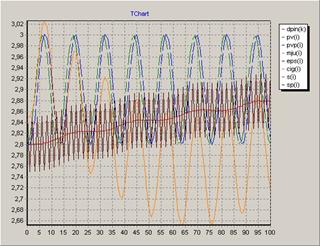
Рисунок 8. График функции  – импульсная  функция;

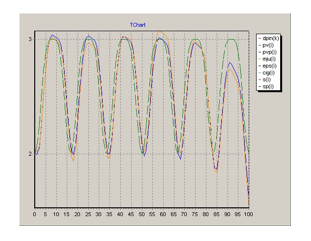
Рисунок 9. График функции

Список литературы:

1. Маматкасымова М.Т., Сатыбаев А.Дж. Численный алгоритм и реализация решения обратной задачи для системы уравнений Максвелла // Проблемы автоматики и управления. ИАИТ НАН КР. – Илим. Бишкек, 2015. С. 208–215.

2. Романов В.Г. Устойчивость в обратных задачах. – М.2005, 296 с.

3. Сатыбаев А.Дж. Конечно-разностное регуляризованное решение обратных задач гиперболического типа. Ош. – Ошоблтипорафия, 2001. – 143 с