ФИЛЬТР  НА  ОСНОВЕ  ФЕРРИТОВОЙ  НЕПЕРИОДИЧЕСКОЙ  СТРУКТУРЫ

Топоркова  Любовь  Владимировна

старший  преподаватель  кафедры  физики 
Поволжского  государственного  университета  телекоммуникации  и  информатики,

РФ,  г.  Самара

E-mail: 

FILTER  BASED  ON  FERRITE  NON-PERIODIC  STRUCTURE

Lubov  Toporkova

senior  lecturer  of  department  of  physics, 
Volga  state  University  of  telecommunications  and  informatics,
Samara

АННОТАЦИЯ

В  данной  работе  рассмотрены  особенности  расчетов  характеристик  фильтров,  на  основе  ферритовой  непериодической  структуры.  Представлены  элементы  матрицы  рассеяния,  позволяющие  рассчитать  коэффициенты  отражения  и  прохождения  для  Е  и  Н-волн.  Данный  метод  расчета  дает  широкие  возможности  использования  его  для  предварительного  численного  моделирования  равномерной  амплитудно-  частотной  характеристики  фильтра,  на  основе  ферритовой  непериодической  структуры.

ABSTRACT

The  work  considers  the  peculiarities  of  characteristics  calculation  for  filters  based  on  non-periodic  ferrite  structures.  It  presents  the  elements  of  the  scattering  matrix  that  allow  calculating  the  reflection  and  transmission  coefficients  for  E  and  H-waves.  This  calculation  method  has  general  applicability  for  preliminary  numerical  simulations  of  the  uniform  amplitude-frequency  characteristics  of  the  filter  based  on  non-periodic  ferrite  structures.

Ключевые  слова:  фильтр;  неппериодическая  ферритовая  структура,  элементы  матрицы  рассеяния.

Keywords:  filters;  non-periodic  ferrite  structures;  elements  of  the  scattering  matrix.

Расчет  характеристик  оптических  фильтров  является  важным  направлением  в  оптоэлектронике.  В  технике  оптической  связи  наиболее  распространены  фильтры  на  основе  брегговских  решеток,  пленочные  фильтры,  также  фильтры  на  основе  дифракционных  решеток.  Фильтры  на  основе  многослойных  пленочных  структур  в  основном  используются  для  мультиплексирования  по  длине  волны,  т.к.  они  позволяют  получить  достаточно  равномерную  амплитудно-  частотную  характеристику  в  области  пропускания.  Для  их  реализации  требуются  прозрачные  оптические  пленки  с  различными  коэффициентами  преломления  и  минимальным  коэффициентом  поглощения  в  требуемой  области  спектра.  Возможность  учитывать  изменение  толщины  слоя  и  значения  углов  подмагничивания  является  дополнительной  степенью  свободы  при  проектировании  оптических  фильтров.

В  данной  работе  рассмотрено  распространение  электромагнитных  волн  в  многослойной  ферритовой  непериодической  структуре  с  толщинами  .  Структура  занимает  область  пространства  ,  где  N-  число  слоев  структуры.  Используя  граничные  условия  [1],  рассмотрим  прохождение  электромагнитной  волны  через  многослойную  структуру,  состоящую  из  тонких  ферритовых  пленок,  различной  толщины.  Каждый  слой  имеет  фиксированную  ориентацию  осей  гиротропии,  определяемых  углами  .  Для  многослойной  структуры  с  анизотропным  параметрами,  описываемыми  матрицами    и  имеющими  толщины    двухсторонние  граничные  условия  могут  быть  представлены  в  виде

  (1)

где  произведение  матриц  в  фигурных  скобках  нельзя  заменить  матрицей  ,  т.  к.  матрицы,  в  общем  случае,  не  коммутирующие. 

Использование  граничных  условий  для  многослойной  структуры  является  лишь  иной  формой  записи  уравнений  Максвелла  и  не  приводит  к  упрощению  решения  исходных  задач.  Вместе  с  тем,  решение  (1)  может  проводиться  стандартной  процедурой,  однотипной  для  различных  конфигураций  и  сред.  При  постоянных,  в  пределах  рассматриваемых  слоев,  элементах  матрицы    решение  ищется  в  виде  комбинации  функций:

,  ,

,.

Параметр    определяется  уравнением  ,  имеющим  в  общем  случае  четыре  комплексных  корня,  соответствующим  четырем  волнам  электромагнитного  поля  в  области  анизотропного  слоя  (две  распространяются  вдоль  оси  0z,  две  в  противоположном  направлении).  В  этом  случае  компоненты  поля  можно  представить  в  виде 

i=1,2,3,4,    –  постоянные,  определяемые  из  граничных  условий,  параметры    для  каждого  слоя  определяются  решением  систем  уравнений  следующего  типа: 

,

,

,

.

Условие  малой  толщины  слоя  позволяет  воспользоваться  разложением  матрицы  по  малому  параметру  и  получить  сравнительно  простые  расчетные  соотношения  для  большого  числа  структур. 

Для  многослойной  структуры  граничные  условия  примут  вид:

,  (2)

или  для  сокращения  записи  ,

где 

Условие  малой  толщины  слоя

  (3)

позволяет  воспользоваться  разложением  матрицы    по  малому  параметру  и  получить  сравнительно  простые  расчетные  соотношения.

Граничные  условия  (2)  могут  эффективно  использоваться  путем  деления  исследуемого  слоя  на  систему  тонких  пленок,  удовлетворяющих  соотношению  (3),  что  существенно  расширяет  возможности  двухсторонних  граничных  условий  для  аналитического  исследования  разнообразных  тонкопленочных  структур.  Элементы  матриц  рассеяния  для  каждого  слоя  структуры  в  этом  случае  имеют  вид:

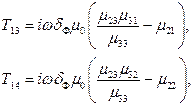
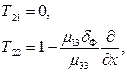
  (4)

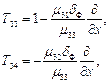
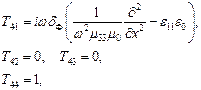
Воспользовавшись  методикой  можно  численно  рассчитать  частотные  зависимости  коэффициентов  прохождения  и  отражения  Е  и  Н-волн.  Данный  метод  расчета  дает  широкие  возможности  использования  его  для  предварительного  численного  моделирования  равномерной  амплитудно-  частотной  характеристики  фильтра,  на  основе  ферритовой  непериодической  структуры.

Список  литературы:

1. Глущенко  А.Г.,  Топоркова  Л.В.  Особенности  прохождения  электромагнитных  волн  через  ферритовые  пленки  с  произвольным  подмагничиванием  //  Физика  волновых  процессов  и  радиотехнические  системы.  –  2000.  –  том  3,  –  №  3–4.  –  С.  18–21.