ИССЛЕДОВАНИЕ  РЕЗОНАНСНЫХ  ЧАСТОТ  КОЛЕБАНИЙ  ПРИ  ПРИМЕНЕНИИ  РАЗЛИЧНЫХ  ГРАНИЧНЫХ  УСЛОВИЙ  В  ПАКЕТЕ  SOLIDWORKS.SIMULATION

Гришечкина  Мария  Григорьевна

студент 
Политехнического  института  Сибирского  Федерального  Университета, 
РФ,  г.  Красноярск

E-mail:  Mashka700@mail.ru

Колбасина  Наталья  Анатольевна

канд.  техн.  наук,  преподаватель 
Политехнического  института  Сибирского  Федерального  Университета, 
РФ,  г.  Красноярск

E-mail: 

RESONANCE  FREQUENCY  ANALYSIS  OF  THE  DIFFERENT  BOUNDARY  CONDITIONS  OF  THE  STAFT  WITH  SOLIDWORKS.SIMULATION

Maria  Grishechkina

student 
of  the  Polytechnic  Institute  of  the  Siberian  Federal  University, 
Russia,  Krasnoyarsk

Natalia  Kolbasina

candidate  of  Science,  teacher 
of  the  Polytechnic  Institute  of  the  Siberian  Federal  University, 
Russia,  Krasnoyarsk

АННОТАЦИЯ

В  данной  работе  рассматривается  влияние  различных  принципов  разработки  расчётной  конечно-элементной  модели  на  спектры  резонансных  частот  при  исследовании  динамических  характеристик  элементов  технических  систем.  Выявлены  различные  сочетания  граничных  условий  исключающих  разделение  форм  колебаний.  Кроме  того,  выявлена  возможность  выделения  участка  спектра,  состоящего  из  частот,  относящихся  только  к  одному  виду  колебаний. 

ABSTRACT

This  study  examines  the  effect  of  various  design  principles  for  calculated  finite-element  model  on  the  ranges  of  resonant  frequencies  in  the  study  of  the  dynamic  characteristics  for  the  elements  of  technical  systems.  There  were  revealed  various  combinations  of  boundary  conditions  excluding  the  sharing  of  waveforms.  Also  revealed  the  possibility  for  allocating  a  part  of  the  spectrum  consists  of  frequencies  belonging  only  to  one  kind  of  waves  was  hesitation.

Ключевые  слова:  резонансные  частоты;  формы  колебаний;  конечно-элементные  методы;  граничные  условия;  технические  системы.

Keywords:  resonant  frequencies;  waveform;  finite  element  methods;  boundary  conditions;  technical  systems.

При  разработке  различных  механизмов  на  этапе  проектирования  необходимо  оценивать  динамическое  качество  изделий.  При  разработке  автоматизированных  систем  проектирования  изделий  особую  важность  представляет  собой  управление  спектром  собственных  частот  будущей  механической  системы  с  помощью  изменения  параметров,  таких  как  геометрические  параметры  системы,  свойства  материала,  а  также,  конструктивные  особенности  исполнения,  выражающиеся  в  различных  способах  задания  граничных  условий  различных  элементов  системы.  При  этом  необходимо  иметь  в  виду,  что  возможность  провести  частотный  анализ  аналитически  осуществляется  не  всегда,  ввиду  сложности  конструкции.  Кроме  того,  не  всегда  представляется  возможным  разделить  задачу  на  определение  форм  колебаний  вдоль  той  или  иной  оси  или  координатной  плоскости.  В  частности,  при  исследовании  валов  часто  выделяют  только  поперечные  формы  колебаний,  только  осевые  или  только  крутильные,  что  невозможно  в  случае  одновременного  приложения  разнонаправленных  нагрузок.  В  сложной  форме  конструкции  предлагается  использовать  конечно-элементные  методы  для  определения  частотных  характеристик  системы,  что  позволяет  делать  анализ  намного  проще  и  быстрее.  В  таком  случае  особое  внимание  следует  уделить  корректности  моделирования  граничных  условий  и  нагрузок  при  решении  конечно-элементных  задач. 

В  данной  работе  определялись  резонансные  частоты  стержня.  При  этом  оценивался,  как  спектр  собственных  частот,  так  и  формы  колебаний  объектов  и  исследовались  влияния  различных  видов  моделируемых  закреплений  на  спектр  получаемых  резонансных  частот  и  распределение  в  этом  спектре  частот  различных  типов  колебаний

Расчёты  проводились  в  SolidWorks  программный  комплексе  САПР  для  автоматизации  работ  промышленного  предприятия  на  этапах  конструкторской  и  технологической  подготовки  производства.  Пакет  SolidWorks.  Simulation  позволяет  проводить  различные  типы  анализов,  таких  как  структурный,  частотный  и  другие.  Так  же  в  этом  пакете  можно  исследовать  не  только  отдельные  детали,  но  и  сборки,  например,  на  устойчивость.  При  нелинейном  анализе  могут  учитываться  различные  свойства  материала,  нелинейное  нагружение  и  т.  д.  [1].  Исследуемый  пакет  решает  задачи  с  помощью  метода  конечных  элементов  [2],  что  позволяет  производить  расчёты  достаточно  быстро. 

Метод  конечных  элементов  представляет  собой  наиболее  распространенный  приближенный  метод  в  механике  твердого  тела  и  может  быть  интерпретирован  с  физической  или  математической  точки  зрения.  Множество  элементов,  на  которые  разбита  конструкция,  называется  конечно-элементной  сеткой.  Механическое  поведение  каждого  элемента  выражается  с  помощью  конечного  числа  степеней  свободы  или  значений  искомых  функций  во  множестве  узловых  точек.  Поведение  математической  модели,  таким  образом,  аппроксимируется  поведением  дискретной  модели,  полученной  путем  сборки  всех  элементов  [2]. 

Для  верификации  разработки  расчетной  конечно-элементной  модели  была  решена  тестовая  задача  для  определения  собственных  частот  стержня  без  граничных  условий  и  нагрузок  [2].  Частоты  приведены  в  таблице  1.  Было  установлено  соответствие  с  результатами  аналитического  расчета  частот  при  поперечных  колебаниях  с  относительной  погрешностью  менее  5  %.

Таблица  1.

Собственные  частоты  стержня  без  граничных  условий

Однако,  необходимо  отметить,  что  в  данной  спектре  частот  были  определены  частоты,  не  только  соответствующие  поперечным  колебаниям,  а  также  осевые  и  крутильные.  Визуализация  форм  колебаний  соответствующим  разным  видам  представлены  на  рисунках  1,2  и  3.

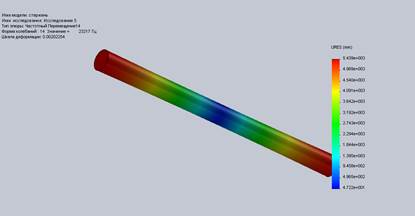
Рисунок  1.  Продольные  колебания  стержня  четырнадцатой  формы  безграничных  условий

Рисунок  2.  Крутильные  колебания  стержня  шестой  формы  без  граничных  условий

Рисунок  3.  Поперечные  колебания  стержня  десятой  формы  без  граничных  условий

На  рисунках  1,  2  и  3  видно,  что  колебания  действительно  разделяются,  при  отсутствии  граничных  условий  и  нагрузок. 

Сочетание  нескольких  видов  граничных  условий,  то  есть  сложные  граничные  условия,  что  в  технике  бывает  очень  часто,  приводит  к  тому,  что  формы  собственных  колебаний  перестают  разделяться  на  классические  поперечные,  продольные  и  крутильные,  формы  собственных  колебаний  становятся  сложными,  включающими  в  себя  некоторые  их  сочетания,  что  можно  видеть  на  рисунке  4,  5  и  в  таблице  2.

Рисунок  4.  Комбинированная  форма  колебаний  стержня  при  граничных  условиях:  с  одного  торца  –  зафиксированной  геометрией  и  по  всей  цилиндрической  поверхности  –  ролик/ползун

Рисунок  5.  Крутильные  и  поперечные  колебания  стержня  третьей  формы  при  граничных  условиях:  с  одного  торца  –  зафиксированной  геометрией  и  по  всей  цилиндрической  поверхности  –  ролик/ползун

Таблица  2.

Собственные  частоты  стержня  с  граничными  условиями:  с  одного  торца  зафиксированная  геометрия  и  по  всей  поверхности  –  ролик/ползун

На  рисунках  4,  5  и  в  таблице  2  наблюдаются  сочетания  продольных  и  крутильных  колебаний,  что  говорит  о  том,  что  при  правильном  применении  граничных  условий  можно  выделить  сочетания  тех  колебаний,  которые  нам  необходимы. 

В  общем  случае  при  сложных  граничных  условиях  частоты  различных  форм  колебаний  не  разделяются,  а  потому  говорить  отдельно  о  поперечных,  или  только  о  крутильных  не  правомочно.  И  в  каждом  отдельном  случае  для  конкретной  механической  системы  необходимо  индивидуально  подходить  к  вопросу  о  возможности  разделения  спектров  частот  различных  форм  колебаний.  Преимущества  конечно-элементных  методов  в  том,  что  такой  необходимости  не  возникает,  проведя  анализ  при  заданных  существующих  условиях,  мы  можем  проанализировать  получившийся  реальный  частотный  спектр  и  особенности  форм  колебаний,  соответствующих  каждой  интересной  для  исследования  частоте. 

Кроме  того,  меняя  и  комбинируя  различные  виды  граничных  условий  можно  смоделировать  ситуации,  когда  частотный  спектр,  в  заданном  диапазоне,  будет  содержать  частоты,  соответствующий  заданному  виду  колебаний.  Например,  исключить  поперечные  и  осевые  колебания,  для  получения  только  крутильных.  К  примеру,  подобную  методику  можно  применить  при  проектировании  выходного  звена  шпиндельного  станка  высокой  точности,  где  необходимо  исключить  поперечные  колебания  в  заданном  диапазоне  возмущающего  воздействия. 

  Ни  рисунках  6  и  7  применено  граничное  условие  зафиксированное  шарнирное  опирание,  при  таких  граничных  условиях  исключаются  продольные  колебания,  так  как  точкам  поверхности  при  нем  невозможно  перемещаться  в  радиальном  и  осевом  направлении  [1].  При  таких  граничных  условиях  выделяются  только  крутильные  колебания,  что  мы  и  наблюдаем  в  таблице  3,  единственное  что  меняется  –  число  полуволн. 

Рисунок  6.  Крутильные  колебания  стержня  третьей  формы  при  граничных  условиях:  по  всей  цилиндрической  поверхности  –  зафиксированный  шарнир

Рисунок  7.  Крутильные  и  поперечные  колебания  стержня  шестнадцатой  формы  при  граничных  условиях:  по  всей  цилиндрической  поверхности  –  зафиксированный  шарнир

Таблица  3.

Собственные  частоты  стержня  с  граничными  условиями:  по  всей  поверхности  –  зафиксированная  геометрия

Таким  образом,  мы  можем  сделать  вывод,  что  граничные  условия,  их  вид,  комбинации  существенным  образом  влияют  на  спектры  резонансных  частот.  При  проектировании  сложных  механических  систем  необходимо  учитывать,  что  не  всегда  возможно  разделение  частот  по  видам  колебаний,  что  усложняет  возможности  анализа  динамического  качества  проектируемых  изделий.  С  другой  стороны  комбинируя  различные  виды  граничных  условий  можно  добиться  необходимого  поведения  того  или  иного  элемента  конструкции,  то  есть  управлять  динамическими  свойствами  изделий  на  этапе  проектирования. 

Список  литературы:

1. Алямовский  А.А.  SolidWorks\CosmosWorks.  Инженерный  анализ  методом  конечных  элементов,  –  М.:  ДМК  Пресс,  2004.  –  432  с.:  ил.  (Серия  «проектирование»). 
2. Зенкевич  О.,  Морган  К.  Конечные  элементы  и  аппроксимация:  Пер.  с  англ.  –  М:  Мир,  1986.  –  318  с.
3. Тимошенко  С.П.,  Гудьер  Дж.  Теория  упругости:  Пер.  с  англ.  –  М.:  Наука,  1979.  –  560  стр.