ВЛИЯНИЕ  ЧАСТОТЫ  ЭЛЕКТРИЧЕСКОГО  ПОЛЯ  НА  ПОЛЯРИЗУЕМОСТЬ  НАНОЧАСТИЦ  АЛМАЗА  В  ВОДЕ

Войтылов  Алексей  Владиславович

канд.  физ.-мат.  наук,  старший  научный  сотрудник 
Санкт-Петербургского  Государственного  Университета, 
РФ,  г.  Санкт-Петербург

E-mail:  voivv@mail.ru

Петров  Михаил  Павлович

старший  преподаватель 
Санкт-Петербургского  Государственного  Университета, 
РФ,  г.  Санкт-Петербург

E-mail:  mihaeles@list.ru

Трусов  Анатолий  Анатольевич

д-р  физ.-мат.  наук,  профессор 
Санкт-Петербургского  Государственного  Университета, 
РФ,  г.  Санкт-Петербург

E-mail:  trusov@mail.ru

Войтылов  Владислав  Викторович

д-р  физ.-мат.  наук,  профессор 
Санкт-Петербургского  Государственного  Университета, 
РФ,  г.  Санкт-Петербург

E-mail:  vojtylov@gmail.com

Клемешев  Сергей  Алексеевич

старший  инженер 
Санкт-Петербургского  Государственного  Университета, 
РФ,  г.  Санкт-Петербург

E-mail: 

FREQUENCY  INFLUENCE  OF  ELECTRIC  FIELD  ON  POLARIZABILITY  OF  DIAMOND  NANOPARTICLES  IN  WATER

Alexey  Voitylov

candidate  of  science,  senior  researcher  at

Saint  Petersburg  State  University, 
Russia,  Saint-Petersburg

Mikhail  Petrov

candidate  of  science,  senior  teacher  at

Saint  Petersburg  State  University, 
Russia,  Saint-Petersburg

Anatoly  Trusov

doctor  of  science,  professor  at

Saint  Petersburg  State  University, 
Russia,  Saint-Petersburg

Vladislav  Vojtylov

doctor  of  science,  professor  at

Saint  Petersburg  State  University, 
Russia,  Saint-Petersburg

Sergey  Klemeshev

senior  engineer  at

Saint  Petersburg  State  University, 
Russia,  Saint-Petersburg

Работа  выполнена  при  финансовой  поддержке  гранта  СПбГУ  «Самоорганизующиеся  многокомпонентные  структуры  в  растворах  и  расплавах»,  11.38.267.2014  и  технической  поддержке  МРЦ  СПбГУ.

  Авторы  выражают  благодарность  Калганову  В.Д.  и  Волковой  А.В.  за  помощь  в  электронно-микроскопических  и  электрофоретических  измерениях.

АННОТАЦИЯ

В  настоящей  работе  были  исследована  поляризуемость  частиц  алмаза  (100—1000  нм)  в  водных  взвесях.  Экспериментально  исследовано  влияние  частоты  внешнего  электрического  поля  на  величину  электрооптического  эффекта  в  диапазоне  до  4  МГц.  Получены  дисперсионные  зависимости  анизотропии  поляризуемости  наночастиц  алмаза.  Аналогичные  зависимости  рассчитаны  теоретически  и  сопоставлены  с  результатами  эксперимента.  Расчитанные  и  измеренные  дисперсионные  кривые  анизотропии  поляризуемости  наночастиц  алмаза  согласуются  в  области  частот  выше  1  кГц.

ABSTRACT

Polarizability  of  diamond  nanoparticles  (100—1000  nm)  suspended  in  water  was  studied.  Frequency  dependence  of  electro-optical  effect  of  diamond  suspensions  was  measured  in  range  up  to  4  MHz.  It  was  used  to  plot  the  dispersion  curve  of  polarizability  anisotropy.  The  dispersion  curve  of  polarizability  anisotropy  was  also  calculated  theoretically.  The  comparison  of  experimental  and  theoretical  curves  was  made.  It  was  shown  that  these  curves  are  in  a  good  agreement  in  range  upper  1  kHz  .

Ключевые  слова:  частицы  алмаза;  водный  коллоид;  электрооптический  эффект;  поляризуемость  частиц;  дисперсия  поляризуемости.

Keywords:  Diamond  particles;  aqueous  colloid;  Electro-optical  effect;  particle  polarizability;  polarizability  dispersion.

Введение

Данная  работа  является  продолжением  ранее  начатых  электрооптических  исследований  нанодисперсных  систем  алмаза,  содержащих  частицы  неправильной  формы  в  области  размеров  от  нескольких  десятков  до  тысячи  и  более  нанометров  взвешенных  в  водной  среде  [1].  Интерес  к  таким  системам  продиктован  широким  их  использованием  в  ряде  технологий  и  их  необычными  свойствами,  которые  проявляются  в  образовании  структур  из  частиц  алмаза.  На  характер  взаимодействия  между  частицами  влияют  их  поверхностный  электрический  заряд,  а  также  постоянная  и  наведенная  поляризация.  Цель  данной  работы  проанализировать  в  какой  степени  существующая  теория  поляризуемости  коллоидных  частиц,  обладающих  двойным  электрическим  слоем  применима  к  определению  поляризуемости  коллоидной  частицы  алмаза  в  воде.  Частично  такая  проверка  проводилась  при  частотах  в  несколько  килогерц  [8],  когда  диффузная  часть  двойного  электрического  слоя  частиц  в  основном  и  определяет  их  поляризуемость.  В  данном  исследовании  рассмотрено  влияние  частоты  поля  приложенного  к  частице  на  её  поляризуемость  в  более  широкой  области  частот.

Исследованная  система  и  её  свойства

Выбранная  для  исследования  система  содержала  частицы,  взвешенные  в  водном  электролите,  форма  которых  напоминала  гранитный  щебень.  Электронно-микроскопические  снимки  показали,  что  в  процессе  подготовки  проб  частицы  при  высыхании  капель  системы  на  кварцевой  подложке  образуются  структуры  кластерного  типа.  Один  из  таких  снимков  представлен  на  рис.  1.

Рисунок  1.  Электронно-микроскопический  снимок  высохшей  капли  с  частицами  алмаза

Образование  таких  структур  в  коллоиде  мешало  бы  исследованию  поляризуемости  отдельных  частиц.  Для  исследования  приготавливались  сильно  разбавленные  системы,  агрегаты  из  частиц  в  которых  разбивались  периодическим  взбалтыванием  и  ультразвуковой  обработкой,  а  мелкие  частицы  из  дисперсной  фазы  убирались  центрифугированием.  Среднее  расстояние  между  частицами  более  чем  на  десятичный  порядок  превышало  их  размеры.  Счетная  концентрация  частиц  в  исследованных  системах  варьировалась  в  пределах  10⁹  –  10¹⁰  см^-3.  По  электронно-микроскопическим  снимкам  можно  определить  их  распределение  по  размерам,  понимая  под  размерами  частиц  их  радиусы  .  Полагаем,  что    —  это  радиус  круга,  имеющего  ту  же  площадь,  что  и  проекция  частицы  на  подложку.  Гистограмма  распределения  частиц  по  размерам    представлена  на  рис.  2.

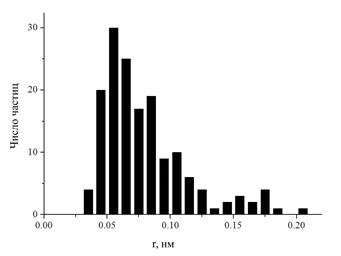
Рисунок  2.  Плотность  расспределения  частиц  по  их  радиусам

Частицы  алмаза  не  обладают  внутренней  анизотропией,  и  направлению  их  наибольшей  поляризуемости  будет  отвечать  направление  их  максимального  размера.  Обозначим  половину  этого  размера  ,  а  половину  среднего  размера  в  перпендикулярном  направлении  .  Будем  полагать,  что  поляризуемость  и  вязкое  трение  частицы  алмаза  в  воде  близка  к  поляризуемости  и  вязкому  трению  сфероида  с  полуосями    и  .  Отношение  полуосей  частиц    можно  оценить  из  их  снимков.  Как  для  более  крупных,  так  и  для  более  мелких  частиц,  исследованных  нами,  1.1<p<2,  а  среднее  значение  этого  отношения  <p>=1.5.  При  получении  коллоидов  использована  дистиллированная  вода,  но  для  получения  среды,  в  которой  основной  состав  ионов  известен  приготавливался  раствор  с  концентрацией  в  нем    310^-5  Моль/л.  Для  исследованных  взвесей  алмаза  электропроводность  и  кислотность  составляли  K=10  МОм^-1см^-1  и  pH=6.09.  Эти  характеристики  коллоидов  оставались  прежними  при  варьировании  концентрации  частиц.  Такие  системы  не  меняли  оптических  и  электрооптических  свойств  в  течение  недели  и  более.  Электрофоретическая  подвижность  частиц  в  системах  составляла  2.5810^-8  м²В/с,  а  рассчитанный  по  ней,  согласно  теории  Гельмгольца-Смолуховского,  электрокинетический  потенциал  =36,4  мВ.

Техника  и  методика  эксперимента

В  данных  исследованиях  мы  ограничились  измерениями  зависимостей  консервативного  дихроизма  от  величины  и  частоты  вызывающего  его  поля.  Так  как  для  экспериментов  такого  типа  серийной  аппаратуры  не  имеется,  была  создана  экспериментальная  установка,  в  которой  узкий  пучок  неполяризованного  света  проходил  между  плоскопараллельными  электродами  ячейки  Керра,  заполненной  исследуемым  коллоидом.  Прошедший  пучок  света  разбивался  на  два,  первый  из  них  линейно  поляризован  вдоль  напряженности  поля  между  электродами  ячейки,  а  второй  ортогонально  ей.  Интенсивности    и    первого  и  второго  пучков,  соответственно,  регистрировались  и  сравнивались.  При  отсутствии  поля  в  ячейке  они  равны,  однако  если  в  рассеивающей  свет  системе  полем  создать  упорядоченную  ориентацию  частиц,  то  прошедший  свет  становится  частично  поляризованным,  и  интенсивности    и    различаются,  если  размеры  частиц  соизмеримы  с  длинами  волн  падающего  света.  В  системе  с  частицами,  не  обладающими  анизотропией  поглощения,  наблюдается  консервативный  дихроизм  в  электрическом  поле  [4].  Величину    дихроизма  можно  определить  как  произведение  разности  констант  мутности  для  пучков  света,  выделенных  поляризаций,  на  длину  используемой  ячейки  Керра.  В  результате

.                                               (1)

Если  частицы  слабо  ориентированы  полем,  то  справедливо  соотношение  [8]

,                                 (2)

где:    —  значение    при  полной  ориентации  всех  частиц  вдоль  поля; 

  —  напряженность  поля  в  ячейке; 

  —  тепловая  энергия; 

  —  диэлектрическая  проницаемость  дисперсионной  среды.  При  определении  средней  анизотропии  поляризуемости  частиц  ,  входящей  в  (2),  необходимо  учитывать  функцию  распределения  частиц  с  дихроическим  весом  [7].  А  именно,

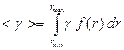.                                          (3)

Здесь:    —  анизотропия  поляризуемости  отдельной  частицы;  ;    —  дихроический  вес  частиц;    —  плотность  их  распределения  по  .  Функция    распределения  частиц  с  дихроическим  весом  может  быть  определена  при  изучении  зависимостей  эффекта    от  времени,  созданного  в  ячейке  слабыми  бисинусоидальными  полями  [9],  либо  сильными  полями  коротких  импульсов  [5].  Нормировка    определяется  соотношением

.

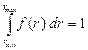Неизменность  функции    может  служить  критерием  того,  что  система  не  коагулирует  в  процессе  исследований.

Поляризуемость  частиц,  элементы  теории

Теория  поляризуемости  коллоидной  частицы  учитывает  образование  её  диполя  в  поле  как  за  счёт  поляризации  вещества  частицы,  так  и  прилегающего  к  ней  двойного  электрического  слоя  [6].  Здесь  представлены  основные  соотношения  для  сфероидальной  и  внутренне  изотропной  частицы.  Тензор  поляризуемости  такой  частицы  в  ее  собственной  системе  координат,  связанной  с  полуосями  сфероида,  имеет  две  компоненты    и  ,  отвечающие  поляризуемости  частиц  вдоль  полуосей    и  ,соответственно.  Компоненты    и    учитывают  фазовую  задержку  между  полем  и  поляризацией  частиц  в  рамках  теорий  Максвелл-Вагнера  и  α-дисперсии  и  могут  быть  представлены  в  комплексном  виде.  Входящая  в  (3)  анизотропия  поляризуемости    определяется  разностью

.

Обобщенные  формулы,  учитывающие  влияние  круговой  частоты  поля    на  поляризуемость,  имеют  вид  [6]

,                 (4)

где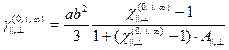 

и  при  ,

,  ,  .

Параметры    для  разных  составляющих  элементов  тензора  поляризуемости  определяется,  соответственно,  диэлектрическими  проницаемостями  частиц  и  дисперсионной  среды    и  ,  значениями  их  электропроводности  и    и  поверхностной  проводимости  .  Они  равны:    в  случае  ;    в  случае    ;    в  случае  .  Коэффициенты    и  зависят  только  от  размеров  частиц  и  равны

,    .

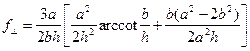Множители    во  втором  и  третьем  слагаемых  (4)  в  случае  синусоидального  поля  определяется  соотношением 

,                                                     (5)

в  котором  характерное  время  релаксации    в  разных  областях  дисперсии  различное.  В  области  Максвелл-Вагнеровской  дисперсии  оно  определяется  соотношением

.

В  области  α-дисперсии  для  оценки    достаточно    умножить  на  квадрат  отношения  размера  частицы  к  толщине  дебаевского  радиуса  экранирования  её  двойного  электрического  слоя  [2],  который  может  быть  рассчитан  для  заданного  электролита.  Формулы  для  строгого  определения  времени  релаксации    поляризуемости  в  области  α-дисперсии  приведены  в  работе  [6].  Если  к  коллоиду  приложено  поле,  не  имеющее  форму  синуса,  то  входящие  в  (4)  множители  не  определяются  соотношением  (5).  Однако,  используя  Фурье  преобразование  его  нетрудно  определить,  и  в  случае  использования  импульсов  прямоугольной  формы  можно  записать  в  виде

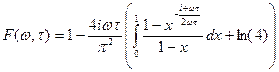.                              (6)

Данные  формулы  были  использованы  для  расчета  анизотропии  поляризуемости  частиц  алмаза  в  водном  растворе  KCl,  приготовленном  для  экспериментальных  исследований.  Рассмотрено  влияние  частоты  поля    на  анизотропию  поляризуемости  в  полях  синусоидальной  и  прямоугольной  формы.  Для  малых  средних  и  больших  частиц  алмаза,  вносящих  вклад  в  наблюдаемый  электрооптический  эффект,  дисперсионные  зависимости    в  случае  синусоидального  поля  представлены  на  рис.  3.

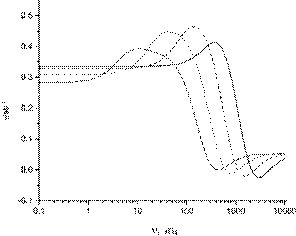
Рисунок  3.  Дисперсионные  зависимости  рассчитанные  при    =  50  (сплошная  линия)  ,  100  (пунктир),  200  (точки)  и  400  (штрих-пунктир)  нм 

Как  видно  из  рисунка  дисперсионные  зависимости  содержат  максимум  и  минимум.  Согласно  теории,  в  области  частот  нескольких  десятков  герц,  как  вещество,  так  и  двойной  электрический  слой  частиц  поляризованы,  а  действующее  на  частицу  поле  частично  экранировано  диффузионным  слоем  частиц.  Повышение  частоты  внешнего  поля  снижает  экранирование  и    достигает  максимального  значения.  При  дальнейшем  повышении  частоты  поляризация  двойного  слоя  уменьшается,  зависимость    спадает,  начиная  с  частот  ~  (0,1—1)  МГц  она  полностью  отсутствует.  В  этой  области  наблюдается  Максвелл-Вагнеровская  дисперсия  поляризуемости  и  зависимость    проходит  через  минимум.  Как  видно  из  рисунка,  линейная  зависимость  поляризуемости  частиц  от  их  объема  наблюдается  только  при  частотах  выше  нескольких  мегагерц,  а  при  более  низких  частотах  —  сублинейная  зависимость.  В  случае  полей  прямоугольной  формы,  максимум,  зависимости    менее  выражен  и  при  повышении  электропроводности  дисперсионной  среды  он  практически  исчезает.

Экспериментальные  результаты

Были  исследованы  зависимости    от  частоты  поля  .  Электрооптический  эффект  создавался  полями  прямоугольной  формы  (меандр)  в  области  частот  от  5  Гц  до  4  МГц  (при  использовании  синусоидальных  полей  в  области  частот  в  несколько  Гц  интерпретация  экспериментальных  данных  затруднительна).  Рассчитанная  и  экспериментально  определенная  зависимости    от    представлены  на  рис.  4.

Рисунок  4.  Дисперсионные  зависимости  ,  экспериментально  определенная  (точки)  и  теоретически  рассчитанная  (сплошная  линия)

Для  построения  экспериментальной  зависимости    от    измерялись  зависимости    в  области  полей  В/см,  для  которых    меняется  пропорционально  .  Необходимые  для  определения    значения  ,  входящие  в  соотношение  (2),  определялись  при  использовании  полей  В/с.  Они  определялись  в  области  частот  Гц  и  были  пропорциональны  концентрации  частиц.  Для  расчета  зависимости    от    использовались  соотношения  (3)  и  (6).  Они  позволяют  рассчитать  аналогичную  зависимость  при  использовании  выше  упомянутой  теории  поляризуемости  коллоидной  частицы.  Необходимая  для  расчетов  функция  распределения    определялась  как  методом  коротких  импульсов  [5],  так  и  бисинусоидального  поля  [9].  Результаты  её  определения  обоими  методами  совпадают.

Представленная  на  рис.  4  теоретическая  зависимость  рассчитана  при  поверхностной  проводимости  частиц    Ом^-1.  Как  видно  из  рисунка  теоретическая  и  экспериментальная  зависимости    от    совпадают  при  частотах  в  1  кГц  и  более.  При  понижении  частоты,  в  области    кГц,  экспериментально  определенные  значения    существенно  понижаются,  проходят  через  минимум  и  начинают  снова  возрастать  при    Гц.  Значения  ,  рассчитанные  согласно  теории,  остаются  практически  без  изменения  в  этой  области  частот.  Различие  зависимостей    от    в  области  низких  частот,  полученных  электрооптическими  методами  и  теоретически  рассчитанных,  может  быть  связано  с  несколькими  причинами.  К  ним  можно  отнести  частичную  поляризацию  электродов  и  снижение  величины  действующего  на  частицы  поля,  а  также  влиянием  постоянного  дипольного  момента  частиц  в  полярных  средах  на  их  ориентацию  [3].

Заключение

Проведенные  исследования  водного  коллоида  алмаза  позволяют  заключить,  что  поляризуемость  частиц  алмаза  хорошо  описывается  использованной  теорией  в  области  частот  более  1  кГц,  а  дисперсионные  зависимости  электрооптического  эффекта  вполне  пригодны  для  определения  поверхностной  проводимости  частиц  алмаза  в  водных  электролитах.

Список  литературы:

1. Войтылов  А.В.,  Петров  М.П.,  Трусов  А.А.,  Войтылов  В.В.,  Клемешев  С.А.  Оптические  и  электрооптические  свойства  взвесей  наночастиц  алмаза  /  Технические  науки  от  теории  к  практике  —  Сб.  ст.  по  материалам  XXXII  междунар.  науч.-практ.  конф..  Новосибирск:  Изд.  «СибАК»,  —  2014.  —  №  3(28)  —  С.  148—162.
2. Стоилов  С.П.,  Шилов  В.Н.,  Духин  С.С.,  Сокеров  С.,  Петканчин  В.  Электрооптика  коллоидов.  /  Киев.  «Наукова  Думка»  —  1977.  —  200  c.
3. Толстой  Н.А.,  Спартаков  А.А.  Электрооптика  и  магнитооптика  дисперсных  систем.  /  СПб:  Изд-во  СПбГУ.  —  1996.  —  244  с.
4. Heller  W.  Anisotropic  Light  Scattering  of  Streaming  Suspensions  and  Solutions  .//  Rev.  Mod.  Phys.  —  1959.  —  Vol.  31,  —  №  4.  —  P.  1072—1077.
5. Klemeshev  S.A.,  Petrov  M.P.,  Trusov  A.A.,  Voitylov  A.V.  //  Journal  of  Physics:  Condensed  Matter.  2010.  —  Vol.  22,  —  №  49.  —  P.  494106_1-10.
6. Shilov  V.N.,  Borkovskaia  Yu.B.,  Budankova  S.N.  Thin  Double  Layer  Theory  of  the  Wide-Frequency  Range  Dispersion  of  the  Polarizability  of  Nonconducting  Spheroidal  Particles  /  Chap.2  in  “Molecular  and  Colloidal  Electro-Optics”,  chap.2,  CRC  Taylor  &  Francis.  —  2007.  —  Vol.  134.  —  P.  39—57.
7. Spartakov  A.A.,  Trusov  A.V.,  Voitylov  A.V.,  Vojtylov  V.V.  Electro-optics  of  polydisperse  colloids.  //  Chap.7.  in  “Molecular  and  Colloidal  Electro-Optics”,  ed.  By  Stoylov  S.  and  Stoimenova  M.,  London,  N.Y.:  CRC  Press.  —  2006.  —  P.  193—227.
8. Trusov  A.A.,  Vojtylov  V.V.  Electrooptics  and  conductometry  of  polydisperse  systems.  /  CRC  Press,  Boca  Raton,  London,  Tokyo,  —  1993.  —  145  p.
9. Vojtylov  V.,  T.  Zernova,  A.  Spartakov,  A.  Trusov,  and  A.  Voitylov  Determination  of  distribution  of  colloidal  particles  on  their  parameters  in  electro-optical  investigation  //  Colloids  and  Surfaces  A:  Physicochemical  and  Engineering  Aspects.  —  2002.  —  Vol.  209,  —  №  2.  —  P.  123—129.