Статья опубликована в рамках: XXXV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 05 октября 2015 г.)
Наука: Физика
Секция: Оптика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
БИСТАБИЛЬНОСТЬ АВТОМОДУЛЯЦИОННЫХ КОЛЕБАНИЙ В АВТОНОМНОМ ТВЕРДОТЕЛЬНОМ КОЛЬЦЕВОМ ЛАЗЕРЕ
Дудецкий Вадим Юрьевич
аспирант
Московского государственного университета имени М.В. Ломоносова,
РФ, г. Москва
E-mail:
BISTABILITY OF AUTOMODULATION VIBRATIONS IN AUTONOMOUS SOLID-STATE RING LASER
Vadim Dudetskiy
post-graduate student
of Lomonosov Moscow State University,
Russia, Moscow
АННОТАЦИЯ
На основе численного моделирования исследованы бистабильные автомодуляционные режимы генерации кольцевого чип-лазера на YAG:Nd с несимметричной обратной связью встречных волн через обратное рассеяние. В области параметрического резонанса между автомодуляционными и релаксационными колебаниями найдены две ветви бистабильных автомодуляционных режимов генерации.
ABSTRACT
Bistable automodulation oscillation modes of ring chip laser on YAG:Nd with nonsymmetrical back-coupling of counterpropagating waves through the backward scattering are studied on the basis of numerical simulation. Two branches of bistable automodulation oscillation modes are found in the sphere of parametric resonance between automodulation and relaxation oscillations.
Ключевые слова: Твердотельный кольцевой лазер; автомодуляционный режим генерации; динамический хаос; амплитудная невзаимность; частотная невзаимность; стохастический резонанс; бистабильность.
Keywords: solid-state ring laser; automodulation oscillation mode; dynamic chaos; amplitude nonreciprocity; frequency nonreciprocity; stochastic resonance; bistability.
Введение
Для твердотельных кольцевых лазеров (ТКЛ) с однородно уширенной линией усиления характерна сложная динамика генерации. В автономном ТКЛ наблюдаются разнообразные режимы генерации, различающиеся по временным, спектральным и поляризационным характеристикам излучения. При исследовании нелинейной динамики автономных кольцевых чип-лазеров одной из важных задач является выявление условий, при которых возникает бистабильность генерации. Бистабильные состояния представляют интерес при изучении нелинейных стохастических процессов в ТКЛ [2] и, в частности, стохастического резонанса в кольцевых лазерах [10; 11; 3].
В работе [2] было обнаружено, что при параметрах кольцевого чип-лазера, соответствующих области параметрического резонанса между автомодуляционными и релаксационными колебаниями, может возникать бистабильность автомодуляционных колебаний. Бистабильными оказываются автомодуляционный режим первого рода и квазипериодический автомодуляционный режим. В исследовании, проведенном в работе [2], не было изучено влияние амплитудной невзаимности резонатора на бистабильность и, кроме того, анализ был проведен не во всей области параметрического резонанса, а лишь в некоторой части этой области.
В настоящей работе в рамках векторной модели ТКЛ с помощью численного моделирования проводится детальный анализ бистабильных автомодуляционных колебаний, возникающих при несимметричной связи встречных волн в области параметрического резонанса между автомодуляционными и релаксационными колебаниями.
Найдены две ветви бистабильных состояний, в которых имеет место периодическая и квазипериодическая автомодуляция интенсивностей встречных волн, а также может возникать и динамический хаос.
Результаты исследований
В исследованиях использовалась векторная модель ТКЛ. При вычислениях часть параметров полагалась равной экспериментально измеренным параметрам исследуемого лазера.
Время релаксации для чип-лазера Nd:YAG равно T1=240 мкс. Ширина полосы резонатора определялась по релаксационной частоте ![]() . При превышении накачки над порогом
. При превышении накачки над порогом ![]() =0.218 в исследуемом лазере основная релаксационная частота равнялась
=0.218 в исследуемом лазере основная релаксационная частота равнялась ![]() = 98.5 кГц, что дает величину
= 98.5 кГц, что дает величину ![]() =4.37*108с-1. Значение поляризационного параметра
=4.37*108с-1. Значение поляризационного параметра ![]() =0.75 было определено (так же, как и в [6]) по экспериментально измеренной зависимости дополнительной релаксационной частоты
=0.75 было определено (так же, как и в [6]) по экспериментально измеренной зависимости дополнительной релаксационной частоты ![]() от частотной невзаимности резонатора
от частотной невзаимности резонатора ![]() .
.
Как было показано в работе в [1], в кольцевом чип-лазере можно изменять отношение модулей коэффициентов связи ![]() при регулировке температуры моноблока. В настоящей работе модуль одного из коэффициентов связи полагался равным
при регулировке температуры моноблока. В настоящей работе модуль одного из коэффициентов связи полагался равным ![]() кГц, а отношение
кГц, а отношение ![]() = 0.41. Разность фаз комплексных коэффициентов связи
= 0.41. Разность фаз комплексных коэффициентов связи ![]() трудно оценить по характеристикам автомодуляционных колебаний. Для простоты, разность фаз коэффициентов связи
трудно оценить по характеристикам автомодуляционных колебаний. Для простоты, разность фаз коэффициентов связи ![]() полагалась равной нулю. Величина амплитудной невзаимности кольцевого резонатора
полагалась равной нулю. Величина амплитудной невзаимности кольцевого резонатора ![]() варьировалась при численном моделировании, частотная невзаимность резонатора полагалась равной нулю.
варьировалась при численном моделировании, частотная невзаимность резонатора полагалась равной нулю.
В автономном кольцевом чип-лазере в широкой области лазерных параметров возникает автомодуляционный режим первого рода, для которого характерна противофазная синусоидальная модуляция интенсивностей встречных волн. Если частота автомодуляции ![]() близка к удвоенному значению основной релаксационной частоты, возникает ряд нелинейных эффектов, связанных с параметрическим взаимодействием автомодуляционных и релаксационных колебаний (параметрический резонанс). В этой области возникает неустойчивость автомодуляционного режима генерации первого рода, и возбуждаются более сложные автомодуляционные режимы генерации (в том числе, и режим динамического хаоса) [2; 4; 5; 7—9].
близка к удвоенному значению основной релаксационной частоты, возникает ряд нелинейных эффектов, связанных с параметрическим взаимодействием автомодуляционных и релаксационных колебаний (параметрический резонанс). В этой области возникает неустойчивость автомодуляционного режима генерации первого рода, и возбуждаются более сложные автомодуляционные режимы генерации (в том числе, и режим динамического хаоса) [2; 4; 5; 7—9].
При наличии амплитудной невзаимности кольцевого резонатора, связанной с неравенством модулей коэффициентов связи ![]() и неравенством добротностей резонатора для встречных волн
и неравенством добротностей резонатора для встречных волн ![]() , как было впервые показано в работе [2], в этой области может возникать бистабильность автомодуляционных режимов.
, как было впервые показано в работе [2], в этой области может возникать бистабильность автомодуляционных режимов.
Первая ветвь бистабильных автомодуляционных режимов
При изменении превышения накачки над порогом с h = 0.17 до h = 0.44 в зависимости от начальных условий наблюдаются две ветви автомодуляционных режимов генерации.
Обозначим их как Ветвь 1 и Ветвь 2, соответственно. Рассмотрим вначале Ветвь 1. В этом случае при h = 0.17 и ![]() кольцевой чип-лазер работал в автомодуляционном режиме первого рода. Значения превышения накачки над порогом далее последовательно увеличивались с шагом
кольцевой чип-лазер работал в автомодуляционном режиме первого рода. Значения превышения накачки над порогом далее последовательно увеличивались с шагом ![]() . При прохождении всего интервала по шкале
. При прохождении всего интервала по шкале ![]() изменялось значение амплитудной невзаимности, и расчет повторялся снова c превышения накачки над порогом h = 0.17 в указанных пределах (от h = 0.17 до h = 0.44). Значение амплитудной невзаимности варьировалось от 500 с-1 до 3000 с-1с шагом 250 с-1.
изменялось значение амплитудной невзаимности, и расчет повторялся снова c превышения накачки над порогом h = 0.17 в указанных пределах (от h = 0.17 до h = 0.44). Значение амплитудной невзаимности варьировалось от 500 с-1 до 3000 с-1с шагом 250 с-1.
На Ветви 1 при 0.17 <h< 0.22 наблюдается автомодуляционный режим первого рода. На рис. 1 показаны временная зависимость интенсивности излучения волны ![]() (а), а также спектр автомодуляционных колебаний (б).
(а), а также спектр автомодуляционных колебаний (б).
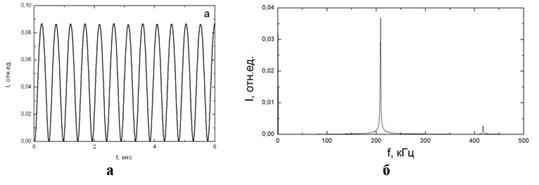
Рисунок 1. Временная зависимость интенсивности волны в автомодуляционном режиме первого рода (а) и спектр интенсивности (б) при и 500 с-1
В области 0.22 <h< 0.33 возникает периодический режим с удвоенным периодом автомодуляционных колебаний (см. рис. 2, а).
Для этого режима характерно появление в спектре выходного излучения дополнительной спектральной компоненты на частоте, равной половине автомодуляционной частоты (см. рис. 2, б).

Рисунок 2. Временная зависимость интенсивности волны в периодическом режиме с удвоенным периодом автомодуляционных колебаний (а) и спектр интенсивности (б) при и 500 с-1
В области 0.33 <h< 0.39 периодический автомодуляционный режим с удвоенным периодом автомодуляционных колебаний сменяется квазипериодическим режимом с удвоенным периодом автомодуляции (рис. 3).
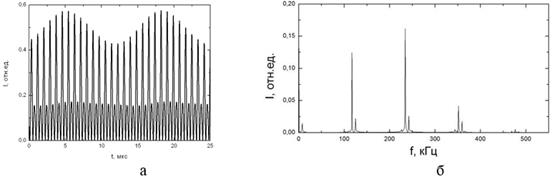
Рисунок 3. Временная зависимость интенсивности волны в квазипериодическим режимом с удвоенным периодом автомодуляции (а) и спектр интенсивности (б) при и 500 с-1
В этом режиме появляется огибающая амплитуды автомодуляционных колебаний (см. рис. 3, а), а в спектре выходного излучения, помимо спектральных компонент на автомодуляционной и релаксационной частотах, возникают также компоненты на частоте, равной половине автомодуляционной частоты.
Характерная зависимость интенсивности выходного излучения от времени и спектр автомодуляционных колебаний для этого режима показаны на рис. 3,а и 3,б.
При превышении накачки над порогом h>0.39 данный режим сменяется вновь автомодуляционным режимом первого рода.
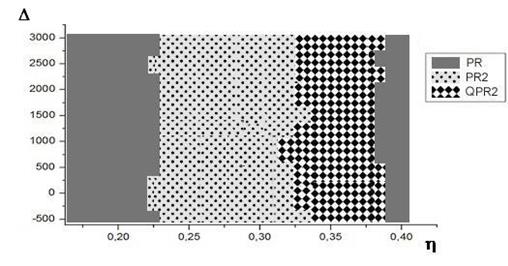
На рис. 4, в плоскости лазерных параметров (h,![]() ) показаны области существования автомодуляционных режимов генерации на Ветви 1.
) показаны области существования автомодуляционных режимов генерации на Ветви 1.
 а
а
Рисунок 4 а. Области существования автомодуляционных режимов генерации на Ветви 1 (а) в плоскости лазерных параметров (h,)
Вторая ветвь бистабильных автомодуляционных режимов
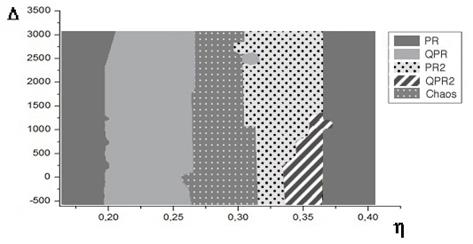
Для Ветви 2 эволюция автомодуляционных режимов генерации при изменении параметров h и![]() представлена на рис. 4, б.
представлена на рис. 4, б.
 б
б
Рисунок 4, б. Области существования автомодуляционных режимов генерации на Ветви 2 (б) в плоскости лазерных параметров (h,)
Как было ранее установлено в [2], в исследуемом кольцевом чип-лазере с несимметричной связью (![]() =0.4) при h> 0.19 помимо периодического автомодуляционного режима первого рода (PR) возникает квазипериодический автомодуляционный режим (QPR) Учитывая это, на Ветви 2 при h = 0.19 и
=0.4) при h> 0.19 помимо периодического автомодуляционного режима первого рода (PR) возникает квазипериодический автомодуляционный режим (QPR) Учитывая это, на Ветви 2 при h = 0.19 и ![]() задавались начальные условия, при которых возникает режим QPR. Значения превышения накачки над порогом далее последовательно увеличивались с шагом
задавались начальные условия, при которых возникает режим QPR. Значения превышения накачки над порогом далее последовательно увеличивались с шагом ![]() После прохождения всего интервала по параметру
После прохождения всего интервала по параметру ![]() , как и для Ветви 1, изменялось значение амплитудной невзаимности, и расчет повторялся при новом значении
, как и для Ветви 1, изменялось значение амплитудной невзаимности, и расчет повторялся при новом значении ![]() .
.
Как видно из рис. 4, б, квазипериодический режим QPR при ![]() существует в области превышений накачки над порогом 0.19 <h< 0.26. При увеличении амплитудной невзаимности
существует в области превышений накачки над порогом 0.19 <h< 0.26. При увеличении амплитудной невзаимности ![]() происходит сужение области существования режима QPR.
происходит сужение области существования режима QPR.
На рис. 5 показана характерная форма автомодуляционных колебаний интенсивности излучения одной из волн (а) и спектр интенсивности. В этом режиме помимо частоты автомодуляционных колебаний ![]() возбуждается основная релаксационная частота
возбуждается основная релаксационная частота ![]() , остальные компоненты спектра являются комбинационными частотами от двух этих основных частот.
, остальные компоненты спектра являются комбинационными частотами от двух этих основных частот.
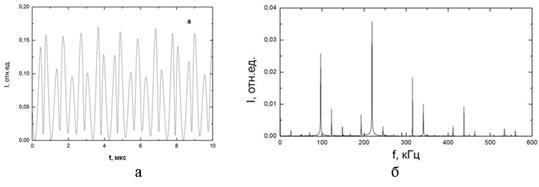
Рисунок 5. Временная зависимость интенсивности волны в квазипериодическом автомодуляционном режиме QPR (а) и спектр интенсивности (б) при и 250 с-1
С увеличением параметра h на Ветви 2, режим QPR переходит в режим динамического хаоса (Chaos), который при ![]() существует в области накачек 0.26 <h< 0.32.
существует в области накачек 0.26 <h< 0.32.
Как видно из представленных рисунков, амплитудная невзаимность слабо влияет на ширину области существования режима хаоса.
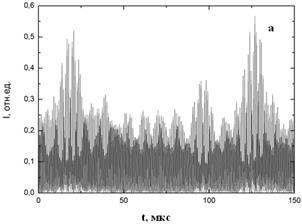
На рис. 6,а,б показаны временные зависимости интенсивностей встречных волн в режиме хаоса на двух интервалах времени (коротком и длинном).
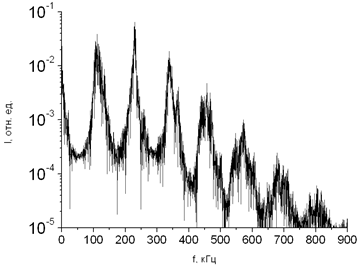
На рис..6, в показан спектр интенсивности одной из волн. Видно, что в этом режиме имеется характерная для режимов динамического хаоса область непрерывного спектра, на которой выделяется ряд дискретных частот, соответствующих автомодуляционным и релаксационным колебаниям.
На Ветви 2 в диапазоне превышений 0.32<h<0.37 возникают периодический автомодуляционный режим с удвоенным периодом PR2 и квазипериодический автомодуляционный режим QPR2.
Эти режимы аналогичны одноименным режимам, возникающим на Ветви 1. В области превышений накачки над порогом h > 0.37 бистабильность исчезает и наблюдается автомодуляционный режим первого рода (PR).
 а
а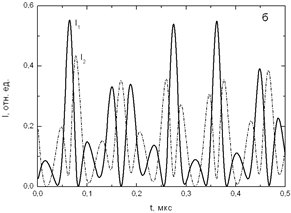 б
б
 в
в
Рисунок 6. Временные зависимости интенсивностей встречных волн в режиме динамического хаоса на коротком (а) и длинном (б) интервалах времени, а также спектр интенсивности волны в этом режиме (в) при и 250 с-1
Сравнение с экспериментом
Автомодуляционные режимы, возникающие в области параметрического резонанса, были исследованы ранее экспериментально. В этих работах были обнаружены лишь автомодуляционные колебания, возникающие на Ветви 1: периодический режим с удвоенным периодом автомодуляционных колебаний (PR2) и квазипериодический режим с удвоенным периодом автомодуляции (QPR2). Экспериментальные результаты хорошо согласуются с результатами численного моделирования для Ветви 1.
Ветвь 2, исследованная в настоящей работе, не наблюдалась ранее экспериментально. Исключение представляет лишь квазипериодический автомодуляционный режим, который удалось наблюдать косвенно при наличии шумовой модуляции накачки [2].
Исследования, проведенные в работе [2], показали, что на бистабильность автомодуляционных колебаний, возникающую при несимметричной связи встречных волн, оказывают сильное влияние флуктуации мощности накачки. При наличии даже слабого шума накачки квазипериодический автомодуляционный режим, как показано в [2], перестает наблюдаться.
Учитывая результаты этих исследований, можно предположить, что автомодуляционные режимы, относящиеся к Ветви 2, не удается наблюдать из-за технических флуктуаций мощности накачки.
Для наблюдения бистабильности в этом случае необходимо провести экспериментальные исследования при тщательной стабилизации излучения накачки и контроле уровня шумов (технических и естественных).
Кроме того, причина, почему в эксперименте не удалось наблюдать вторую ветвь, может быть связана те только с влиянием технических флуктуаций мощности накачки, но и с ограничениями на скорость изменения мощности накачки в использованном чип-лазере.
При проведении эксперимента в начале осуществляется генерация при накачке, близкой к пороговой, и в этом начальном состоянии в чип-лазере бистабиольтность отсутствует, так как возникающий автомодуляционный режим генерации находится далеко от области параметрического резонанса.
При увеличении накачки лазер переходит в область параметрического резонанса. Численное моделирование показывает, что медленный переход в область параметрического резонанса не позволяет реализовать экспериментальное наблюдение второй ветви. При медленном включении кольцевой чип-лазер будет всегда находиться на первой ветви генерации, то есть, медленное включение всегда будет приводить к тому, что реализуется лишь первая ветвь.
Выводы
В настоящей работе в рамках векторной модели ТКЛ с помощью численного моделирования проведен детальный анализ бистабильности автомодуляционных режимов генерации, возникающих в области параметрического резонанса между автомодуляционными и релаксационными колебаниями.
На основе проведенных исследований найдены области значений превышения накачки над порогом и величины амплитудной невзаимности, в которых возникает бистабильность автомодуляционных колебаний.
Найдены две ветви бистабильных состояний. На первой ветви наблюдаются периодические автомодуляционные режимы: автомодуляционный режим первого рода и режим с удвоенным периодом. Для второй ветви характерна более сложная динамика излучения
в зависимости от уровня накачки: с ростом превышения накачки над порогом генерации квазипериодический автомодуляционный режим переходит в режим динамического хаоса, затем в периодический автомодуляционный режим с удвоенным периодом, и, наконец, в автомодуляционный режим первого рода.
Список литературы:
- Аулова Т.В., Кравцов Н.В., Ларионцев Е.Г., Чекина С.Н. Квазипериодический режим автомодуляционных колебаний с низкочастотной импульсной огибающей. — Квантовая электроника, 41, 13 (2011).
- Золотоверх И.И., Кравцов Н.В., Ларионцев Е.Г., Чекина С.Н. Cтохастические эффекты при воздействии шума накачки на бистабильные автомодуляционные колебания в твердотельном кольцевом лазере. — Квантовая электроника, 39, 515 (2009).
- Золотоверх И.И., Кравцов Н.В., Ларионцев Е.Г., Фирсов В.В., Чекина С.Н. Экспериментальное наблюдение стохастического резонанса в твердотельном кольцевом лазере в отсутствие бистабильности. — Квантовая электроника, 39, 853 (2009).
- Золотоверх И.И., Кравцов Н.В., Кравцов Н.Н., Ларионцев Е.Г., Макаров А.А. Взаимодействие автомодуляционных и релаксационных колебаний и его роль в нелинейной динамике твердотельного кольцевого лазера. — Квантовая электроника, 24, 638 (1997).
- Золотоверх И.И., Ларионцев Е.Г. Параметрический резонанс в автономном твердотельном кольцевом лазере. — Квантовая Электроника, 22, 1171 (1995).
- Золотоверх И.И., Кравцов Н.В., Ларионцев Е.Г., Фирсов В.В., Чекина С.Н. Влияние различия поляризаций встречных волн на динамику твердотельных кольцевых лазеров. – Квантовая электроника, 37, 1011 (2007).
- Золотоверх И.И., Кравцов Н.В., Ларионцев Е.Г., Макаров А.А., Фирсов В.В. Новые механизмы возникновения динамического хаоса в твердотельном кольцевом лазере. — Квантовая электроника, 22, 213, (1995).
- Золотоверх И.И., Камышева А.А., Кравцов Н.В., Ларионцев Е.Г., Фирсов В.В., Чекина С.Н. Нелинейные процессы при удвоении периода автомодуляционных колебаний в кольцевом твердотельном лазере. — Квантовая Электроника, 38, 956 (2008).
- Kravtsov N.N., Lariontsev E.G. Nonlinear dynamics of solid-state ring laser. Laser Physics, 7, 196 (1997).
- Mс Namara B., Wiesenfeld K., Roy R. Observation of Stochаstic Resonance in a ring laser, Phys. Rev. Lett., 60, 2626 (1988).
- Vemuri G., Roy R. Stochastic resonance in a bistable ring laser. Phys. Rev. A, 39, 4668 (1989).
дипломов


Оставить комментарий