ГРУППОВАЯ  СКОРОСТЬ  ГИДРОАКУСТИЧЕСКОГО  ВОЛНОВОДА

Папкова  Юлия  Игоревна

канд.  физ.-мат.  наук,  доцент

ФГАОУ  ВО  Севастопольский  государственный  университет,

РФ,  г.  Севастополь

E-mail:  yulia.papkova@gmail.com

Папкова  Анна  Станиславовна

магистрант

ФГАОУ  ВО  Севастопольский  государственный  университет,

РФ,  г.  Севастополь

E-mail:  hanna.papkova@gmail.com

GROUP  VELOCITY  OF  HYDROACOUSTIC  WAVEGUIDE

Yulia  Papkova

PhD,  assistant  professor 
of  Sevastopol  State  University, 
Russia,  Sevastopol

Anna  Papkova

master 
of  Sevastopol  State  University, 
Russia,  Sevastopol

АННОТАЦИЯ

Рассматривается  влияние  донного  затухания  и  рефракционного  члена  профиля  скорости  звука  на  групповую  скорость  в  гидроакустическом  волноводе.  Поучено  аналитическое  представление  групповой  скорости  в  двухслойной  модели  гидроакустического  волновода.

ABSTRACT

Influence  of  bottom  attenuation  and  refraction  member  of  sounds  speed  on  group  velocity  in  the  hydroacoustic  waveguide  is  considered.  The  analytical  representation  of  group  velocity  is  presented  for  two-layer  model  of  hydroacoustic  waveguide.

Ключевые  слова:  групповая  скорость;  гидроакустический  волновод;  моды;  скорость  звука;  донное  затухание. 

Keywords:  group  velocity;  hydroacoustic  waveguide;  normal  modes;  sounds  speed;  bottom  attenuation. 

Введение

Для  моделирования  свойств  дна  волновода  используют  два  основных  подхода:  плоскослоистая  модель  на  абсолютно  жестком  основании  и  плоскослоистая  модель  на  жидком  полупространстве.  Данные  модели  приводят  к  разным  краевым  задачам  для  вертикального  волнового  уравнения.  В  случае  жесткого  дна  оператор  задачи  имеет  только  дискретную  часть  спектра,  для  жидкого  полупространства  оператор  имеет  также  и  непрерывную  составляющую  спектра  в  силу  того,  что  краевая  задача  формулируется  на  полуоси  .  Рассмотрим,  как  модель  дна,  донное  затухание  и  профиль  скорости  звука  влияют  на  групповую  скорость  в  волноводе.

Постановка  задачи

Для  исследования  основных  волноводных  эффектов  в  гидроакустическом  волноводе,  рассмотрим  двухслойную  модель  гидроакустического  волновода.  Расположим  начало  цилиндрической  системы  координат  на  поверхности  волновода  над  источником  звука  с  координатами  (0,  z₀),  ось  Oz  направлена  к  дну.  В  случае  цилиндрической  симметрии  звуковое  поле  точечного  гармонического  источника  излучающего  волну  круговой  частоты  ω,  описывается  скалярной  функцией  ,  удовлетворяющей  уравнению  Гельмгольца

где:  Δ  —  оператор  Лапласа; 

Ф  (r,  z)  —  амплитуда  потенциала  скорости; 

  —  дельта  функция  Дирака; 

c(z)  —  вертикальное  распределение  скорости  звука  в  волноводе.

Поверхность  волновода  моделируется  как  акустически  свободная,  что  соответствует  краевому  условию

На  границе  раздела  слоев  z  =  h  выполняются  условия  непрерывности  звукового  поля:

,

где:  r₁  —  плотность  слоя  воды; 

ρ₂  —  плотность  донных  осадков.

В  случае  наличия  затухания  γ  в  донном  слое  групповая  скорость  вычисляется  аналитически  как  отношение  среднего  потока  энергии  через  вертикальную  плоскость  r  =  const  к  средней  плотности  энергии,  находящейся  между  двумя  вертикальными  плоскостями,  отстоящими  друг  от  друга  на  расстоянии  2π/│Reξ│,  где  горизонтально‑волновые  числа  ξ  определяются  из  соответствующего  дисперсионного  уравнения  [2].  В  случае  наличия  постоянного  профиля  скорости  звука  как  в  водном  слое  с₁,  так  и  в  донном  слое  с₂  и  модели  дна  в  виде  жидкого  полупространства  групповую  скорость  можно  определить  как  [1;  2]

где  с_ф  —  фазовая  скорость  ;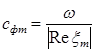

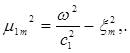
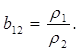
В  некоторых  случаях  удобней  аппроксимировать  жидкое  полупространство  слоем  конечной  толщины  (h₁‑h),  в  результате  получим  модель  гидроакустического  волновода,  дно  которого  расположено  на  абсолютно  –  жестком  основании.  При  достаточно  большой  глубине  жесткого  дна  h₁  выражения  для  групповой  скорости  совпадают  как  для  модели  волновода,  в  котором  дно  расположено  на  абсолютно  жестком  основании,  так  и  для  волновода,  у  которого  дно  представляет  собой  жидкое  полупространство.

Если    (),  тогда  ,  и  как  следствие  получаем

Аналогично  можно  показать,  что    и  .

Таким  образом,  непрерывная  составляющая  спектра  для  модели  жидкого  дна  не  влияет  на  групповую  скорость,  так  как  она  определяется  лишь  дискретным  спектром  волновода.

Численные  результаты.

В  табл.  1  приводятся  результаты  численных  расчетов  групповой  скорости  для  гидроакустического  волновода,  представляющего  собой  однородный  слой  воды  глубины  h=  150  м  с  профилем  скорости  звука  ,  второй  слой  —  грунт,  состоящий  из  ила  с  постоянным  профилем  скорости  звука  с₂  =  1474  м/с  и  c  затуханием  γ  =  0,009.  Отношение  плотностей  водного  слоя  и  слоя  осадков  полагаем  b₁₂  =  0,806,  частота  звука  f  =  50  Гц. 

Таблица  1.

Результаты  численных  расчетов  групповой  скорости

В  табл.  2  показано  влияние  частоты  на  групповую  скорость  гидроакустического  волновода.

Таблица  2. 

Влияние  частоты  на  групповую  скорость

Список  литературы:

1. Бреховских  Л.М.  Волны  в  слоистых  средах/Л.М.  Бреховских.  —  М.:  Наука,  1973.  —  343  с.
2. Buckingham  M.J.  On  the  acoustic  field  in  a  Pekeris  waveguide  with  attenuation  in  the  bottom  half‑space/  M.J.  Buckingham,  E.M.  Giddens  //  J.Acoust.Soc.Am.  —  2006.  —  №  1.  —  P.  123—142.