К ДИНАМИЧЕСКОЙ ТЕОРИИ БРЭГГОВСКОЙ ДИФРАКЦИИ ФЕМТОСЕКУНДНЫХ РЕНТГЕНОВСКИХ ИМПУЛЬСОВ ИЗОГНУТЫМИ КРИСТАЛЛАМИ

Чен Тэсик

доц., канд. физ.-мат. наук, Московский технологический университет,,

доц. кафедры физики отделения фундаментальной и инженерной химии,

РФ, г. Москва

E-mail: chen.tt@mail.ru

ON THE DYNAMICAL THEORY OF BRAGG-DIFFRACTION

OF X-RAY FEMTOSECOND PULSES BY BENT CRYSTALS

Chen Tasik

аssociated Professor, PhD, Moscow University of Technology,

Department of Fundamental and Engineering Chemistry, Chair of Physics,

Russia, Moscow

Аннотация

Представлена динамическая теория брэгговской пространственно-временной дифракции фемтосекундных рентгеновских импульсов совершенными изогнутыми кристаллами. Рассмотрен случай упругого изгиба кристалла по параболическому цилиндру. На основе рентгено-оптического принципа Гюйгенса-Гюйгенса-Френеля получено выражение для амплитуды дифрагированного импульса в вакууме.

ABSTRACT

Dynamical theory of Bragg spatial-temporal diffraction of femtosecond x-ray pulses by ideal bent crystals is presented. Homogeneous bending of a crystal on a parabolic cylinder is considered. Using an x-ray-optical Hyugens-Fresnel principle a formula for an amplitude of a diffracted pulse in vacuum is derived.

Ключевые слова: динамическая теория дифракции; упруго изогнутый кристалл; фемтосекундный импульс; рентгено-оптический принцип Гюйгенса-Френеля; пространственно-временная дифракция.

Keywords: dynamical theory of diffraction; an elastically bent crystal; femtosecond pulse; X-ray optical Hyugens-Fresnel principle; spatial-temporal diffraction.

В настоящее время интенсивно идут работы по созданию рентгеновского лазера на свободных электронах, излучающего в жестком рентгеновском диапазоне (l ~ 1Å). В связи с этим актуальность приобретает разработка способов управления характеристиками излучения лазера, основанных на динамической дифракции рентгеновского излучения в совершенных кристаллах. Динамическая теория зависящей от времени дифракции по Брэггу в совершенных плоских кристаллах была развита на основе формализма функций Грина в статье [4].

Динамическая теория дифракции излучения рентгеновского лазера совершенными кристаллами рассматривалась также в [5; 6]. В работах [1; 2] получила развитие общая теория динамической дифракции рентгеновского импульса с произвольной пространственно-временной структурой поля падающего импульса в кристаллах с произвольной толщиной в геометриях Брэгга и Лауэ. Одним из важных результатов этой теории явилась возможность временной компрессии фемтосекундных импульсов [3].

В данной работе развита динамическая теория пространственно-временной брэгговской дифракции рентгеновского импульса в толстом изогнутом кристалле. Амплитуду поля падающего импульса на входной поверхности кристалла представим в виде

E_inc (x, z = 0, t ) = E (x ) ,

где: c – скорость света, a = tg j ₀ – tg j _h ,

g₀ = cos j ₀ , j _{0, h} – направляющие косинусы для падающей и отраженной волн соответственно.

Ниже для определенности рассмотрим совершенный кристалл, подвергнутый механическому изгибу по параболическому цилиндру. Изгиб будем считать «слабым», что позволяет нам аппроксимировать функцию Грина изогнутого кристалла выражением для неизогнутого идеального кристалла.

Декартовы и косоугольные координаты связаны следующим образом:

Граничные условия для случая Брэгг-геометрии имеют вид

 Разлагая функцию F (t) в фурье-интеграл

F (t) = (2p)^-1 dw F (w ) exp(-i w t),

где фурье-трансформанта F (w ) равна

,

получим амплитуду дифрагированной волны на поверхности слабоизогнутого кристалла

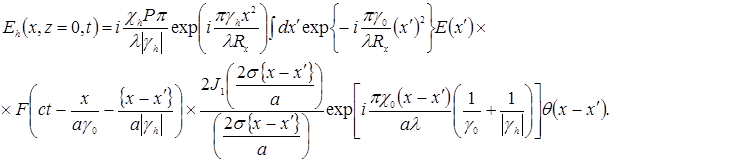(1)

Здесь P – поляризационный фактор, c_h,o – фурье-компоненты рентгеновской поляризуемости кристалла, R _x – радиус изгиба кристалла, s = p/L, L – экстинкционная длина, J₁ (x) – функция Бесселя первого порядка, q( x) – ступенчатая функция Хевисайда.

Рассмотрим импульс, квадратично промодулированный по фазе F (t) = exp (ibt² ) и с квадратичной фазой по координате x для функции E (x ).

 Дифрагированное поле на поверхности кристалла

(2)

где: A₁ =  ,

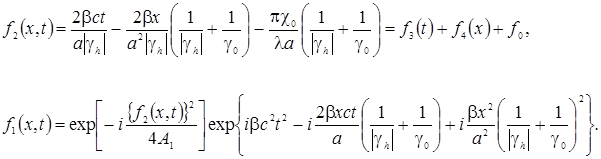
Интеграл в (2) вычисляется с помощью метода стационарной фазы. Интенсивность отраженного импульса I_h = | E_h |² определяется квадратом модуля функции G_h (k) в стационарной точке k_stat = – ¦₂ (x, t) – 2 A₁ x, зависящей от координаты и времени.

Поле отраженного импульса на расстоянии L_h от кристалла в точке с поперечной координатой x _p имеет следующий вид

E_h (r_p, t )exp(ik_h r_p) = 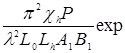{iæ(L₀+ L_h}exp exp(ibc²t²)´

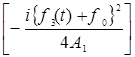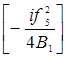
´expexpexp ´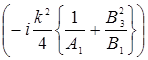

´exp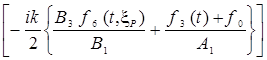, (3)

,

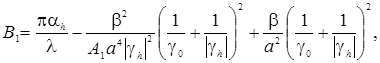
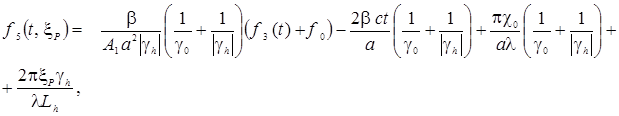
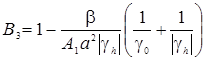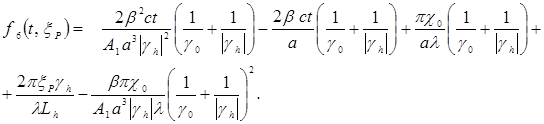
В случае, если в (3) исчезают квадратичные по k члены эйкональной функции, происходит фокусировка дифрагированного импульса в вакууме.

Условие фокусировки импульса имеет следующий вид

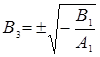.                                                          (4)

Из (4) видно, что для пучка, промодулированного по фазе, в принципе возможно образование двух фокусов.

Распределение интенсивности вблизи изображения источника определяется функцией Бесселя первого порядка.

При b = 0 условие пространственной фокусировки принимает вид: , откуда следует, что a₀ = - a_h .

Таким образом, можно сделать вывод о том, что использование принципов динамической дифракции рентгеновского излучения на изогнутых кристаллах позволяет развить теорию дифракции фемтосекундных импульсов. В частности, теоретически возможна фокусировка этих импульсов.

Список литературы:

1.Бушуев В.А. Дифракция фемтосекундных импульсов излучения рентгеновского лазера на свободных электронах // Материалы Симпозиума «Нанофизика и наноэлектроника-2005». 2005. Нижний Новгород. С. 279–280.

2.Бушуев В.А. Дифракционное отражение от кристалла фемтосекундных импульсов рентгеновского лазера на свободных электронах // Изв. РАН, сер.физ. – 2005. – Т. 69, № 12. – С. 1710–1715.

3.Бушуев В.А. О возможности временной компрессии фемтосекундных импульсов излучения рентгеновского лазера на свободных электронах при брэгговском отражении от кристалла // Материалы Симпозиума «Нанофизика и наноэлектроника-2006». 2006. Нижний Новгород. С. 368–369.

4.Chukhovskii F.N., Förster E. Time-Dependent X-ray Bragg Diffraction // Acta Cryst. (A). – 1995. – Vol. 51. – P. 668–672.

5.Graeff W. Tailoring the time response of a Bragg reflection to shortx-ray pulses // J. Synchr.Rad. – 2004. – Vol. 11, part 3. – P. 261–265.

6.Malgrange C., Graeff W. Diffraction of short X-ray pulses in the general asymmetric Laue case-an analytic treatment // J. Synchr.Rad. – 2003. – Vol. 10, part 3. – P. 248–254.