СИНХРОНИЗАЦИЯ  И  ДЕСИНХРОНИЗАЦИЯ  АВТОМОДУЛЯЦИОННЫХ  КОЛЕБАНИЙ  В  КОЛЬЦЕВОМ  ЧИП-ЛАЗЕРЕ  ПОД  ДЕЙСТВИЕМ  ПЕРИОДИЧЕСКОГО  СИГНАЛА  И  ШУМА

Дудецкий  Вадим  Юрьевич

аспирант  физический  факультет, 
Московского  государственного  университета  имени  М.В.  Ломоносова. 
РФ,  г.  Москва

E-mail: 

SYNCHRONIZATION  AND  DESYNCHRONIZATION  OF  SELF-MODULATION  OSCILLATIONS  IN  A  RING  CHIP  LASER  UNDER  THE  INFLUENCE  OF  A  PERIODIC  SIGNAL  AND  NOISE

Vadim  Dudetskiy

postgraduate  student  department  of  Physics, 
of  Moscow  State  University  M.V.  Lomonosov, 

Russia,  Moscow\

АННОТАЦИЯ

Приведены  результаты  численного  моделирования  и  экспериментальных  исследований  влияния  шума  накачки  на  синхронизацию  автомодуляционных  колебаний  в  твердотельном  кольцевом  лазере  с  периодической  модуляцией  накачки.  Установлено,  что  в  отличие  от  эффекта  десинхронизации,  обычно  возникающего  под  действием  шума  при  синхронизации  автоколебаний  (порядка1/1)  периодическим  сигналом,  синхронизация  порядка  1/2  может  сопровождаться  конструктивным  воздействием  шума.  При  достаточно  малых  интенсивностях  шум  накачки  способствует  синхронизации  автоколебаний,  сужению  их  спектра  и  увеличению  отношения  сигнал/шум.

ABSTRACT

The  result  of  numerical  simulation  and  experimental  studies  of  the  effect  of  pump  noise  n  the  synchronization  automodulation  oscillation  in  solid-state  ring  laser  with  periodic  modulation.  It  is  found  that,  in  contrast  to  the  desynchronization  effect,  usually  occurring  under  the  action  of  noise  on  the  synchronizatiom  of  self-oscillations  (of  the  order  of  1/1)  periodic  signal,  synchronization  of  the  order  of  1/2  may  de  accompanied  by  constructive  effects  of  noise.  At  a  sufficiently  low  intensity  noise  of  the  pump  contributes  to  the  synchronization  of  self-oscillations,  narrowing  their  range  and  increasing  the  signal-to-noise  ratio.

Ключевые  слова:  Твердотельный  кольцевой  лазер;  автомодуляционный  режим  генерации;  синхронизация  частоты;  десинхронизация  частоты;  шум;  спектр;  бистабильность;  стохастический  резонанс.

Keywords:A  solid-state  ring  laser;  automodulation  the  mode  of  generation;  frequency  synchronization;  desynchronization  frequency;  the  noise;  spectrum;  bistability;  stochastic  resonance.

Введение

Синхронизация  колебаний,  возникающих  в  нелинейных  динамических  системах,  является  фундаментальным  явлением,  исследованию  которых  посвящено  ряд  работ  (см,  например,  монографии  [8;  11].  Общий  случай  вынужденной  синхронизации  автоколебаний  порядка  n/m  характеризуется  следующим  соотношением  между  частотой  внешнего  сигнала  w  и  частотой  синхронизованных  колебаний  W_s:  nw  =  mW_s,  где  n  и  m  —  целые  числа.

В  работах  [8—11]  исследовано  влияние  шумов  на  синхронизацию  автоколебаний  порядка  1/1.  Под  воздействием  шума,  вследствие  диффузии  фазы  автоколебаний,  происходит  уширение  спектра  синхронизованных  автоколебаний,  и  при  достаточно  сильном  шуме  происходит  десинхронизация. 

Такие  качественные  изменения  были  установлены  теоретически  и  наблюдались  экспериментально  лишь  в  случае  вынужденной  синхронизации  периодических  автоколебаний  порядка  1/1.  В  настоящей  работе  проведены  теоретические  и  экспериментальные  исследования,  в  которых  изучено  влияние  шума  накачки  на  синхронизацию  периодических  автомодуляционных  колебаний  порядка  1/2  в  твердотельном  кольцевом  лазере  (ТКЛ).  Проведенные  исследования  показали,  что  в  определенном  диапазоне  интенсивностей  шума  накачки  стохастическое  воздействие  играет  конструктивную  роль:  шум  способствует  синхронизации  автоколебаний,  сужению  их  спектра  и  увеличению  отношения  сигнал/шум.

Кроме  того,  ранее  синхронизация  автомодуляционных  колебаний  излучения  ТКЛ  исследовалась  теоретически  и  экспериментально  в  условиях,  когда  внешний  сигнал,  вызывающим  синхронизацию,  является  периодическим.  Важное  отличие  исследований,  проведенных  в  представленной  работе,  состоит  в  том,  что  помимо  периодической  модуляции  накачки  осуществлялась  также  и  шумовая  модуляция  с  помощью  генератора  шума,  включенного  в  цепь  питания  лазера  накачки.

Численное  моделирование

При  численном  моделировании  в  настоящей  работе  использовалась  векторная  модель  ТКЛ  [2;  3;  5].

Периодическая  модуляция  накачки  описывается  зависящим  от  времени  превышением  накачки  над  порогом  ,  которое  имеет  вид:  ,  где    —  превышение  накачки  над  порогом  в  отсутствие  модуляции  накачки,    —  глубина  и  частота  модуляции  накачки.  Считаем,  что  шумовая  модуляция  накачки  производится  белым  шумом  и  задана  случайной  функцией  :  ,  где    —  коэффициент  диффузии  (интенсивность)  шума.

Численное  моделирование  проводилось  при  параметрах,  близких  к  экспериментально  измеренным  параметрам  кольцевого  чип-лазера  на  Nd:YAG. 

Время  релаксации  равно  T₁=240  мкс.  Ширина  полосы  резонатора  определялась  по  релаксационной  частоте  .  В  исследуемом  лазере  при  =0.2  основная  релаксационная  частота  равнялась  =  98,5  кГц,  что  дает  величину  w_с/Q  =4.37*10⁸с^-1.  Значение  поляризационного  параметра  =0,75  было  найдено  (так  же,  как  и  в  [3])  по  экспериментально  измеренной  зависимости  дополнительной  релаксационной  частоты  w_r1  от  частотной  невзаимности  резонатора  .

При  численном  моделировании  были  выбраны  следующие  значения  модулей  коэффициентов  связи:  ,  . 

При  этих  значениях  коэффициентов  связи,  частота  автомодуляционных  колебаний  и  отношение  средних  значений  интенсивностей  встречных  волн  близки  к  экспериментально  измеренным  значениям. 

Разность  фаз  комплексных  коэффициентов  связи    трудно  оценить  по  характеристикам  автомодуляционных  колебаний.  Для  простоты,  разность  фаз  коэффициентов  связи    полагалась  равной  нулю.  Предполагалось  также,  что  частотная  и  амплитудная  невзаимности  кольцевого  резонатора  отсутствуют  (W=0  ,  ).

Параметры  исследуемого  двунаправленного  чип–лазера  были  выбраны  таким  образом,  что  в  отсутствие  шумовой  модуляции  накачки  чип–лазер  работал  в  автомодуляционном  режиме  первого  рода. 

В  спектре  мощности  лазера,  работающего  в  этом  режиме,  имеется  один  пик  на  частоте  автомодуляции  ƒ_m. 

В  проведенных  ранее  исследованиях  [1;  4;  6;  12]  по  синхронизации  автомодуляционных  колебаний  рассматривалась  синхронизация,  возникающая  при  частотах  модуляции  накачки,,  близких  к  частоте  автомодуляционных  колебаний  ƒ_m  (синхронизация  порядка  1/1).

В  настоящей  работе  исследована  синхронизация  автомодуляционных  колебаний  при  частотах  модуляции  ƒ_p,  близких  к  2ƒ_m  (синхронизация  порядка  1/2). 

В  этом  случае  при  малой  глубине  модуляции  накачки  h  отсутствует  субгармоника  ƒ_p/2,  на  которой  мог  бы  возникнуть  захват  частоты  автомодуляции  внешним  сигналом  (ƒ_m  =  ƒ_p/2).  С  увеличением  h  может  произойти  параметрическая  раскачка  субгармоники  и  при  ,  где    —  граница  области  синхронизации,  частота  автомодуляционных  колебаний  захватывается  субгармоникой  . 

После  того,  как  возникла  синхронизация,  она  будет  сохраняться  и  при  плавном  уменьшении  h  вплоть  до  второй  границы  области  синхронизации  .  В  области  между  двумя  этими  границами  ()  имеет  место  бистабильность. 

Границы  области  синхронизации  порядка  1/2,  найденные  путем  численного  моделирования  при=  0.15,  показаны  на  рис.  1. 

В  этом  случае,  при  отсутствии  модуляции  накачки,  частота  автомодуляционных  колебаний  равнялась  =  208,5  кГц. 

Отметим,  что  ширина  области  синхронизации  порядка  1/2  значительно  уже  (на  порядок  и  более),  чем  в  случае  синхронизации  порядка  1/1  (см.  для  сравнения  [1;  4;  6;  12]).

Рисунок  1.  Границы    области  синхронизации  порядка  1/2  при  воздействии  на  чип-лазер  периодического  сигнала  модуляции  накачки  с  частотами  ,  близкими  к  удвоенной  автомодуляционной  частоте 

Рассмотрим  влияние  шума  на  синхронизацию  автомодуляционных  колебаний  порядка  1/2.  На  рис.  2,  а  пунктирной  кривой  показан  спектр  интенсивности  автомодуляционных  колебаний  в  отсутствие  шумовой  модуляции  накачки. 

В  этом  случае  имела  место  периодическая  модуляция  накачки  на  частоте  =  414  кГц  с  глубиной  модуляции  =  0.15,  однако  (поскольку  )  синхронизация  порядка  1/2  не  возникала,  и  частота  автомодуляционных  колебаний  оставалась  такой  же,  как  и  при  отсутствии  периодической  модуляции  (=  208,5  кГц). 

Сплошной  линией  на  рис.  2,  а  показан  спектр,  наблюдаемый  при  наличии  шума  накачки  с  интенсивностью  (коэффициентом  диффузии)  . 

В  относительных  единицах,  которые  используются  далее  для  сравнения  с  экспериментом,  интенсивность  шума  оказывается  равной  =  0.1. 

Под  действием  шума  происходит  переход  в  режим  синхронизации  порядка  1/2,  частота  автомодуляционных  колебаний  захватывается  субгармоникой  периодического  сигнала  модуляции  накачки  =  207  кГц.

Спектр,  показанный  на  рис.  2,  а,  характерен  для  случая  шума  с  достаточно  малой  интенсивностью,  0,5.  С  увеличением  интенсивности  шума  возрастает  диффузия  фазы  автомодуляционных  колебаний  и  происходит  их  десинхронизация  (см.  рис.  2,  б,  в).

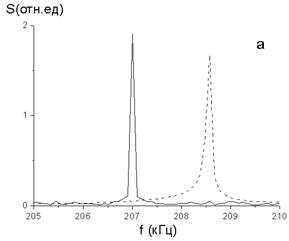
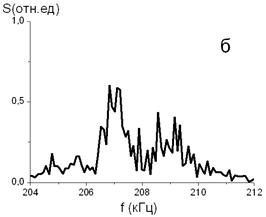
Рисунок  2.  Спектры  интенсивности  автомодуляционных  колебаний  при  периодической  модуляции  накачки  с  частотой  =  414  кГц  и  глубиной  модуляции  =  0.15:  (а)  при  отсутствии  шума  (пунктир)  и  при  наличии  шума  с  интенсивностью  (сплошная  линия);  (б)  при  интенсивности  шума  ;  (в)  при  интенсивности  шума 

На  рис.  3  показана  зависимость  отношения  сигнал/шум  для  синхронизации  порядка  1/2  (при  частоте  модуляции  накачки=  412  кГц)  от  интенсивности  шума  D,  найденная  при  численном  моделировании  в  случае  =  0.3,  =  0.15. 

Для  вычисления  отношения  S/N  проводилось  усреднение  по  150  реализациям. 

Как  видно  из  этого  рисунка,  синхронизация  порядка  1/2  возникает  скачком,  начиная  с  некоторого  порогового  значения  интенсивности  шума  D.

Рисунок  3.  Зависимость  отношения  сигнал/шум  при  синхронизации  порядка  1/2  от  интенсивности  шума  D  (частота  модуляции  накачки  =  412  кГц,=  0.3,  =  0.15)

С  увеличением  интенсивности  шума  отношение  сигнал/шум  изменяется  так  же,  как  в  случае  стохастического  резонанса  [7;  13]:  оно  растет  при  малых  интенсивностях  и  уменьшается  при  больших.

 Эксперимент

Экспериментальные  исследования,  как  и  в  случае  численного  моделирования,  проводились  на  ТКЛ,  работающем  в  автомодуляционном  режиме  первого  рода.  При  этом  интенсивности  встречных  волн  совершают  противофазные  гармонические  колебания. 

Спектры  интенсивности  излучения  для  встречных  волн  в  таком  режиме  оказываются  идентичными,  по  этой  причине  ниже  приводятся  лишь  спектры  для  одной  из  волн.

На  рис.  4,  а  приведен  спектр  интенсивности  одной  из  волн  в  окрестности  частоты  автомодуляционных  колебаний  в  отсутствие  шумовой  модуляции  накачки  (D=0,  h=0,27,  ƒ_p/2  =  420  кГц),  показывающий,  что  частота  автомодуляционных  колебаний  в  исследуемом  чип-лазере  оказывается  нестабильной  и  флуктуирует;  ширина  спектра  около  5  кГц.

В  этом  случае  синхронизация  автоколебаний  не  происходит. 

В  режиме  синхронизации  порядка  1/2  (рис.  4,  б,  4,  в),  возникающем  при  добавлении  шума  к  периодической  модуляции  накачки,  в  спектре  интенсивности  излучения  появляется  узкий  пик  на  субгармонике  периодического  сигнала  модуляции  (ƒ_p/2  =  210  кГц).  С  увеличением  интенсивности  шума  интенсивность  этого  пика  сначала  растет,  а  затем  происходит  десинхронизация,  и  пик  на  субгармонике  периодического  сигнала  уширяется  и  исчезает.

Сравнение  экспериментально  измеренных  спектров  (рис.  4)  с  рассчитанными  при  численном  моделировании  (рис.  2)  позволяет  сделать  вывод  о  конструктивной  роли  шума  накачки,  которая  проявляется  в  стохастическом  возбуждении  синхронизации  автоколебаний  порядка  1/2  при  достаточно  малых  интенсивностях  шума.  В  области  достаточно  больших  интенсивностей  шума  возникает  десинхронизация. 

Различие  между  спектрами,  полученными  в  эксперименте  и  при  численном  моделировании,  вызвано  тем  обстоятельством,  что  в  эксперименте  (даже  при  отсутствии  внешнего  шума,  создаваемого  генератором)  имеются  значительные  шумы,  приводящие  к  флуктуациям  частоты  автомодуляционных  колебаний  и  уширению  их  спектра. 

При  численном  моделировании  в  отсутствие  шумовой  модуляции  такие  флуктуации  отсутствуют,  и  спектр  автомодуляционных  колебаний  значительно  уже.

Рисунок  4.  Спектры  интенсивности  одной  из  волн  в  окрестности  частоты  автомодуляционных  колебаний  при  периодической  модуляции  накачки  с  частотой  =  420  кГц  и  глубиной  модуляции  :  (a)  в  отсутствие  шумовой  модуляции  накачки  ()  и  при  наличии  шумовой  модуляции(б),  (в),  (г)

Выводы

Исследовано  влияние  шума  на  синхронизацию  порядка  1/2  автомодуляционных  колебаний  излучения  ТКЛ  периодическим  сигналом,  модулирующим  мощность  излучения  накачки. 

Установлено,  что  при  малых  интенсивностях  шумовой  модуляции  накачки  шум  способствует  вынужденной  синхронизации  автоколебаний  периодическим  сигналом:  в  отсутствие  внешнего  шума  синхронизация  может  отсутствовать,  а  при  добавлении  достаточно  слабого  шума  происходит  стохастическое  возбуждение  синхронизации  порядка  1/2.  При  последующем  увеличении  интенсивности  шума  синхронизация  постепенно  пропадает.

При  вынужденной  синхронизации  автомодуляционных  колебаний  порядка  1/2  имеет  место  бистабильность.

Если  синхронизация  еще  не  возникла,  имеет  место  квазипериодический  режим,  в  котором  основными  спектральными  компонентами  являются  частота  колебаний  и  частота  модуляции  накачки. 

Если  переход  в  режим  синхронизации  происходит  из  квазипериодического  режима,  то  для  возникновения  синхронизации  требуется  достаточно  большая  амплитуда  модуляции  накачки. 

Если  же  идти  в  обратном  направлении  из  режима  синхронизации  и  уменьшать  глубину  модуляции  накачки,  то  синхронизация  порядка  1/2  будет  наблюдаться  при  меньших  амплитудах  (при  h2<h<h1). 

Таким  образом,  между  границами  h1  и  h2  существует  область  гистерезиса,  в  котором  существует  как  квазипериодический  режим,  так  и  режим  синхронизации.  Найдена  область,  в  которой  наблюдается  бистабильность.

Зависимость  отношения  сигнал/шум  в  процессе  синхронизации  автомодуляционных  колебаний  от  интенсивности  шума  имеет  вид,  характерный  для  стохастического  резонанса,  т.е.  при  синхронизации  автоколебаний  под  действием  шума  возникает  стохастический  резонанс.

Список  литературы:

1. Аулова  Т.В.,  Кравцов  Н.В.,  Ларионцев  Е.Г.,  Чекина  С.Н.  Квазипериодический  режим  автомодуляционных  колебаний  с  низкочастотной  импульсной  огибающей.  —  Квантовая  электроника,  41,  13  (2011).
2. Бойко  Д.Д.,  Кравцов  Н.В.  Влияние  поляризационных  свойств  резонатора  на  зависимость  частоты  автомодуляции  от  параметров  чип-лазера.  —  Квантовая  электроника,  25,  880  (1998).
3. Золотоверх  И.И.,  Кравцов  Н.В.,  Ларионцев  Е.Г.,  Фирсов  В.В.,  Чекина  С.Н.  Влияние  различия  поляризаций  встречных  волн  на  динамику  твердотельных  кольцевых  лазеров.  —  Квантовая  электроника,  37,  1011  (2007).
4. Золотоверх  И.И.,  Клименко  Д.Н.,  Кравцов  Н.В.,  Ларионцев  Е.Г.  Влияние  периодической  модуляции  потерь  на  динамику  автомодуляционных  колебаний  в  твердотельном  кольцевом  лазере.  —  Квантовая  электроника,  23,  №  7,  625  (1996).
5. Кравцов  Н.В.,  Ларионцев  Е.Г.  Нелинейная  динамика  твердотельных  кольцевых  лазеров.  —  Квантовая  Электроника,  36,  №  3,  (2006).
6. Кравцов  Н.В.,  Пашинин  П.П.,  Сидоров  С.С.  Захват  частот  автомодуляционных  колебаний  и  гистерезис  неавтономного  двунаправленного  кольцевого  твердотельного  лазера.  —  Квантовая  электроника,  32,  562  (2002).
7. Кравцов  Н.В.,  Ларионцев  Е.Г.,  Чекина  С.Н.  Стохастический  резонанс  на  субгармонике  периодического  сигнала  модуляции  в  твердотельном  лазере.  —  Квантовая  электроника,  43,  917  (2013).
8. Пиковский  А.,  Розенблюм  М.,  Куртс  Ю.  Синхронизация:  фундаментальное  нелинейное  явление  (М.  Техносфера,  2003).
9. Стратонович  Р.Л.  Избранные  вопросы  теории  флуктуаций  в  радиотехнике.  —  М.:  Сов.  Радио,  1961.
10. Стратонович  Р.Л.  Случайные  процессы  в  динамических  системах.  М.  —  Ижевск:  Институт  компьютерных  исследований,  НИЦ  «Регулярная  и  хаотическая  динамика»,  2009.
11. Balanov  A.,  Janson  N.,  Postnov  D.,  Sosnovtseva  O.  Synchronization^  From  Simple  to  Complex.  /  Berlin:  Springer,  2009.
12. Kravtsov  N.V,  Lariontsev  E.G.,  Pashinin  P.P.,  Sidorov  S.S.,  Firsov  V.V.  Frequency  Locking  of  Self-Modulation  Oscillations  in  a  Ring  Laser  by  an  External  Signal.  Laser  Phys.,  13,  305  (2003).
13. Jung  P.,  Hanggi  P.  Amplification  of  Small  Signals  via  Stochastic  Resonance.  Phys.  Rev.  A,  44,  8032  (1991).