БИФУРКАЦИИ  ТРАНСЗВУКОВОГО  ТЕЧЕНИЯ  В  МОДЕЛИ  ВОЗДУХОЗАБОРНИКА

Кузьмин  Александр  Григорьевич

д-р  физ.-мат.  наук,

С-Петербургский  государственный  университет

РФ,  г.  Санкт-Петербург

E-mail:  

Матюхина  Ирина  Анатольевна

программист 
Крыловского  государственного  научного  центра,

РФ,  г.  Санкт-Петербург

E -mail:  imatyuhina@inbox.ru

TRANSONIC  FLOW  BIFURCATION  IN  AN  INTAKE  MODEL

Alexander  Kuzmin

Dr.Sc., 
St.  Petersburg  State  University, 
Russia,  St.  Petersburg

Irina  Matyukhina

programmer, 
Krylov  State  Research  Center, 
Russia,  St.  Petersburg

Данная  работа  выполнена  при  поддержке  РФФИ  (проект  №  13-08-00288)  с  использованием  ресурсов  вычислительного  центра  СПбГУ  ( http://cc.spbu.ru).

АННОТАЦИЯ

Численно  исследовано  двумерное  турбулентное  течение  воздуха  в  сужающемся-расширяющемся  канале  с  плоской  верхней  стенкой.  Рассмотрены  режимы  течения  со  сверхзвуковой  скоростью  в  свободном  потоке  и  в  расширяющейся  части  канала.  Решения  нестационарных  уравнений  Навье-Стокса,  осредненных  по  Рейнольдсу,  получены  с  помощью  вычислительной  программы  ANSYS  CFX-15,  основанной  на  методе  конечных  объемов.  Показано  наличие  существенного  гистерезиса  зависимости  положения  ударной  волны  от  числа  Маха  натекающего  потока  и  наклона  верхней  стенки  канала.  Изучено  влияние  кривизны  нижней  стенки  на  ширину  гистерезиса.

ABSTRACT

The  2D  turbulent  airflow  in  a  convergent-divergent  channel  with  a  flat  upper  wall  is  studied  numerically.  Flow  regimes  in  which  the  velocity  is  supersonic  in  the  free  stream  and  divergent  part  of  the  channel  are  examined.  Solutions  of  the  unsteady  Reynolds-averaged  Navier-Stokes  equations  are  obtained  with  a  finite-volume  solver  ANSYS  CFX-15.  Computations  reveal  a  considerable  hysteresis  in  a  dependence  of  the  shock  wave  position  on  the  free-stream  Mach  number  and  the  upper  wall  inclination.  An  effect  of  the  lower  wall  curvature  on  the  hysteresis  width  is  studied. 

Ключевые  слова:  ударная  волна;  сверхзвуковой  поток;  торможение;  неустойчивость.

Keywords:  shock  wave;  supersonic  flow;  deceleration;  instability.

Введение.  Актуальность  исследований  устойчивости  течений  в  воздухозаборниках  обусловлена  необходимостью  повышения  эффективности  работы  воздушно-реактивных  двигателей.  Канал  сверхзвукового  воздухозаборника  состоит  из  сужающейся  части,  расположенной  выше  по  течению  от  минимального  сечения  (горла),  и  расширяющейся  части  ниже  по  течению.  На  расчетном  режиме  работы  воздухозаборника  смешанного  сжатия  происходит  формирование  косых  скачков  уплотнения  в  сужающейся  части  канала  и  замыкающего  скачка  сразу  за  минимальным  сечением.  Однако  такая  система  ударных  волн  оказывается  весьма  чувствительной  к  изменениям  числа  Маха  натекающего  потока  M_∞  и  угла  атаки.  В  частности,  при  меньших  значениях  M_∞  по  сравнению  с  расчетным  значением  происходит  выбивание  системы  ударных  волн  и  их  слияние  в  один  скачок,  расположенный  перед  входом  в  канал.  При  этом  в  расширяющейся  части  воздухозаборника,  как  правило,  устанавливается  дозвуковая  скорость  течения. 

В  данной  работе  исследуются  режимы  со  сверхзвуковой  скоростью  в  расширяющейся  части  как  в  случае  положения  косого  скачка  внутри  канала,  так  и  при  его  выбивании.  Близкие  режимы  изучались  в  работах  [1;  2]  для  изогнутых  каналов  и  в  [3]  для  ударной  волны,  отошедшей  от  цилиндра,  расположенного  над  стенкой  с  угловой  точкой. 

Постановка  задачи.  Рассмотрим  плоский  канал,  нижняя  стенка  которого  имеет  длину  1,5  и  излом  16°  при  x=1  :

  y =0  при  0≤  x  ≤  1  ,  y=  −(x−1)  tan16°  при  1<x≤  1,5  .  (1)

Здесь  и  далее  все  линейные  величины  измеряются  в  метрах.  Наряду  с  профилем  (1)  будем  рассматривать  профили  со  сглаживанием  излома  дугой  окружности  радиуса  R.  При  R=1,42307  прямолинейный  участок  стенки  переходит  в  окружность  в  точке  x=0,9,  а  при  R=  2,84615  −  в  точке  x=0,7. 

Профилем  верхней  стенки  канала  является  прямоугольник  толщиной  0,02  с  внутренней  стороной  y=1-(x-0,4)tgθ,  где  0,4  ≤x≤  2.  Угол  наклона  θ  стенки  к  оси  x,  отсчитываемый  по  часовой  стрелке,  изменяется  в  пределах  от  0  до  11°.  Верхней  границей  расчетной  области  является  отрезок  y=5,  0≤x≤2,  который  расположен  на  достаточном  удалении  от  верхней  стенки  для  исключения  его  влияния  на  течение  в  канале.  Входной  границей  является  отрезок  x=0,  0≤y≤5.  С  целью  экономии  вычислительных  ресурсов  в  качестве  выходной  границы  Γ,  расположенной  вне  канала,  вместо  вертикального  отрезка  x=2  выбран  наклонный  отрезок,  соединяющий  угловую  точку  x=2,  y=5  и  точку  с  абсциссой  x=0,7,  находящуюся  на  внешней  стороне  верхней  стенки. 

На  входной  границе  задана  продольная  компонента  скорости  потока  U_∞  ,  нулевое  значение  вертикальной  и  поперечной  компонент  скорости,  статическое  давление  p_∞=50000  н/м²  и  статическая  температура  T_∞=250  K,  которой  соответствует  скорость  звука  a_∞=317,02  м/с  при  показателе  адиабаты  1,4.  На  границе  Γ  и  на  выходе  из  канала  ставится  условие  сверхзвуковой  скорости  течения,  а  на  стенках  —  условие  прилипания  и  отсутствие  теплового  потока.  В  качестве  начальных  данных  в  расчетной  области  использовались  параметры  натекающего  потока  или  поле  течения,  полученное  для  некоторого  предыдущего  значения  M_∞  =  U_∞  /a_∞  .

Численные  решения  системы  уравнений  Навье-Стокса  находились  с  помощью  вычислительной  программы  ANSYS  CFX-15  второго  порядка  точности  на  неструктурированных  сетках  с  числом  ячеек  около  1,5´10⁵.  Использовалась  модель  турбулентности  k-ω  SST  и  глобальные  шаги  по  времени  для  нахождения  установившегося  течения.  Тестирование  программы  проводилось,  в  частности,  на  задаче  трансзвукового  течения  газа  в  канале  с  круговым  выступом  на  верхней  стенке  [2]. 

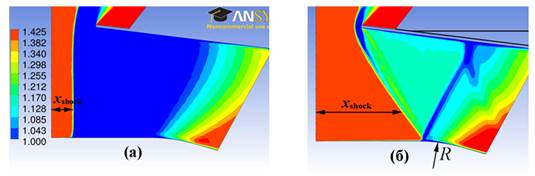
Рисунок  1.  Изомахи  при  угле  наклона  верхней  стенки  θ=7°  и  радиусе  скругления  излома  нижней  стенки  R =1,42307.  Разные  картины  течения  получены  при:  a)  увеличении  M_∞  до  1,425  ,  б)  уменьшении  M_∞  до  1,425

Результаты  расчетов.  Было  проведено  исследование  положения  ударной  волны  в  канале  с  изломом  нижней  стенки,  а  также  при  двух  радиусах  его  скругления,  в  диапазоне  числа  Маха  M_∞  от  1,36  до  1,60. 

В  качестве  параметра,  характеризующего  положение  ударной  волны  в  канале,  использовалась  координата  x_shock  точки  пересечения  ударной  волны  с  горизонталью  y=0,25  м.  Расчеты  установившегося  течения  при  M_∞=1,40  и  R=1,42307  показали,  что  отошедшая  от  верхней  стенки  ударная  волна  расположена  перед  входом  в  канал.  С  увеличением  M_∞  до  1,425  расстояние  от  ударной  волны  до  входа  незначительно  уменьшается,  см.  рис.  1а.  При  возрастании  M_∞  до  1,512  происходит  дальнейшее  постепенное  смещение  ударной  волны  вниз  по  потоку  и  увеличение  координаты  x_shock  (см.  нижнюю  ветвь  графика  2  на  рис.  2).  Последующее  увеличение  M_∞  до  1,514  приводит  к  резкому  перемещению  ударной  волны  к  горлу  канала  и  скачкообразному  изменению  x_shock  от  0,422  до  0,885. 

С  уменьшением  M_∞  от  1,514  до  1,425  полученная  картина  течения  с  наклонной  ударной  волной,  достигающей  окрестности  горла,  сохраняется.  При  этом  точка  отражения  ударной  волны  от  нижней  стенки  смещается  вверх  по  течению,  и  происходит  постепенное  формирование  маховского  отражения,  см.  рис.  1б.  При  M_∞=1,41  маховская  конфигурация  с  тройной  точкой  становится  наиболее  ярко  выраженной.  Дальнейшее  уменьшение  M_∞  приводит  к  расщеплению  сверхзвуковой  области  на  две  части  и  выбиванию  ударной  волны  из  канала  при  сохранении  сверхзвуковой  скорости  в  его  расширяющейся  части. 

Сравнение  графиков  1—3  на  рис.  2  показывает,  что  с  увеличением  радиуса  скругления  излома  R  от  0  до  2,84615  ширина  гистерезиса  по  числу  Маха  уменьшается  вдвое. 

Расчеты  поля  течения  для  большего  радиуса  R=4,26922  (при  котором  прямолинейный  участок  нижней  стенки  переходит  в  дугу  окружности  в  точке  x=0,5)  показали  возможность  реализации  режимов  с  косым  скачком,  достигающим  горла,  в  диапазоне  M_∞≥1,395.  График  зависимости  x_shock(M_∞)  при  этом  расположен  весьма  близко  к  верхней  ветви  графика  3  на  рис.  2.  Однако  уменьшение  числа  Маха  до  значений  M_∞<1,395  приводит  к  выбиванию  скачка  с  установлением  дозвуковой  скорости  течения  во  всем  канале. 

На  рис.  3  представлены  графики,  иллюстрирующие  зависимость  положения  ударной  волны  от  угла  наклона  верхней  стенки  θ  при  фиксированных  значениях  M_∞.  Ширина  гистерезиса  по  углу  θ  в  обоих  случаях  составляет  около  3°. 

Рисунок  2.  Зависимость  координаты  x_shock   ударной  волны  от  M_∞  при  θ=7°  :  1  —  для  нижней  стенки  с  изломом  (1),  2  —  скругление  излома  дугой  радиуса  R=1,42307,  3  —  скругление  дугой  радиуса  R=  2,84615.

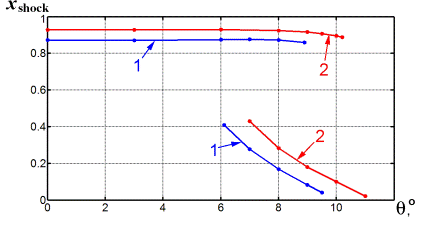
Рисунок  3.  Зависимость  координаты  x_shock   ударной  волны  от  угла  наклона  верхней  стенки  θ  для  канала  с  изломом  (1):  1  —  M_∞  =  1,52,  2  —  M_∞  =  1,58  .

Список  литературы:

1.Кузьмин  А.,  Матюхина  И.  Бифуркации  турбулентного  течения  в  канале  при  взаимодействии  сверхзвуковых  зон  //  Технические  науки  —  от  теории  к  практике  /  Сб.  ст.  по  материалам  XXXVIII  междунар.  науч.-практ.  конф.  —  2014  —  9  (34).  Новосибирск:  Изд.  «СибАК»,  —  с.  79—84. 

2.Kuzmin  A.  Shock  wave  instability  in  a  channel  with  an  expansion  corner  //  International  Journal  of  Applied  Mechanics.  —  2015  —  Vol.  7,  —  №  2,  —  pp.  1—9.

3.Kuzmin  A.  Instability  of  the  shock  wave/  sonic  line  interaction  //  Centre  pour  la  Communication  Scientifique  Directe.  France.  —  2015  —  №  hal-01136894,  —  pp.  1—11,  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://hal.archives-ouvertes.fr/hal-01136894/