АДАПТИВНОЕ  ПРОГНОЗИРОВАНИЕ  ДЛЯ  ПРОЦЕССА  АВТОРЕГРЕССИИ  СО  СЛУЧАЙНЫМ  ПАРАМЕТРОМ

Кусаинов  Марат  Исламбекович

аспирант 
Томского  Государственного  Университета, 
РФ,  г.  Томск

E-mail: 

ADAPTIVE  PREDICTION  FOR  RANDOM  COEFFICIENT  AUTOREGRESSIVE  PROCESS

Marat  Kusainov

postgraduate  student, 
Tomsk  State  University, 
Russia,  Tomsk

АННОТАЦИЯ

Решается  задача  адаптивного  прогнозирования  значений  устойчивого  многомерного  процесса  авторегрессии  первого  порядка  с  дрейфом  параметра  динамики.  С  использованием  метода  усечённого  оценивания  неизвестных  параметров  построены  одношаговые  прогнозы  значений  процесса.  Для  заданной  функции  потерь  решена  задача  оптимизации,  показана  асимптотическая  оптимальность  процедуры  прогнозирования,  для  чего  вводится  специальный  момент  остановки.

ABSTRACT

The  problem  of  adaptive  prediction  for  stable  multivariate  autoregressive  process  of  the  first  order  with  parameter  drift  is  studied.  A  one-step  adaptive  predictor  of  the  process’  values  is  built  using  the  truncated  estimation  method  to  estimate  unknown  parameters.  For  a  certain  loss  function  the  optimization  is  performed,  the  asymptotic  optimality  of  the  prediction  procedure  is  shown,  a  special  stopping  time  is  introduced  to  this  end.

Ключевые  слова :  процесс  авторегрессии;  одношаговые  прогнозы;  метод  усечённого  оценивания.

Keywords :  autoregressive  process;  one-step  predictor;  truncated  estimation  method.

Постановка  задачи

    Пусть  устойчивый  многомерный  процесс  авторегрессии  задаётся  следующим  уравнением

    (1)

где

Λ  —  это  неизвестная    матрица,  последовательности      независимы  между  собой  и  образованы  из  независимых  одинаково  распределенных  случайных  векторов  с  нулевым  средним  и  конечной  дисперсией    Устойчивость  процесса  требует  также  выполнения  условия    и  того,  чтобы  матрица    где    —  кронекеровское  произведение  матриц  Y  и  Z,  была  устойчива.  Такая  модель  описывает  специфику  многих  стохастических  процессов  лучше  авторегрессии  с  постоянными  параметрами  динамики.

    Хорошо  известно,  что  оптимальным  в  среднеквадратическом  смысле  одношаговым  прогнозом  является  условное  математическое  ожидание  относительно  «прошлого»  процесса,  т.  е.

Заменяя  неизвестную  матрицу  Λ  некоторой  оценкой    получим  адаптивные  прогнозы  вида

Тогда  соответствующая  ошибка  прогноза

(2)

Обозначим    выборочное  среднее  квадратов  нормы  ошибок  прогноза

Определим  функцию  потерь

Параметр    можно  трактовать  как  стоимость  ошибки  прогнозов. 

    По  определению  соответствующая  функция  риска  имеет  вид

где    обозначает  математическое  ожидание  по  распределению    при  заданном  значении  вектора  параметров  .  Обозначим  Θ  множество  векторов,  такое  что  для  матрица    устойчива  и 

    Основная  задача  заключается  в  минимизации    по  размеру  выборки  n.  Схожая  задача  для  скалярного  процесса  авторегрессии  без  дрейфа  решалась  в  работе  [3],  где  для  оценивания  Λ  был  использован  метод  наименьших  квадратов,  для  многомерного  процесса  авторегрессии  без  дрейфа  —  в  работе  [2].

Основной  результат

    Для  оценивания  Λ  используется  метод  усечённого  оценивания,  предложенный  В.А.  Васильевым  в  работе  [4]  и  позволяющий  получить  оценку  параметра  с  гарантированной  точностью  в  среднеквадратическом  смысле  при  фиксированном  объёме  наблюдений. 

    Усечённая  оценка  матрицы    основывается  на  оценке  по  методу  наименьших  квадратов

и  определяется  следующим  образом

Здесь  ,    а  χ(B)  обозначает  индикатор  множества  B.

    Для  выделения  главной  части  риска    перепишем  величину    используя  определение  (2)  и  независимость  шумов

Заметим,  что    где  tr(Y)  обозначает  след  матрицы  Y,  аргумент  времени  (k)  опущен  для  простоты  записи.  Используя  свойства  следа,  получим    где    не  зависит  от  времени  в  силу  свойств  η(k).  Тогда  риск  принимает  вид

  (3)

где

Матрица  F  существует  и  положительно  определена  при    [1].

    Оценим  первое  слагаемое  D_n.  Используя  определение  x(k),  запишем

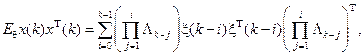
пренебрегая  незначимым  слагаемым  с  x(0).  Воспользуемся  оператором    обращающим    матрицу  Y  в    вектор,  составленный  из  столбцов  Y.  Согласно  свойству  оператора    имеем

  (4)

где      Поскольку    имеем 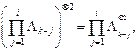   а  следовательно  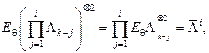  вследствие  независимости  η(k).  Тогда  ряд  в  (4)  приобретает  вид  суммы  первых  k  членов  многомерной  геометрической  прогрессии,  и  с  учётом  устойчивости 

откуда    Используя  это  представление,  нетрудно  показать,  что

здесь  и  далее  C  обозначает  неотрицательные,  необязательно  равные  между  собой  постоянные,  значения  которых  не  принципиальны. 

    Для  оценивания  второго  слагаемого  D_n  используем  свойства  оценки    для  установления  которых  ниже  сформулирована  лемма.  Определим  вспомогательную  величину    где    —  целая  часть    и 

    Лемма  1.   Пусть  (1)  задаёт  процесс  x(k),  и  для  некоторого  целого    выполняются  условия

Предположим  также,  что  матрица    устойчива.  Тогда  для  усечённой  оценки    справедливо

(i) для    

(ii)   для    

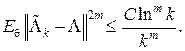  (5)

Доказательство  Леммы  1  проводится  аналогично  [2].

    Используя  (5)  и  неравенство  Коши-Буняковского,  получим

Таким  образом,  использование  оценки    в  прогнозе  гарантирует

Обозначим  Принимая  во  внимание  определение  (3),  поставленная  задача  сводится  к  минимизации  главной  части  функции  риска

Нетрудно  видеть,  что  минимум  достигается  на  значении 

  (6)

Тогда  приблизительное  минимальное  значение  риска

Подобно  [2],  [3],  введём  момент  остановки  T_A,  приближающий  установленный  теоретически    вида  (6),  заменяя  неизвестный  параметр    некоторой  его  оценкой    

  (7)

где:  n_A  —  так  называемая  задержка  процедуры,  зависящая  от  значения  A,  и

Следующая  теорема  устанавливает  асимптотическую  эквивалентность  T_A  и    в  смысле  сходимостей  почти  наверное  и  в  среднем,  а  также  оптимальность  процедуры  адаптивного  прогнозирования  в  смысле  эквивалентности  величин

и    

    Теорема  1.   Пусть  матрица    устойчива,  ,    и    в  (7)  удовлетворяет    для    Тогда  для  любого 

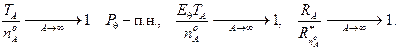
Заключение

В  настоящей  работе  решена  задача  построения  оптимальных  одношаговых  прогнозов  значений  многомерного  устойчивого  процесса  авторегрессии  первого  порядка  с  дрейфом  параметра  динамики.  Все  параметры  модели  полагаются  неизвестными.  Прогнозы  построены  на  базе  оценок  по  методу  усечённого  оценивания,  достигающего  заданной  точности  на  выборках  конечного  объёма.  Оптимальный  объём  наблюдения  определён  как  теоретически,  так  и  на  основе  данных  в  виде  момента  остановки,  показана  их  асимптотическая  эквивалентность  в  случае  неограниченно  растущей  цены  ошибки  прогноза.

Список  литературы:

1.Кашковский  Д.В.,  Конев  В.В.  О  последовательных  оценках  параметров  авторегрессии  со  случайными  коэффициентами  //  Автометрия.  —  2005.  —  №  1.  —  С.  70—81.

2.Kusainov  M.I.,  Vasiliev  V.A.  On  optimal  adaptive  prediction  of  multivariate  autoregression  //  Sequential  Analysis.  —  2015.  —  №  2.  —  С.  211—234.

3.Sriram  T.N.  Sequential  estimation  of  the  autoregressive  parameter  in  a  first  order  autoregressive  process  //  Sequential  Analysis.  —  1988.  —  №  7.  —  С.  53—74.

4.Vasiliev  V.A.  Truncated  estimation  method  with  guaranteed  accuracy  //  Annals  of  Institute  of  Statistical  Mathematics.  —  2014.  —  №  1.  —  С.  141—163.