Статья опубликована в рамках: XXX Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 мая 2015 г.)
Наука: Физика
Секция: Механика жидкости, газа и плазмы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
РАСПРОСТРАНЕНИЕ ПРОПАНА В ПРИЗЕМНОЙ ПОВЕРХНОСТИ ОТ ПОСТОЯННОГО ИСТОЧНИКА
Хамидуллин Ильдар Раифович
канд. физ.-мат. наук, доцент кафедры математического моделирования и информационной безопасности Нефтекамского филиала федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Башкирский государственный университет», РФ, г. Нефтекамск
DISTRIBUTION OF PROPANE IN THE GROUND SURFACE OF A CONTINUOUS SOURCE
Ildar Khamidullin
candidate of physical and mathematical sciences, assistant professor of mathematical modeling and information security department of Neftekamsk branch of Bashkir State University, Russia, Neftekamsk
АННОТАЦИЯ
В работе представлены результаты численных расчетов распространения пропана от постоянного источника выброса. Получены поля концентраций пропана, давлений, температур, скоростей и др. параметров. Анализировано влияние скорости истечения пропана от источника на распространение пропано-воздушной смеси.
ABSTRACT
The results of numerical calculations of propagation propane from a permanent source of emissions. The fields obtained propane concentration, pressure, temperature, velocity, etc. parameters. It analyzes the impact of flow rate of propane from a source to distribute propane-air mixture.
Ключевые слова: пропан; постоянный источник.
Keywords : propane; continuous source.
1. Введение. В последние десятилетия населению земли требуется все больше энергии, в том числе получаемые от экологически чистых топлив — углеводородных соединений (природного газа, метана, пропана и др.). Транспортировка газов для уменьшения удельного объема осуществляется при высоких давлениях. При нарушении герметичности емкостей и трубопроводов возможно возникновение аварийных ситуаций [1; 2]. Проблемы безопасности и защиты населения от возможных последствий таких аварий требуют более глубокого изучения распространения выбросов углеводородных газов.
Моделирование таких процессов путем физических экспериментов является основным способом исследований, но требует больших затрат. Наиболее рациональным методом является численное моделирование динамики выбросов в атмосфере, которое позволяет прогнозировать последствия аварий и, соответственно, разрабатывать меры защиты.
2. Математическая модель. Рассмотрим облако как смесь газов, которая принимается за гомогенную среду с плотностью ![]() , температурой T, давлением p. Пусть
, температурой T, давлением p. Пусть ![]() скорость этой среды, определяемая как среднемассовая скорость составляющих
скорость этой среды, определяемая как среднемассовая скорость составляющих
![]() . (1)
. (1)
Введем среднемассовые концентрации каждой компоненты смеси ![]() . Здесь и в дальнейшем индексы i = 1, 2 будут соответствовать углеводороду, воздуху. Эти значения концентраций удовлетворяют условию
. Здесь и в дальнейшем индексы i = 1, 2 будут соответствовать углеводороду, воздуху. Эти значения концентраций удовлетворяют условию
![]() . (2)
. (2)
Для смеси газов выполняется закон Дальтона, и для определения давления смеси используем уравнение Менделеева-Клапейрона
![]() ,
, 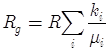 , (3)
, (3)
где: ![]() — универсальная газовая постоянная,
— универсальная газовая постоянная,
![]() — молярные массы газов.
— молярные массы газов.
На основе принятых предположений можем записать систему, описывающую динамику облака газов, в которую входят уравнения неразрывности, диффузии, импульсов для всей смеси и уравнение теплового баланса:
![]() (4)
(4)
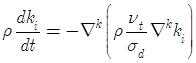 , (5)
, (5)
![]() , (6)
, (6)
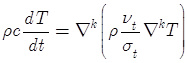 , (7)
, (7)
где ![]() — массовые концентрации компонент смеси. Удельная теплоемкость смеси определяется через удельные теплоемкости компонент
— массовые концентрации компонент смеси. Удельная теплоемкость смеси определяется через удельные теплоемкости компонент
![]() . (8)
. (8)
Для более детального описания процессов тепломассопереноса к данной системе уравнений (3)-(7) добавляются дополнительные уравнения ![]() модели для определения энергии турбулентных пульсаций
модели для определения энергии турбулентных пульсаций ![]() , диссипации
, диссипации ![]() и для коэффициента кинетической турбулентной вязкости
и для коэффициента кинетической турбулентной вязкости ![]()
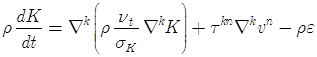 , (9)
, (9)
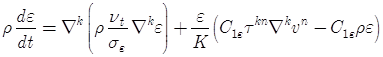 , (10)
, (10)
![]() . (11)
. (11)
Здесь ![]() — турбулентная составляющая тензора касательных напряжений,
— турбулентная составляющая тензора касательных напряжений, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() — эмпирические константы.
— эмпирические константы.
3. Начальные и граничные условия. В начальный момент времени ![]() c температура окружающего воздуха
c температура окружающего воздуха ![]() однородна во всей расчетной области, давление определяется распределением Больцмана. Скорость движения в начальный момент времени равна нулю во всей расчетной области. В облаке горючей смеси в начальный момент времени давление соответствует распределению давления в окружающей атмосфере и температура в облаке
однородна во всей расчетной области, давление определяется распределением Больцмана. Скорость движения в начальный момент времени равна нулю во всей расчетной области. В облаке горючей смеси в начальный момент времени давление соответствует распределению давления в окружающей атмосфере и температура в облаке ![]() однородна и равна температуре окружающего воздуха.
однородна и равна температуре окружающего воздуха.
Начальные значения энергии турбулентных пульсаций ![]() и диссипации энергии
и диссипации энергии ![]() определяются решением задачи о горизонтально однородном воздушном стационарном турбулентном потоке над поверхностью с шероховатостью
определяются решением задачи о горизонтально однородном воздушном стационарном турбулентном потоке над поверхностью с шероховатостью ![]() в виде [3]
в виде [3]
![]() ,
, 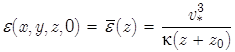 ,
,
где: ![]() = 0,41 — постоянная Кармана,
= 0,41 — постоянная Кармана,
![]() — динамическая скорость.
— динамическая скорость.
Расчетная область ограничена 6 плоскими границами. Верхняя и боковые границы являются открытыми, и на них для параметров задаются фоновые значения. Нижняя граница является закрытой, и на ней скорость равна нулю. Размеры расчетной области выбраны достаточно большими, чтобы за характерные времена горения облака, возмущения отраженные от границ не достигли исследуемой области.
Значения энергии турбулентных пульсаций ![]() и диссипации энергии
и диссипации энергии ![]() на открытых границах равны фоновым значениям, а на нижней границе — ставятся условия непротекания.
на открытых границах равны фоновым значениям, а на нижней границе — ставятся условия непротекания.
4. Численный метод решения. Численная схема решения системы уравнений (3)—(11) основана на методе крупных частиц. К преимуществам данного метода относится устойчивость в широком диапазоне скорости движения среды. Трехмерная постановка задачи позволяет моделировать динамику облака углеводорода при произвольной конфигурации наземных объектов и с учетом рельефа местности.
5. Результаты расчетов. Рассмотрим простейший случай постоянного выброса, когда источник выброса находится на поверхности земли в центре расчетной сетки. Были проведены численные эксперименты с объемным расходом источника 1 м3/с, 5 м3/с, 10 м3/с, 15 м3/с с размером источника 1*1 м2.
Результаты расчетов показали, что облако пропано-воздушной смеси (рис. 1) локализуется в основном над источником выброса. При многократном увеличении объемного расхода источника объем образовавшегося облака растет быстрее, что связано с увеличением площади соприкосновения облака с окружающим воздухом.
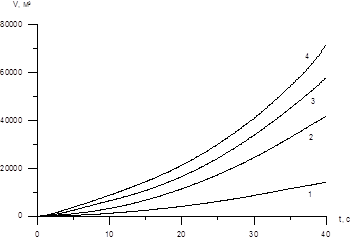
Рисунок 1. Эволюция объема облака при объемном расходе источника:
1 — 1 м3/с, 2 — 5 м3/с, 3 — 10 м3/с, 4 — 15 м3/с.
Зона возможного поражения растет очень быстро. На рисунке 2 указаны случаи объемного расхода объемного источника: 1 м3/с, 5 м3/с в момент времени 10 с после начала истечения пропана. Видно, что пропан расстилается около земной поверхности, т. к. плотность «чистого» пропана выше плотности воздуха. За довольно маленький промежуток времени даже при относительно небольшом объемном расходе источника за 10 секунд образуется взрывоопасная зона высотой ≈5 метров и шириной ≈15 метров, что соответствует по высоте двум этажам жилого дома и ширине почти одного подъезда.
6. Заключение. В данной работе представлены результаты численных исследований распространения пропана через постоянный источник. Показано, что в течение короткого времени образуется довольно большое по объему взрывоопасное пропано-воздушное облако, при возгорании способное нанести большой урон. Это свидетельствует о том, что нужно дальнейшее изучение возгорания получившейся смеси для оценки возможного ущерба.

Рисунок 2. Взрывоопасные зоны после распространения пропана 10 с при объемном расходе источника: сплошная линия — 1 м3/с, штриховая линия — 5 м3/с.
Список литературы:
1.Бесчастнов М.В. Промышленные взрывы. Оценка и предупреждение. М.: Химия, 1991. — 432 с.
2.Маршалл В. Основные опасности химических производств. Пер. с англ. М.: Мир, 1989. — 672 с.
3.Бояршинов М.Г. Модели переноса и рассеяния примесей в растительном массиве. Пермь: ПГТУ, 2000. — 142 с.
дипломов


Оставить комментарий