ИНФОРМАЦИОННЫЕ  ТЕХНОЛОГИИ  ЧИСЛЕННОГО  МОДЕЛИРОВАНИЯ  ТЕЧЕНИЯ  ВЯЗКОЙ  НЕСЖИМАЕМОЙ  ЖИДКОСТИ  В  ДВУСВЯЗНЫХ  ОБЛАСТЯХ

Токанова  Сая  Оразбеккызы

докторант  ВКГТУ  имени  Д.  Серикбаева,  Республика  Казахстан,  г.  Усть-Каменогорск

Е-mail: 

Малгаждаров  Ержан  Амангазынович

канд.  техн.  наук,  доцент  ВКГУ  имени  С.  Аманжолова,  Республика  Казахстан,  г.  Усть-Каменогорск

INFORMATION  TECHNOLOGY  FOR  NUMERICAL  SIMULATION  OF  VISCOUS  INCOMPRESSIBLE  FLOW  IN  BICONNECTED  DOMAINS

Tokanova  Saya

doctoral   student   D.  Serikbayev  East  Kazakhstan  state  technical  university,

Republic  of  Kazakhstan ,  Ust-Kamenogorsk

Malgazhdarov   Yerzhan

candidate  of  engineering  sciences ,

associate  professor  of  S.  Amanzholov  East  Kazakhstan  State  University,  Republic  of  Kazakhstan,  Ust-Kamenogorsk

В  работе  исследуются  численные  методы  решения  уравнений  Навье-Стокса  в  двухсвязных  областях  и  выполнена  в  рамках  Госбюджетного  проекта,  номер  гос.регистрации  №  0112РК02921,  инвентарный  номер  №  0214РК00220 

АННОТАЦИЯ

В  статье  описывается  метод  для  дополнения  численного  моделирования  вязкой  несжимаемой  жидкости  в  сложных  геометрических  областях.  Задача  рассматривается  в  данной  дискретной  двусвязной  области  с  криволинейной  границей.  Сплайн-интерполяция  выполняется  в  криволинейных  границах.  Разработан  курс  монотонно  разностной  схемы  и  алгоритм  численной  реализации  уравнений  Навье-Стокса  для  вязкой  несжимаемой  жидкости.  Численные  результаты  получены  для  различных  количеств  узлов  сетки.

ABSTRACT

In  this  paper,  the  method  of  supplemented  domains  for  the  numerical  simulation  of  viscous  incompressible  flow  in  the  complex  geometrical  domain  is  considered.  The  problem  is  considered  in  a  discrete  defined  biconnected  domain  with  the  curved  boundary.  The  spline  interpolation  of  curved  boundary  is  conducted.  The  Navier-Stokes  equations  for  viscous  incompressible  fluid  are  selected  for  the  numerical  simulation.  A  stable  finite-difference  scheme  and  an  algorithm  of  numerical  implementation  are  developed.  The  numerical  results  are  obtained  with  different  numbers  of  grid  nodes.

Ключевые  слова :  уравнение  Навье-Стокса;  вязкая  несжимаемая  жидкость;  численное  моделирование;  функция  тока;  сплайн-интерполирование;  криволинейная  двусвязная  область

Keywords :  Navier-Stokes  equations;  viscous  incompressible  fluid;  numerical  simulation;  numerical  experiment;  stream  function;  method  of  supplemented  domains;  cube  spline  interpolation;  curvilinear  biconnected  domain.

Введение

Многие  проблемы  гидродинамики,  гидромеханики,  гидравлики,  акустики,  физиологии  кровообращения,  организации  технологических  процессов  в  силу  умеренных  скоростей  перемещения  среды,  а  также  явлении,  наблюдаемые  в  атмосфере  и  океане  можно  изучать  в  рамках  несжимаемой  вязкой  жидкости.

Для  задач  математического  моделирования  гидрофизических  процессов  в  сложных  областях  актуальной  является  проблема  построения  и  практического  использования  вычислительно-эффективных  методов,  базирующихся  на  применении  оптимальных  криволинейных  сеток,  в  том  числе  нерегулярных  и  построение  сходящихся  итерационных  алгоритмов  решения  задач  вычислительной  гидродинамики.  Переход  в  методах  дискретизации  задач  математической  физики,  связанный  с  использованием  вместо  прямоугольных,  сеток  криволинейных,  в  том  числе  нерегулярных  треугольных  сеток,  позволяет  существенно  сократить  количество  расчетных  ячеек  при  заданной  точности  или  значительно  повысить  точность  моделирования  при  данном  количестве  ячеек.

В  настоящее  время  практика  выдвигает  перед  учёными-прикладниками  различного  рода  задачи,  полное  исследование  которых  может  быть  проведено  в  большинстве  случаев  лишь  путём  вычислительного  эксперимента  (ВЭ)  или  с  помощью  тщательно  поставленного  физического  эксперимента.  Однако  представляющие  практический  интерес  явления  и  технологические  процессы  либо  не  поддаются  все  стороннему  физическому  моделированию,  либо  затраты  на  проведение  таких  экспериментов  чрезмерно  велики.  Эффективным  методом  изучения  динамики  однородной  жидкости  является  численное  моделирование,  позволяющее  с  помощью  вычислительных  экспериментов  на  ЭВМ  анализировать  течения  в  широком  диапазоне  изменений  основных  параметров.

Вопросы  численного  моделирования  уравнений  Навье-Стокса  несжимаемой  жидкости  в  последние  годы  привлекли  к  себе  значительное  внимание  математиков  и  механиков.  Нелинейность  этих  уравнений,  их  пространственно-эллиптический  характер  создают  серьезные  трудности  при  разработке  эффективных  разностных  схем.  Наличие  малого  параметра  при  старших  производных  требует  обеспечения  высокой  степени  точности  решения  уравнений  переноса.

Разработка  эффективных  численных  методов,  и  расчёт  с  их  использованием  существенно  нелинейных  течений  несжимаемой  жидкости  являются  весьма  актуальными.

Теория  вязких  течений  несжимаемой  жидкости  представляет  собой  один  из  важнейших  для  практики  и  наиболее  интересный  для  математических  исследований  раздел  гидродинамики.  Не  случайно  именно  в  задачах  динамики  вязких  течений  Лерэ  и  Шаудером  были  сделаны  первые  шаги  по  применению  методов  функционального  анализа,  а  в  последнее  время  уравнения  Навье-Стокса  стали  одним  из  первых  объектов  применения  численных  методов.  Многие  из  задач  динамики  вязкой  жидкости,  например  задача  о  численном  исследовании  течений  при  больших  до-  и  закритических  числах  Рейнольдса,  вплоть  до  настоящего  времени  не  решены  и  настоятельно  требуют  своего  решения. 

В  работе  известного  французского  математика  Роже  Темама  посвящении  достаточно  обстоятельному  изложению  вопросов  теории  и  в  особенности  вычислительным  аспектам  задач  динамики  вязкой  несжимаемой  жидкости,  рассмотрены  вопросы  существования,  единственности  и  регулярности  решений  краевых  задач  для  уравнений  Навье-Стокса  [8],  а  также  наиболее  общие  и  специальные  методы,  применимые  к  изучению  различных  видов  течения  жидкости  предложены  в  работах  Смагулова  Ш.С.,  Данаева  Н.Т.  [9]. 

Численными  методами  краевой  задачи  математической  физики  в  сложных  областях  рассматривались  во  многих  работах  зарубежных  и  отечественных  ученных  как  Вабищевича  П.Н.,  Отелбаев  М.О.,  Смагулов  Ш.С.,  Данаева  Н.Т.,  Балдыбек  Ж.,  Темирбеков  Н.М.  и  т.  д.

Уравнения  Навье-Стокса  является  уравнениями  типа  эвалюционного  характера.  Впервые  эта  идея  была  выдвинута  в  работе  [13]. 

Основные  элементы  технологии  построения  адаптивных  разностных  сеток  в  двумерных  и  трехмерных  областях,  основы  методов  построения  криволинейных  сеток  предоставлены  в  работах  [5;  6;  14;  15].

Численное  моделирование  установившихся  течений  жидкости  в  криволинейных  границах  производилось  в  большей  части  работ  на  основе  модели  вязкой  несжимаемой  жидкости.  Широкое  распространение  получили  алгоритмы,  основанные  на  уравнениях  Навье-Стокса,  использующие  метод  конечных  разностей. 

В  настоящее  время  существует  несколько  методов  для  численного  решения  краевых  задач  в  сложных  геометрических  областях,  как  метод  криволинейных  сеток  и  метод  фиктивных  областей.  Использование  метода  криволинейных  сеток  требует  преобразования  уравнения  в  криволинейные  координаты,  которое  имеет  более  сложный  вид,  чем  исходные  уравнения.  И  к  тому  же  многообразные  требования,  накладываемые  на  разностные  сетки,  делают  построения  криволинейных  сеток  сложной  математической  проблемой. 

Метод  фиктивных  областей  в  его  традиционной  постановке  прост  в  использовании  и  легко  реализуется  на  ЭВМ.  Но  его  недостатком  является  потеря  точности  из-за  присутствия  во  вспомогательных  уравнениях  малого  параметра,  который  приведет  к  плохой  обусловленности  системы  разностных  уравнений. 

В  данной  работе  рассматривается  численное  моделирование  течения  вязкой  несжимаемой  жидкости  в  дискретно  заданной  двусвязной  области  методом  дополненных  областей.  Предлагается  алгоритм  численной  реализации  предложенного  метода  в  работе  [1],  в  котором  отсутствует  малый  параметр.

Постановка  задачи 

Рассмотрим  уравнения  Навье-Стокса  в  двумерной  области    с  границей  . 

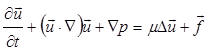                                   (1)

                                            (2)

с  начальными  и  граничными  условиями 

  при  , 

  при  ,  .         (3)

Здесь  х,у  —  декартовые  координаты,  t  —  время,    —  поле  скоростей,  p  —  отклонения  давления,    —  коэффициенты  вязкости. 

Вычислительный  алгоритм

Система  исходных  уравнений  (1)—(2)  записывалась  относительно  произвольной  криволинейной  системы  координат.  Согласование  полей  давления  и  скорости  осуществлялось  с  помощью  метод  фиктивных  областей,  модифицированного  для  расчета  задач.  Для  создания  дискретного  аналога  исходных  уравнений  вокруг  тел  сложной  геометрии  в  качестве  базовых  использовались  структурированные  сетки.  В  двусвязных  областях  применялись  многоблочные  вычислительные  технологии.  Такой  подход  позволило  выработать  единую  методологию  расчета  течений  вязкой  жидкости  в  двусвязных  областях. 

Система  исходных  уравнений  интегрировалась  численно  с  использованием  метода  дополненных  областей.  Производные  в  вязких  членах  аппроксимировались  центрально-разностной  схемой  второго  порядка.

Всю  рассматриваемую  область  непрерывного  изменения  аргумента  заменим  областью  дискретного  изменения,  то  есть  введем  сетку  следующего  вида: 

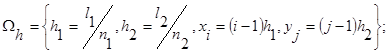
                                           (4)

В  работе  использовался  разнесенный  сеточный  шаблон,  в  котором  давление  и  дивергенция  определяются  в  узлах  разностной  сетки,  функция  тока  в  центре  разностной  ячейки,  а  компоненты  скорости  в  центрах  ее  граней. 

Использование  разнесенной  сетки  дает  возможность  связать  компоненты  скорости  в  соседних  точках  и  позволяет  избежать  появления  осцилляций  при  вычислении  поля  давления  (рисунок  1,  где    —  компонента  ,    —  компонента  ,    —  давление). 

Рисунок  1.  Шаблон  разнесенной  сетки

Компоненты  скорости,  давления,  и  функция  тока  определяются  в  точках:

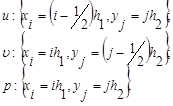
Разностные  аналоги  уравнений  (1),  (2) 

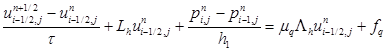         (1’)

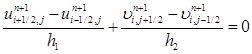                       (2’)

где 

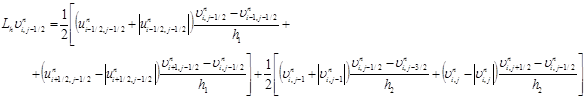
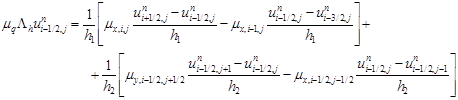
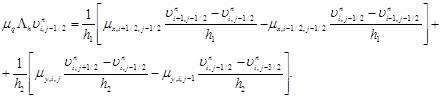
Получили  разностные  аналоги  соответствующих  конвективных  и  диффузионных  слагаемых.  Для  конвективных  слагаемых  использовалась  разностная  схема  с  учетом  знака,  и  в  неопределенных  узлах  сетки  значение  компонентов  определяется  осреднением.  Например 

.

Опишем  алгоритм  численного  решения  задачи  (1)—(3).  Для  численной  реализации  используем  метод  расщепления  по  физическим  процессам. 

В  первую  очередь  определим  промежуточные  значения  скорости    без  учета  давления:

;       (5)

Затем  по  промежуточному  значению  определяем  поле  давления.  Для  того  чтобы  получить  уравнение  для  давления  следующие  выражения

      (6)

     (7)

подставляем  в  (2’)  и  получим

       (8)

По  определенному  полю  давления  вычисляются  значения  компонент  скорости  с  помощью  (6)  и  (7).  Но  здесь  имеются  свои  проблемы,  отсутствие  граничных  условий  для  давления.  Во  избежание  этой  проблемы  во  втором  этапе  вместо  поля  давления  находим  значения  функции  тока  связанные  с  компонентами  скорости  следующими  выражениями  [6]:

,       (9)

.  (10)

Для  нахождения  значений  функции  тока  будем  иметь  выражения  следующего  вида 

;           (11)

где 

, 

.

Затем  находим  поле  скорости    с  помощью  выражении  (9),  (10).

Задачи  (5),  (6),  (7),  (8)  и  (5),  (9),  (10),  (11)  являются  эквивалентными. 

Для  использования  метода  дополненных  областей  при  численной  реализации  в  уравнения  (11)  добавляем  параметр,  описывающий  дополненную  область,  и  уравнения  (11)  приводится  в  следующий  вид:

  (12)

где  ,

  —  значение  функции  тока  на  границах  дополненной  области  и  фиктивной  области.  Предположим,  что  течения  движется  по  направлению    в  рисунке  2,  тогда  граничные  условия  определяется  следующим  образом:

,  ,  ,    при 

,  , 

при 

,  ,    при          (13)

,    при 

Пользуясь  физическим  смыслом  функции  тока  на  фиктивной  области  ,  значения  функция  тока  считали  константой: 

.  (14)

По  предложенному  методу  проведены  методические  расчеты.  Рассмотрим  криволинейную  двусвязную  область.  Рассматриваемую  область  дополним  до  прямоугольника  (рисунок  2),  чтобы  наложить  структурированные  прямоугольные  сетки.

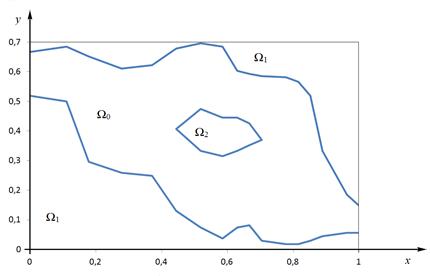
Рисунок  2.  Рассматриваемая  двусвязная  дискретно  заданная  область

Если  границы  физической  области  заданы  дискретным  множеством  точек  ,  тогда  определение  узлов  сетки  во  внешних  и  внутренних  границах  для  обеспечения  непрерывности  и  монотонности  границы  кривой  создает  некоторые  трудности,  а  также  при  численном  моделировании  часто  возникает  необходимость  изменении  количества  узлов  сетки. 

Для  обеспечения  непрерывности  и  монотонности  криволинейной  границы,  а  также  для  автоматизации  изменения  количества  узлов  сетки  использовался  кубическая  сплайн-интерполяция  следующего  вида  [9]:

                          (15)

Коэффициенты    определяются  следующим  образом:

                     (16)

                 (17)

здесь  . 

При  интерполировании  сплайном  возникают  проблемы  с  условиями  последовательности  аргументов  по  возрастанию,  так  как  рассматриваемая  нами  физическая  область  двусвязная.  Для  решения  проблем,  границы  двусвязной  области  нужно  разделить  на  соответствующие  интервалы.  Для  решения  уравнения  (17)  использовался  метод  скалярной  прогонки.

С  помощью  описанного  метода  получены  результаты  численных  расчетов  50×50  и  100×100  количествах  узлов  сетки.  На  рисунке  3  представлены  изолинии  функции  тока,  где  хорошо  видны  вихревые  движения  и  обтекание  препятствии.  А  на  рисунке  4  изображены  поля  вектора  скорости  и  границы  вихревых  движении.

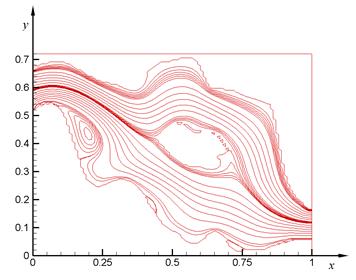
Рисунок  3.  Изолинии  функции  тока

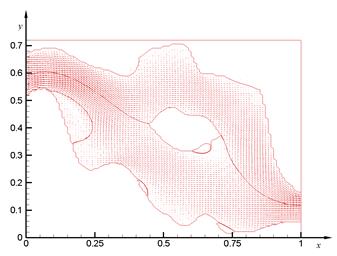
Рисунок  4.  Поле  вектора  скорости  и  границы  вихревых  движении

Заключение

Современные  требования  к  достоверности  получаемых  численных  результатов  и  надежности  программно-методического  обеспечения  требуют  тщательно  тестирования  и  верификации  разработанного  комплекса  программ.  Тестирование  разработанной  методики,  алгоритмов  и  комплекса  программ  выполнено  на  задачах  о  развитии  течения  вязкой  несжимаемой  жидкостью  [3]. 

Данная  методика  моделирования  течения  несжимаемой  жидкости  в  сложных  двумерных  геометрических  областях,  избавит  нас  от  малого  параметра  и  вычисления  давления,  для  которого  в  постановке  задачи  отсутствуют  граничные  условия.

Рассматривалась  два  метода  решения  задачи.  Первый  метод  основан  на  построении  разностной  задачи  в  переменных  функция  тока  и  вихрь  скорости  с  использованием  условия  однозначности  давления.  Численное  решение  эллиптического  уравнения  для  функций  тока  находится  как  сумма  решений  двух  простых  задач  эллиптического  типа.  Одна  задача  является  с  однородными  граничными  условиями,  а  другая  с  однородным  уравнением.  Вторым  методом  к  решению  поставленной  задачи  является  метод  фиктивных  областей  с  продолжением  по  младшим  коэффициентом.  Этот  метод  не  требует  удовлетворения  условия  однозначности  давления  и  является  простым  в  реализаций.

Список  литературы:

1.Балдыбек  Ж.  Метод  дополненных  областей  для  нелинейной  краевой  задачи  океана  //  Математическиий  журнал,  Алматы,  —  2002.  —  Т.  2.  —  №  2.  —  С.  41—50.

2.Вабищевич  П.Н.  Методы  фиктивных  областей  в  краевых  задачах  математической  физики.  М.:  МГУ,  1991.  —  278  с.

3.Вольцингер  Н.Е.,  Клеванный  К.А.,  Пелиновский  Е.Н.  Длинноволновая  динамика  прибережный  зоны.  Ленинград:  Гидрометеоиздат,  1989.  —  272  с.

4.Данаев  Н.Т.  Об  одной  возможности  численного  построения  ортогональных  сеток  //  Числен.  методы  механ.  сплошной  среды.  Новосибирск,  1983.  —  Т.  14.  —  №  3.  —  с.  42—53.

5.Лисейкин  В.Д.  Обзор  методов  построения  структурных  адаптивных  сетокю  /  Журнал  Вычислительных  математики  и  математической  физики.  Том  36.  —  1996.  —  №  1.  —  39  с.

6.Лисейкин  В.Д.,  Шокин  Ю.И.,  Васева  И.А.,  Лиханова  Ю.В.  Технология  построения  разностных  сеток.  Новосибирск:  Наука,  2009.  —  414  с.

7.Мухаметжанов  А.Т.,  Отельбаев  М.О.,  Смагулов  Ш.С.  Об  одном  методе  фиктивных  областей  для  нелинейных  краевых  задач  //  Вычисл.  технологии.  —  1998.  —  Т.  3.  —  №  4.  —  С.  41—64.

8.Самарский  А.А.  Теория  разностных  схем.  М.:  Наука,  1983.  —  616  с. 

9.Смагулов  Ш.С.,  Данаев  Н.Т.,  Темирбеков  Н.М.  Численное  решение  уравнений  Навье-Стокса  для  несжимаемой  жидкости  в  каналах  с  пористой  ставкой  //  Прикладная  механика  и  техническая  физика.  Новосибирск,  —  1995.  —  Т.  36.  —  №  5.  —  с.  21—29.

10.Смагулов  Ш.С.,  Отельбаев  М.О.  О  новом  методе  приближенных  решений  нелинейных  уравнений  в  произвольной  области  //  Вычисл.  технологии.  —  2001.  —  Т.  6.  —  №  6.  —  С.  93—107.

11.Смагулов  Ш.С.  Метод  фиктивных  областей  для  уравнений  Навье-Стокса  //  Препр.  АН  СССР  Сиб.  отделение  ВЦ,  Новосибирск,  1979.

12.Сироченко  В.П.  Численное  моделирование  конвективных  течений  вязкой  жидкости  в  многосвязных  областях  //  Труды  Международной  конференции  RDAMM-2001,  Вычисл.  технологии.  —  Новосибирск.  —  2001.  —  Т.  6.  —  Ч.  2.  —  Спец.  выпуск  —  С.  554—562.

13.Темирбеков  Н.М.,  Мнафиянов  Е.М.,  Малгаждаров  Е.А.  Баилова  А.  Тепло-массобмен  несжимаемой  жидкости  в  двусвязных  областях  с  произвольной  криволинейной  границей  //  Математическое  моделирование  научно-технологических  и  нефтегазодобывающей  промышленности:  Материалы  VI  Казахстанско-Российской  международной  научно-практической  конференции  11—12  октября  2007  г,  г.  Астана  /  ЕНУ  им.  Л.  Гумилёва.  Астана,  2007.  —  С.  317—322.

14.Хакимзянов  Г.С.,  Лисейкин  В.Д.,  Лебедев  А.С.  Разработка  методов  построения  адаптивных  сеток  /  Вычислительные  технологии.  —  2002.  —  Т.  7.  —  №  3.

15.Шокин  Ю.И.,  Данаев  Н.Т.,  Хакимзянов  Г.С.,  Шокина  Н.Ю.  Лекции  по  разностным  схемам  на  подвижных  сетках.  В  3  ч.:  Часть  2.  Задачи  для  уравнений  в  частных  производных  с  двумя  пространственными  переменными  :  учеб.  пособие.  Алматы:  Казахсий  нац.  Ун-т  им.  Аль-Фараби,  2008.  —  184  с.

16.Шокин  Ю.И.,  Данаев  Н.Т.,  Хакимзянов  Г.С.,  Шокина  Н.Ю.  Лекции  по  разностным  схемам  на  подвижных  сетках.  В  3ч.:  Часть  2.  Задачи  для  уравнений  в  частных  производных  с  двумя  пространственными  переменными  :  учеб.  пособие.  Алматы:  Казахсий  нац.  Ун-т  им.  Аль-Фараби,  2008.  —  184  с.

17.Яненко  Н.Н.,  Данаев  Н.Т.,  Лисейкин  В.Д.  О  вариационном  методе  построения  сеток  //  Численные  методы  механики  сплошной  среды.  —  Новосибирск.  —  1977.  —  Т.  8.  —  №  4.  —  с.  157—163. 

18.Thompson  J.F.,  Warsi  Z.U.A.,  Mastin  C.W.  Numerical  grid  generation,  foundations  and  applications.  1985,  New  York,  etc.:  Elsevier.