МЕТОДЫ  СПЕКТРАЛЬНОГО  АНАЛИЗА  В  ОЦЕНКЕ  РЕЗУЛЬТАТОВ  МОНИТОРИНГА  РИТМА  СЕРДЦА  ПРИ  ЭМОЦИОНАЛЬНОЙ  И  УМСТВЕННОЙ  НАГРУЗКЕ

Осипенко  Александр  Викторович

соискатель,  НИУ  «МЭИ»,  РФ,  г.  Москва

Е-mail :  avo77@yandex.ru

METHODS  OF  SPECTRAL  ANALYSIS  IN  RECOGNITION  OF  THE  HRV-MONITORING  RESULTS  DURING  EMOTIONAL  AND  MENTAL  STRESS

Alexander  Osipenko

applicant,  National  Research  University  "MPEI",  Russia,  Moscow

Аннотация

В  статье  анализируется  применение  методов  спектрального  анализа  для  обработки  данных  мониторинга  ритма  сердца,  и  предлагается  методика  предварительной  обработки  измерений  для  исключения  физиологического  шума,  трендов  и  погрешностей  сигнала  в  процессе  длительной  регистрации  ВСР  при  эмоциональной  и  умственной  нагрузке.

ABSTRACT

The  article  analyzes  the  application  of  methods  of  spectral  analysis  for  data  of  HRV-monitoring,  and  proposes  a  methodology  for  pre-processing  of  the  measurements  to  exclude  physiological  noise,  trends  and  errors  of  the  signal  in  the  longtime-registration  of  HRV  during  emotional  and  mental  stress

Ключевые  слова:  ВСР;  методы  и  алгоритмы  спектрального  анализа;  преобразования  Фурье;  корреляционная  функция;  спектральная  плотность.

Keywords:  HRV;  methods  and  algorithms  of  spectral  analysis;  Fourier  transform;  correlation  function;  spectral  density.

В  последние  годы  показатели  вариабельности  сердечного  ритма  (ВСР)  находят  все  более  широкое  применение,  как  в  клинической  практике,  так  и  в  оценке  функциональных  состояний  в  физиологии  труда,  в  том  числе  и  для  оценки  эмоциональной  и  умственной  нагрузки.  При  этом  для  получения  сопоставимых  результатов  необходимо  обеспечить  условие  стационарности,  что  практически  невозможно  при  длительной  регистрации  особенно  в  условиях  трудовой  деятельности.  Это  обуславливает  необходимость  применения  математических  методов  обработки  данных,  для  исключения  физиологического  шума  и  погрешностей  сигнала,  исследованию  этих  методов  и  разработке  методики  оценки  ВСР  при  длительной  регистрации  посвящена  данная  работа.

Как  известно  ВСР  наблюдается  даже  в  состоянии  покоя,  а  непостоянство  интервала  между  кардиоциклами  находится  в  пределах  некой  средней  величины,  являющейся  оптимальной  для  рассматриваемого  функционального  состояния  организма.  Причем  при  любом  изменении  (положения  тела,  позы  и  пр.)  частота  сердечных  сокращений  начинает  подстраиваться  под  новый  функциональный  уровень,  образуя  тренды,  сохраняющиеся  и  некоторое  время  после  окончания  двигательной  активности,  аналогичное  влияние  оказывает  и  суточная  ритмика,  выражающаяся  проявлением  периодической  составляющей  физиологических  функций.

Вместе  с  тем,  стандартами  [2]  предусмотрены: 

·     5  минутные  регистрации  RR  интервалов,  для  которых  нет  сложностей  обеспечения  покоя  и  стационарности,

·     и  24  часовые,  где  включаются  циркадные  колебания,  и  позные  тренды,  поскольку  обеспечить  стационарность  при  длительной  регистрации  сложно. 

Исключение  названных  факторов  обычно  обеспечивается  применением  спектрального  анализа  RR-интервалов  и  прежде  всего  преобразованиями  Фурье,  которые  программно  предусмотрены,  как  в  обычных  холтеровских  мониторах,  так  и  в  специализированных  стресс  системах.  Но  различия  в  программной  реализации  данного  метода  в  приборах  разных  производителей,  могут  вносить  существенные  расхождения  в  получаемые  результаты. 

В  большинстве  систем  мониторинга  ритма  сердца  результаты  измерения  RR  интервалов,  оцениваются  как  временные  ряды,  и  к  ним  для  исключения  периодических  колебаний,  применяются  методы  спектрального  анализа  (преобразования  Фурье).  Между  тем  RR-интервал  —  это  интервал  времени  от  зубца  R  до  зубца  R  или  расстояние  между  ними  на  ЭКГ  (по  оси  х).  Ввиду  этого,  ряд  интервалов  RR  на  интервалограмме  не  вполне  может  рассматриваться  как  временной  ряд,  так  как  аргументом  является  не  время,  а  порядковые  номера  кардиоцикла,  длительность  которых  непостоянна,  что  приводит  к  неравномерности  шага  временного  ряда.  Поэтому  предлагаются,  геометрические  методы  или  интерполяция,  и  хоть  это  не  совсем  корректно,  но  методы  анализа  временных  рядов  применяются  к  RR-интервалам  достаточно  широко.

Как  и  большинство  других  видов  анализа,  анализ  временных  рядов  предполагает,  что  данные  содержат  систематическую  составляющую  и  случайный  шум,  который  затрудняет  обнаружение  регулярных  компонент.  Большинство  методов  исследования  временных  рядов  включает  различные  способы  фильтрации  шума,  позволяющие  увидеть  регулярную  составляющую  более  отчетливо  [1]. 

Разрабатываемая  методика  предполагает  следующие  способы  фильтрации  шума:  1)  исключение  погрешностей  и  ошибок  измерений  (в  случае  воздействия  помех  или  пропуска  сигналов  из-за  ненадежной  фиксации  датчика)  и  2)  исключение  случайного  шума  и  трендов,  образуемых  циркадной  ритмикой,  сменой  позы  и  другой  физической  активностью.

Для  исключения  ошибок  измерений,  получаемых  в  процессе  мониторинга  ритма  сердца,  предусмотрена  предварительная  оценка  результатов,  и  их  корректировка.  Из  рядов  данных  исключаются  измерения,  находящиеся  вне  заданного  интервала,  границы  которого  назначаются  как  предельно  возможные  в  условиях  исследования  значения  измеряемых  параметров.  Также  предварительная  обработка  предусматривает  применение  динамического  спектра  с  возможность  установки  времени  начала  и  конца  стационарных  участков  и  исключения  из  анализа  части  данных  начального  и  конечного  этапов  измерений,  и  нестационарных  участков,  где  имелась  физическая  двигательная  активность,  с  возможностью  замены  некоторых  измерений,  средним  значением  ряда.

В  целях  исключения  периодической  составляющей  циркадной  ритмики,  и  случайного  шума  и  трендов,  образуемых  сменой  позы,  не  выделенных  предварительной  оценкой  измерений:

·     обеспечиваем  получение  временного  ряда  с  равномерным  шагом  применением  преобразования  Фурье  не  к  интервалограмме,  а  к  функции  n(t)  (изменяя  данные  ряда  с  RR-интервалов  на  соответствующие  значения  пульса);

·       применяем  методы  вычисления  корреляционных  функций  и  спектральных  плотностей.  Данную  процедуру  подробно  рассмотрим  ниже.

Главной  задачей  вычисления  корреляционных  функций  и  спектральных  плотностей  является  исключение  тренда  и  сглаживание  высокочастотных  компонентов.  Для  этого  экспериментально  полученная  последовательность  RR  интервалов  —  (i),  которую  можно  представить  в  виде  суммы  медленно  меняющейся  нестационарной  составляющей    (i),  и  случайной  составляющей  (i),  где  i  =  1,  N;  (N  —  число  RR  интервалов  последовательности)  подвергается  спектральному  анализу.  Нестационарная  составляющая  практически  тождественна  рассмотренным  выше  медленным  изменениям  частоты  пульса.  Для  получения  информативного  спектра  случайной  составляющей  (i)  можно  воспользоваться  вычислениями  нормированной  корреляционной  функцию  R(К)  относительно  скользящего  среднего,  которая  тождественна  (i).

В  данном  случае,  скользящая  средняя  несет  в  себе  ряд  спектральных  составляющих,  исключая  их  из  общего  спектра  (i).  Эти  искажения  можно  легко  учесть,  поскольку  скользящее  среднее  последовательных  отсчетов  значений  к  некоторой  гармоники  с  периодом  Т  (выраженным  числом  RR  интервалов,  и  весовыми  коэффициентами    (где    —  интервал  усреднения))  дает  в  (i)  гармонику  с  тем  же  периодом  Т,  но  с  амплитудой  в  l  раз  меньше  амплитуды  первоначального  ряда.

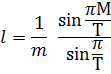
Спектр  остатка  (i)  при  этом  полностью  сохраняет  все  гармоники  с  периодом  Т,  а  амплитуда  гармоник  с    уменьшается  не  более,  чем  в  два  раза.  Это  обуславливает  выбор  интервала  усреднения  по  длительности  наибольшего  периода  Т_макс  в  процессе  (i),  который  интересен  для  исследования,  из  условия:

  —  минимальная  частота  в  спектре  (i).

Скользящее  среднее  вычисляем  по  формуле:

(i)  = 

где  ,  а  P+1(i)  не  может  вычисляться  для  первых  и  последних  членов  ряда  (i).

Определяем  нормированную  корреляционную  функция  R(К):

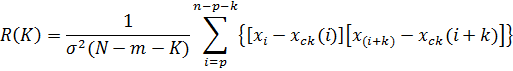
где    —  дисперсия  процесса  (i)  относительно  скользящего  среднего,  а  К  –  порядковый  номер  значения  R(К).  Число  N_К  (общее  число  значений  нормированной  корреляционной  функции)  обычно  выбирают  не  менее  (N-2p)/z  при  z  =  2+5,  но  не  более  80—120,  т.  к.  дальнейшее  увеличение  числа  N_K  мало  влияет  на  точность  измерений  спектра. 

Вычисляем  спектр  S(n)  в  дискретные  моменты:

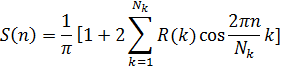
где  n  —  дискретная  частота  0,1,2…,  связанная  частотой    и  круговой  частотой  . 

При  данном  способе  выделения  тренда,  полученные  спектры  характеризуются  большим  число  пиков,  и  появлением,  так  называемых  боковых  пиков,  обусловленных  незатухающим  характером  коррелограммы.  Ввиду  чего  целесообразно  сглаживание  таких  спектров,  способом  скользящей  средней  (или  медианное  сглаживание)  с  интервалом  усреднения  m_S  =  3÷5  или  P_S  =  1÷2.

В  результате  соответствующих  преобразований  выражение  для  вычисления  спектра  имеет  вид:

Ṧ(n)=  для 

Полученный  спектр  достаточно  полно  отражает  частоты,  для  которых  в  коррелограмме  укладываются  не  меньше  двух  периодов,  т.  е.  частоты  с  периодом  Т_макс

Требования  к  интервалу  сглаживания  и  длительности  коррелограммы  находим  из  соотношений:

;  ,

Поскольку  S(n)  является  периодической  функцией  с  периодом  2.  Т.к.  ,  спектр  симметричен  относительно  Поэтому  его  достаточно  найти  только  для  таких  n,  при  которых  аргумент  косинуса  в  формуле  меняется  от  0  до  ,  т.  е.  0.  Число  N_S=N_k/2  определяет  наибольшее  число  точек,  для  которых  необходимо  вычислять  спектр.  Для  оценки  реальной  интенсивности  каждой  гармоники  полученного  дискретного  спектра  достаточно  ординаты  умножить  на  ,  а  в  аргументе  дискретную  частоту  n  заменить  на    —  среднее  арифметическое  ряда  (1  i).  Тогда  аргумент  выражен  в  Гц,  а  ордината  в  .

Для  наглядного  представления  веса  каждой  гармоники  целесообразно  вычислить  нормированный  спектр:

В  этом  случае  каждая  ордината  спектра  характеризует  долю  общей  интенсивности  спектра  (в  %),  приходящуюся  на  данную  гармонику.

Таким  образом,  предложенные  подходы  и  методы  спектрального  анализа  позволяют  корректно  выделять  периодические  циркадные  компоненты  и  тренды,  обусловленные  изменениями  положения  тела,  позы,  двигательной  активности.  Что  обеспечивается  получением  временного  ряда  с  равномерным  шагом,  или  получением  размерности  анализируемых  периодов  в  герцах  и  в  процентах  спектральной  плотности.

Применение  методики  на  практике  позволяет  более  точно  учитывать  динамику  изменения  отдельных  составляющих  спектра  RR-интервалов,  и  соответственно  учитывать  их  влияние  при  оценке  функциональных  состояний,  в  том  числе  и  индивидуальных  реакций  на  эмоциональную  и  умственную  нагрузку.

Список  литературы:

1.Андерсон  Т.  Статистический  анализ  временных  рядов  М.  Мир  1976,  —  756  с.

2.Task  force  report  of  European  Society  of  Cardiology  and  the  North  American  Society  of  Pacing  and  Electrophysiology.  Heart  rate  variability:  standards  of  measurement,  physiological  interpretation  and  clinical  use.  Circulation  1996:  —  р.  1043—1065.