НЕКОТОРЫЕ  СВОЙСТВА  ФУНКЦИЙ,  ЗАДАНЫХ  НЕЯВНО

Гладышева  Кристина  Александровна

студент  Московского  государственного  университета  информационных  технологий,  радиотехники  и  электроники,  РФ,  г.  Серпухов

E-mail:  kristusha -malusha@mail.ru

Таперечкина  Вера  Алексеевна

канд.  физ.-мат.  наук,.  Доцент  Московского  государственного  университета  информационных  технологий,  радиотехники  и  электроники,  РФ,  г.  Серпухов

 

SOME  PROPERTIES  OF  IMPLICIT  FUNCTION

Christina  Gladysheva

Student  Moscow  State  University  of  Information  Technologies,  Radio  Engineering  and  Electronics,  Russia,  Serpukhov

Vera  Taperechkina

candidate  of  Physical  and  Mathematical  Sciences,  docent  Moscow  State  University  of  Information  Technologies,  Radio  Engineering  and  Electronics,  Russia,  Serpukhov

 

АННОТАЦИЯ

В  работе  рассмотрены  некоторые  способы  нахождения  производных  и  дифференциалов  первого  и  второго  порядков  для  неявных  функций  одного  и  двух  переменных,  в  том  числе  неявных  функций,  заданных  системой.

ABSTRACT

In  this  work  we  reviewed  some  methods  of  finding  of  first  and  second  differentials  for  Implicit  function  with  one  and  two  Variables  including  Implicit  functions  defined  by  system.

 

Ключевые  слова :  неявная  функция;  частные  производные;  дифференциал.

Keywords :  Implicit  function,  Partial  derivatives,  differential.

 

1.  Теоретические  предпосылки.

Будем  предполагать,  что  выполняемы  требования  теоремы  существования  неявной  функции  [1]  (и  ее  обобщения  для  случая  нескольких  переменных  [1]).

Теорема. 

Пусть  функция  F(x,  y)  непрерывна  в  некоторой  окрестности  точки  (,)  и  имеет  в  этой  окрестности  непрерывные  частные  производные  ,  .  Если  F(,)=0,  (,)0,  то  существует  единственное  решение    уравнения  F(x,  y)=0.  Функция    удовлетворяет  условию  и  имеет  непрерывную  производную

 

(=  -    (1)

 

Будем  предполагать  также  выполнение  условий  теоремы  Шварца  о  равенстве  смешанных  производных  [1].

2.  Формула  для  второй  производной  неявной  функции  одной  переменной.

Формулу  (1)  можно  получить  из  равенства  F(x,  y)=0,  если  взять  от  него  производную  по  x  с  учетом  того,  что  y=y(x),  то  есть  ,  а  именно,

 

=0  (2)

 

Если  в  тождестве  еще  раз  взять  производную  по  x,  с  учетом  того,  что    зависят  и  от  x  и,  то  получим  новое  тождество:

 

+    +  (+)=0  или

+2    ++=0

 

Отсюда,  используя  (1)  получаем  формулу:

 

  (3)

 

Так  как  и  ,  то  формулы  (1)  и  (3)  позволяют  найти  дифференциалы  первого  и  второго  порядка,  соответственно.

Обычно  метод  нахождения  второй  производной  для  функции,  заданной  неявно,  сводится  к  повторному  дифференцированию  данного  в  задаче  условия,  что  фактически  приводит  к  необходимости  вывода  на  каждом  конкретном  примере  формулы  (3).  Использование  готовой  формулы  (3)  существенно  упрощает  решение.

Пример  1.  Найти  производную  второго  порядка  функции,  заданной  неявно  уравнением:

 

 

Решение.  Обозначим  .

Найдем  от    все  частные  производные  первого  и  второго  порядка:

 

.

 

Отсюда  по  формуле  (3)  получаем  после  преобразования  ответ:

Ответ 

Пример  2.  Найти    в  точке  М(0;  1),  если  функция  задана  неявно  уравнением:

 

 

Решение.  Обозначим  .  Последовательно  находим  производные  от  .

 

 

По  формуле  (1)  получаем    и,  следовательно,  .  По  формуле  (3)  получаем    и,  следовательно,  .

Ответ. 

3.  Вывод  формул  для  вторых  частных  производных  функции  двух  переменных,  заданной  неявно.

Рассмотрим  функцию  двух  независимых  переменных  x  и  y,  заданную  неявно  уравнением  F(x;  y;  z)=0.  Фиксируя  по  очереди  переменные  у  и  х,  получим  из  формулы  (1)  соответственно:

 

  и    (4)

 

Найдем  формулы,  выражающие  через  частные  производные  от  F(x;  y;  z).  Для  этого  от  (4)  повторно  берем  производную.  При  повторном  взятии  производной  от  первой  из  формул  (4)  по  переменной  х  следует  учесть,  что  у  фиксирована,  а  z,  которое  содержится  в    и  ,  зависит  от  x.  Таким  образом,    и    зависят  от  x  непосредственно,  а  также  через  z.

 

 

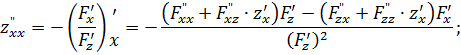
С  учетом  (4)  получим 

 

 

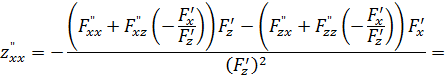
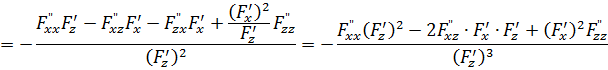
Таким  образом,  получена  формула:

 

  (5)

 

Аналогично

 

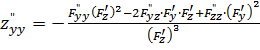  (6)

 

Формулы  (5)  и  (6),  конечно,  согласуются  с  (3).  Найдем  теперь  смешанную  производную  второго  порядка.  Для  этого  от  первой  из  формул  (4)  берем  производную  по  у.  Отметим,  что  у  входит    и    как  непосредственно,  так  и  через  z.

 

 

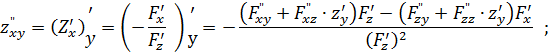
С  учетом  (4)  получим:

 

 

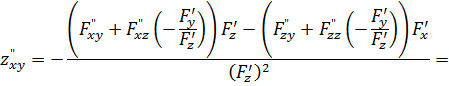
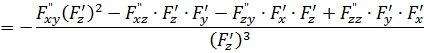
Таким  образом,  получена  формула:

 

  (7)

 

Для  нахождения  первого  и  второго  дифференциала  подставляем  (4),  (5),  (6),  (7)  в  известные  формулы  [1].

 

  (8)

  (9)

 

Пример3.  Найти  первый  и  второй  дифференциал  от  функции  функцию,  заданной  неявно  уравнением:

Найти 

Решение:  Обозначим  F(x;  y;  z)=,  М(1;  -1;  0).  Находим  последовательно  все  частные  производные  первого  и  второго  порядка  в  точке  М(1;  -1;  0).

По  формулам  (4),  (8)  получаем:

 

 

Далее  по  формулам  (5),  (6),  (7),  (9)  получаем:

 

  ;

 

 

 

.

 

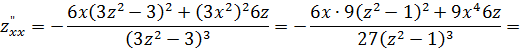
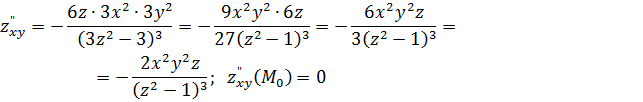
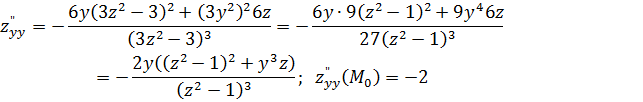
Пример  4  [2].

Найти  ,  если  z=1  в  точке    и  функция  ,  задана  неявно  уравнением:

 

 

Решение.  Обозначим  F(x;  y;  z)=;  М(1;  0;  1).  Находим  последовательно  все  частные  производные  первого  и  второго  порядка  в  точке  М(1;  0;  1).

По  формулам  (5),  (6),  (7),  (9)  получаем:

 

; 

=.

 

4.  Производные  неявных  функций  одной  переменной,  заданных  системой.

Пусть  функции  F(х;  y;  z)  и  G(х;  y;  z)  непрерывны  и  имеют  непрерывные  частные  производные  в  точки  (  и  некоторой  ее  окрестности.  Точка  (  удовлетворяет  системе:

 

  (10)

 

Пусть  определитель 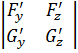 отличен  от  0  в  точке  (.  Тогда  в  некоторой  окрестности  точки  (  система  (10)  определяет  две  функции  y=y(x)  и  z=z(x),  такие  что  y(;  z(.  Функции  y(х)  и  z(х)  непрерывны  и  имеют  производные  [1].

Способ  нахождения  этих  производных  состоит  в  том,  что  от  уравнений  системы  (10)  берется  производная  по  х  и  далее  из  полученной  системы  находится  ,  а  именно:

 

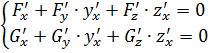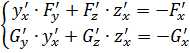  или    (11)

 

Система  (11)  линейная  по  ,  и  ее  определитель  отличен  от  0.  По  правилу  Крамера  из  (12)  получим: 

 

;  =;  (12)

 

Для  вычисления  вторых  производных  следует  от  уравнений  системы  (11)  еще  раз  взять  производную  по  х  и  далее,  используя  уже  известные  ,  найти  .

Пример5.  Функции  y(x),  z(x)  заданы  неявно  системой 

 

 

 

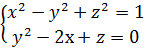
Найти  ,  если  у(1)=1;  z(1)=1.

Решение.  Возьмем  производную  по  х  от  уравнений  системы,  учитывая,  что  х  —  независимая  переменная,  y=y(х),  z=z(х). 

 

  (13)

 

Отсюда:

 

 

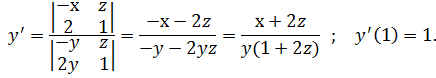
Возьмем  еще  раз  производную  по  х  от  уравнений  системы  (13),  тогда  получим

 

 

Умножим  первое  уравнение  на  2  и  далее  сложим  уравнения,  тогда

 

  .

 

Из  второго  уравнения  последней  системы  найдем

 

  .

.

 

5.  Производные  неявных  функций  двух  переменных,  заданных  системой.

Пусть  теперь  система  двух  уравнений  задает  две  функции,  где  —  независимые  переменные

 

 

способы  нахождения  частных  производных  и  дифференциалов  первого  и  второго  порядков.

Пример  6  [3].

Найти  du,  dv,  ,  если  u(х,  у)  и  v(х,  у)  заданы  системой 

 

 

  Преобразуем  условия 

 

  (14)

 

Берем  от  системы  (14)  производную  по  x,  при  этом  y  считаем  постоянным,  .

 

 

 

Решая  эту  систему,  например,  по  правилу  Крамера,  получим:

 

 

Берем  от  системы  (14)  производную  по  у,  при  этом  х  считаем  постоянным,  .

 

 

Решая  эту  систему,  например,  по  правилу  Крамера,  получим: 

 

 

Так  как  то  получим  ответы  для  первых  дифференциалов.

 

 

  (15)

 

Первый  дифференциал  можно  найти,  если  к  системе(14)  применить  операцию  взятия  дифференциала  с  учетом  инвариантности  формы  1-ого  дифференциала  и  свойств  дифференциала  ;

;

).

 

 

 

  (16)

 

Из  первого  уравнения  .  Подставим  во  второе  уравнение.

 

 

Найдем  отсюда  du:

 

 

Аналогично,  если  из  первого  уравнения  системы  (16)  выразить  du  и  подставить  во  второе  уравнение  системы  (16),  получим:

 

 

И  вновь  получили  ответ  (15).

Второй  дифференциал  аналогично  можно  найти  двумя  способами.  Во  втором  способе  (метод  взятия  дифференциала)  при  повторном  взятии  дифференциала  следует  обратить  внимание  на  то,  что    Рассмотрим  этот  способ.  Берем  дифференциал  от  (16).  Первое  уравнение  системы  (16)  дает: 

 

 

Подставляем  в  это  уравнение    и  решаем  его  относительно  .
 

 

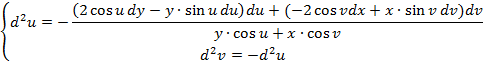
Здесь  du  и  dv  найденные  нами  ранее  значения  (15).

 

Список  литературы:

1.Архипов  Г.И.,  Садовничий  В.А.,  Чубариков  В.Н.  Лекции  по  математическому  анализу,  М.:Дрофа,  2004.

2.Виноградова  И.Л.,  Олехник  С.Н.,  Садовничий  В.А.  Задачи  и  упражнения  по  математическому  анализу  М.В.Ш.,  2002.

3.Демидович  Б.П.  Сборник  задач  и  упражнений  по  математическому  анализу,  М.:Наука,  1990.