ДИФФУЗИОННЫЙ  ТРАНСПОРТ  В  ЦИЛИНДРЕ  ПЕРЕМЕННОГО  СЕЧЕНИЯ

Зицерман  Владимир  Юрьевич

канд.  физ.-мат.  наук,  ведущий  научный  сотрудник  Объединенного

института  высоких  температур  Российской  Академии  наук,  РФ,  г.  Москва

E -mail:  vz1941@mail.ru

Махновский  Юрий  Абрамович

канд.  физ.-мат.  наук,  ведущий  научный  сотрудник  Института

нефтехимического  синтеза  им.  А.В.  Топчиева  Российской  Академии  наук,  РФ,  г.  Москва

E -mail:  yuam@jps.ac.ru

Антипов  Анатолий  Евгеньевич

научный  сотрудник  факультета  фундаментальной  физико-химической  инженерии  Московского  государственного  университета,  РФ,  г.  Москва

E-mail: 

DIFFUSIONAL  TRANSPORT  IN  A  TUBE  WITH  VARIABLE  CROSS-SECTION

Zitserman  Vladimir

leading  scientist,  Candidate  of  Science,  Joint  Institute  for  High  Temperatures,  Russian  Academy  of  Sciences,  Russia,  Moscow

Makhnovskii  Yurii

leading  scientist,  Candidate  of  Science,  Topchiev  Institute  of  Petrochemical  Synthesis,  Russian  Academy  of  Sciences,  Russia,  Moscow

Antipov  Anatoly

postgraduate  student,  Moscow  State  University,  Faculty  of  Fundamental  Physics  and  Chemical  Engineering,  Russia,  Moscow

Работа  выполнена  при  поддержке  РФФИ  —  проект  №  14-03-00343.  В.Ю.З.  благодарит  за  поддержку  в  рамках  программы  ПРАН  №  43  «Фундаментальные  проблемы  математического  моделирования»  (координатор  —  акад.  Бетелин  В.Б.).

АННОТАЦИЯ

Рассмотрена  задача  о  дрейфе  и  диффузии  частицы  в  трубке,  состоящей  из  периодически  распределенных  сегментов  малого  и  большого  радиусов,  под  действием  силы,  направленной  вдоль  оси  трубки.  Предложен  приближенный  подход,  позволяющий  аналитически  рассчитать  эффективные  транспортные  коэффициенты  в  условиях  сильного  сноса.  Полученные  формулы  для  эффективной  подвижности  и  эффективного  коэффициента  диффузии  хорошо  согласуются  с  данными  компьютерного  моделирования,  выполненного  методом  броуновской  динамики.

ABSTRACT

We  consider  the  problem  of  drift  and  diffusion  of  a  particle  in  a  tube,  consisting  of  periodically  distributed  segments  of  small  and  large  radius,  under  the  action  of  force  directed  along  the  tube  axis.  An  approximate  approach  is  proposed  which  provides  analytical  treatment  of  effective  transport  coefficients  under  strong  bias  conditions.  Equations  derived  for  the  effective  mobility  and  effective  diffusivity  are  in  good  agreement  with  computer  simulation  data  obtained  by  the  Brownian  dynamics  method.

Ключевые  слова:   диффузия;  дрейф;  подвижность;  броуновская  динамика.

Keywords:   diffusion;  drift;  mobility;  brownian  dynamics.

В  связи  с  исследованиями  транспорта  в  микронеоднородных  природных  и  биологических  объектах,  в  последние  годы  возник  повышенный  интерес  к  задаче  о  дрейфе  и  диффузии  в  квазиодномерных  периодических  структурах  переменного  сечения  под  действием  внешней  силы.  Традиционно  используется  приближение  Фика-Джекобса  [3],  которое  позволяет  при  слабой  вариации  сечения  свести  задачу  к  одномерной  (1D)  за  счет  введения  энтропийного  потенциала.  Этот  подход  не  применим,  когда  имеют  место  резкие  скачки  сечения.  Вместе  с  тем,  одномерное  описание  в  терминах  эффективных  диффузии  и  сноса  остается  оправданным  на  масштабах,  превосходящих  период  структуры.  В  данной  работе  показано  как  найти  эффективные  транспортные  коэффициенты,  подвижность    и  коэффициент  диффузии  ,  частицы,  движущейся  под  действием  силы    в  структуре,  показанной  на  рис.  1.

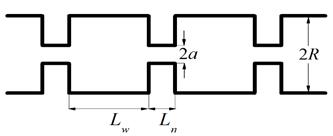
Рисунок  1.  Схема  модели:  частица  движется  в  трубке,  состоящей  из  чередующихся  широких  и  узких  участков,  радиусы  и  длины  которых  равны    и  ,  и    и  ,  соответственно

Предлагаемый  подход  основан  на  том  факте,  что  частица,  движущаяся  в  этих  условиях,  может  находиться  только  в  двух  состояниях:  (1)  подвижном,  когда  она,  пребывая  цилиндре  радиуса  ,  движется  свободно  со  скоростью    (  подвижность  в  свободном  пространстве)  и  (2)  неподвижном,  когда  она,  попадая  в  широкий  участок,  оказывается  за  пределами  этого  цилиндра  и,  будучи  прижатой  к  стенке,  не  участвует  в  продольном  движении.  Таким  образом,  вычисление    сводится  к  нахождению  вероятности    обнаружить  частицу  подвижном  состоянии. 

Для  решения  этой  задачи  введем  вероятности    обнаружения  частицы:  в  цилиндре  радиуса    в  широком  участке;  вне  этого  цилиндра  в  широком  участке;  в  узком  цилиндре.  Наряду  с  условием  нормировки,  эти  вероятности  удовлетворяют  еще  двум  соотношениям.  Одно  из  них  связывает    и  ,  отражая  тот  факт,  что  они  пропорциональны  длинам  соответствующих  участков.  Соотношение  между    и    определяется  распределением  частиц  в  сечении  радиуса    широкого  участка.  Ранее  было  показано  [2;  4],  что  в  отсутствие  узкого  участка,  ,  когда  в  трубке  периодически  расставлены  тонкие  перегородки  с  отверстием  радиуса  ,    равно  отношению  площадей  ,  где  ,  поскольку  распределение  частиц  в  сечении  в  этом  случае  равномерно.  Наличие  узкого  участка  к  обеднению  вероятности  нахождения  частиц  на  стенке,  что  учитывается  введением  фактора  ,  где  ,  причем  этот  фактор  равен  1  только  при  .  Как  показано  в  [6],  .  С  учетом  приведенных  соображений  находится  искомая  вероятность  пребывания  частицы  в  подвижном  состоянии  и  в  результате  эффективная  подвижность  может  быть  записана  в  виде

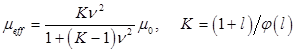  .  (1)

Рисунок  2  показывает  хорошее  согласие  предсказаний  (1)  с  данными  моделирования.

Переходя  к  вычислению    заметим,  что  вклад  в  продольную  диффузию  связан  с  двумя  факторами:  средним  временем,  проводимым  частицей  в  подвижном  состоянии,  ,  и  дисперсией  этого  времени  ,  где    —  время  наблюдения.  Соответственно,  при      может  быть  записан  в  виде  [6]  (–  коэффициент  свободной  диффузии)

  (2)

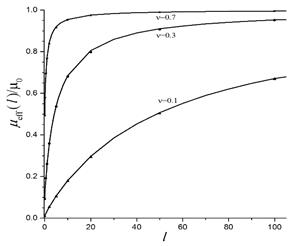
Рисунок  2.  Отношение  подвижностей    как  функция    при  значениях  ,  ,  и    Символами  представлены  результаты  для  ,  полученные  на  основании  данных  компьютерного  моделирования  с  .  Сплошные  кривые  получены  из  формулы  (1)

Отношение    при  .  Для  вычисления  дисперсии    удобно  воспользоваться  методом,  предложенным  в  [1]  для  нахождения  дисперсии  времени  пребывания  в  круге  радиуса    частицы,  блуждающей  в  круге  радиуса  .  Повышение  вероятности  пребывания  частицы  в  малом  круге  (за  счет  наличия  узкого  участка  трубки)  мы  учитываем,  вводя  в  него  потенциальную  яму,  глубина  которой    зависит  как  от  длины  узкого  сегмента,  так  и  от  фактора  .  Обобщая  таким  образом  результат  [1],  получим  из  (2)  следующее  выражение

  .  (3)

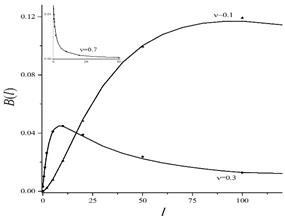
Рисунок  3.  Параметр  ,  характеризующий  ,  как  функция    при  значениях  ,    и  .  Символами  представлены  результаты,  полученные  на  основании  данных  моделирования,  при  .  Сплошные  кривые  отвечают  формуле  (3)

Рисунок  3  показывает  хорошее  согласие  предсказаний  (1)  с  данными  моделирования.  Перескоки  между  состояниями  приводят  к  квадратичному  по  силе  слагаемому.  Поскольку  наш  подход  оправдан  при  ,  это  слагаемое,  как  правило,  доминирует,  то  есть  .  Только  при  ,  когда  вариация  сечения  мало  значима,  доминирует  второе  слагаемое  в  (3)  и  .  Пока    зависимость  ,  проходит  через  максимум.  При    коэффициент  диффузии  с  ростом    монотонно  снижается  вплоть  до  . 

Таким  образом,  для  сложной  модели  удалось  найти  транспортные  коэффициенты  частицы,  характеризующие  ее  дрейф  и  диффузию  в  условиях  сильного  сноса.  Предложенный  подход  основан  на  замене  стационарного  неравновесного  состояния  3D  задачи,  равновесным  состоянием  2D  задачи.  Его  оправданность  доказана  сопоставлением  предсказаний  теории  с  данными  численного  моделирования,  выполненного  методом  3D  броуновской  динамики.  Хотя  полученные  результаты  справедливы  лишь  при  ,  наличие  оценок  и  при    [5]  позволяет  надеяться  на  возможность  построения  интерполяций,  применимых  при  любой  силе  поля.

Список  литературы:

1.Berezhkovskii  A.M.  Variance  of  residence  time  spent  by  diffusing  particle  in  a  sub-domain:  Path  integral  based  approach.  //  Chem.Phys.  —  2010.  —  V.  370.  —  №  1—3.  —  P.  253—257.

2.Berezhkovskii  A.M.,  Dagdug  L.,  Makhnovskii  Yu.A.,  Zitserman  V.Yu.  Drift  and  diffusion  in  a  tube  of  periodically  varying  diameter.  Driving  force  induced  intermittency  //  J.  Chem.  Phys.  —  2010.  —  V.  132.  —  №  22.  —  Ar#  221104.

3.Jacobs  M.H.  Diffusion  Processes.  Springer-Verlag  New  York  Inc.,  1967.  —  160  p.

4.Makhnovskii  Yu.A.,  Berezhkovskii  A.M.,  Bogachev  L.V,  Zitserman  V.Yu.  Driven  diffusion  in  a  periodically  compartmentalized  tube:  Homogeneity  versus  intermittency  of  particle  motion.  J.  Phys.  Chem.  B.  —  2011.  —  V.  115.  —  №  14.  —  P.  3992—4002.

5.Makhnovskii  Yu.A.,  Berezhkovskii  A.M.,  Zitserman  V.Yu.  Diffusion  in  a  tube  of  alternating  diameter.  //  Chem.  Phys.  —  2010.  —  V.  367.  —  №  2/3.  —  P.  110—114.

6.Zitserman  V.Yu.,  Berezhkovskii  A.M.,  Antipov  A.E.,  Makhnovskii  Y.A.  Biased  diffusion  in  tubes  of  alternating  diameter:  Analytical  treatment  in  the  case  of  strong  bias.  //  J.  Chem.  Phys.  —  2014.  —  V.  141.  —  №  21.  Ar#  214103.