МОДЕЛИРОВАНИЕ  ПРОЦЕССОВ  СОПРОВОЖДЕНИЯ  ДЕЯТЕЛЬНОСТИ  ОБРАЗОВАТЕЛЬНОГО  УЧРЕЖДЕНИЯ

Деменкова  Екатерина  Алексеевна

канд.  техн.  наук,  доцент  САФУ  имени  М.В.  Ломоносова,  РФ,  г.  Архангельск

Е-mail :  e.demenkova@narfu.ru

Бобров  Дмитрий  Александрович

студент  САФУ  имени  М.В.  Ломоносова,  РФ,  г.  Архангельск

Е-mail :  dmitry.b@live.com

SIMULATION  OF  SUPPORT  ACTIVITIES  OF  EDUCATIONAL  INSTITUTIONS

Ekaterina  Demenkova

candidate  of  engineering  sciences ,  associate  professor  of  NArFU,  Russia,  Arkhangelsk

Dmitry  Bobrov

student  of  NArFU,  Russia,  Arkhangelsk

АННОТАЦИЯ

Предложена  математическая  модель  процессов  сопровождения  деятельности  образовательного  учреждения,  разработанная  на  основе  аппарата  теории  полихроматических  множеств.

ABSTRACT

A  mathematical  model  of  the  processes  support  the  activities  of  the  educational  institution,  developed  on  the  basis  of  the  theory  of  polychromatic  sets.

Ключевые  слова :  математическая  модель;  производственные  процессы;  теория  полихроматических  множеств.

Keywords:  mathematical  model;  production  processes;  the  theory  of  polychromatic  sets.

Для  повышения  эффективности  функционирования  любой  организации  на  современном  этапе  развития  науки  и  техники  применяется  автоматизация  производственных  процессов.  Применение  таких  систем  позволяет  автоматизировать  процесс  поддержки  принятия  решений  в  различных  ситуациях,  избавляет  сотрудников  от  выполнения  рутинных  операций,  упрощает  ведение  учета,  хранения  и  обработки  данных  различной  природы,  организует  внутренний  документооборот,  автоматизирует  выполнение  расчетов,  формирование  отчетов  и  многое  другое.

Особенностью  автоматизации  процессов  в  сфере  образования  является  тот  факт,  что  среди  образовательных  учреждений,  помимо  университетов,  колледжей  и  образовательных  школ,  существуют  различные  специализированные  учебные  заведения,  учреждения  дополнительного  образования.  К  разным  видам  учреждений  требуется  индивидуальный  подход  с  изучением  соответствующей  нормативной  базы,  а  так  же  рассмотрение  внутренних  и  внешних  потоков  информации,  применение  современных  подходов  проектирования  систем.  Использование  же  автоматизированных  систем  позволяет  повысить  качество  предоставляемых  услуг  сотрудниками  детских  образовательных  центров  (ДОЦ),  сократит  риск  появления  ошибок.

Для  моделирования  информационных  процессов  сопровождения  деятельности  образовательного  центра  выберем  аппарат  теории  полихроматических  множеств. 

При  математическом  моделировании  производственных  процессов  сопровождения  деятельности  образовательного  учреждения  разрабатывается  производственная  система  Р,  которая  состоит  из  двух  составляющих: 

·     системы  технологических  операторов,  характеризующих  производственные  процессы  (процессы  документооборота  и  др.);

·     системы  информационных  объектов,  включающих  данные,  необходимые  для  реализации  технологических  операторов.

На  теоретико-множественном  уровне  состав  технологических  операторов  и  их  свойств  представляются  множествами  этих  элементов  и  их  персональных  цветов.  Свойства  производственной  системы  в  целом  представляются  множеством  унитарных  цветов.  Множества  технологических  операторов,  их  персональных  цветов  и  унитарных  цветов  моделируют  структуру  производственного  процесса.  Так,  состав  элементов  технологического  процесса  системы  сопровождения  деятельности  образовательного  учреждения  описывается  множеством

T  =  (t₁,  ...,  t_i,  ...,  t_n) ,    (1)

где  элементы  множества  описывают  операции  технологического  процесса  сопровождения  деятельности  образовательного  учреждения  в  системе.  Такими  операциями,  например,  являются  формирование  групп,  подготовка  договора  и  др.

Информационные  объекты,  необходимые  для  реализации  процессов  сопровождения  деятельности  образовательного  учреждения,  описываются  множеством  П,  множеством  их  персональных  цветов

П  =  (π₁,  …,  π  _j,…,  π  _m)                                    (2).

Для  процессов  представленной  системы,  элементами  множества  П  будут  персональные  данные  обучающегося,  данные  законного  представителя  обучающегося,  выбранное  объединение  и  др.

Полный  состав  элементов  системы  сопровождения  деятельности  образовательного  учреждения  описывается  множеством

Р  =  Т  È  П                                                        (3).

Отношения  смежности,  порядка  или  иерархической  подчиненности  между  элементами  всей  технологической  системы  Р  описываются  с  помощью  булевой  матрицы  [Р  х  Р],  которая  представляется  в  виде  блочной  матрицы

В  этой  матрице  блоки  [Т  х  Т]  и  [П  х  П]  описывают  бинарные  отношения  между  элементами  одного  множества,  задающего  технологические  операции  сопровождения  деятельности  образовательного  учреждения  Т  или  информационные  объекты  П.  Блоки  [Т  х  П]  и  [П  х  Т]  описывают  бинарные  отношения  между  t_i  Π T  и  π  _j  Π П,  т.  е.  определяют  необходимые  для  процесса  сопровождения  информационные  объекты  и  наоборот.

Для  установления  отношений  и  связей  между  свойствами  модели  производственной  системы  сопровождения  деятельности  образовательного  учреждения  Р  используется  пространство  контуров  F,  единой  для  всех  элементов  машины  и  производственной  системы  контроля.

F  =  (F ₁,  …,  F_N),  "F(Ai),  F(P)  (F(A_i),  F(P)  Í  F)                     (5)

Пространство  контуров  F  представляется  как  булево  векторное  пространство,  в  котором  составы  контуров  технологических  операторов  модели  сопровождения  деятельности  образовательного  учреждения  и  других  элементов  производственной  системы  представлены  булевыми  векторами  в  пространстве  (5).  Составы  контуров  технологических  операторов  и  информационных  объектов  представляются  матрицами  контуров 

||  c_i(j)  ||_{T,  F(T)}  =  [T  x  F(T)],                                           (6)

||  c_i(j)  ||_{П,  F(П)}  =  [П  x  F(П)],                                         (7)

а  составы  контуров  элементов  производственной  системы  в  целом  описываются  булевой  матрицей  контуров

||  c_i(j)  ||_{P,  F(P)}  =  [P  x  F(P)]                                           (8)

Процесс  сопровождения  деятельности  образовательного  учреждения  моделируется  в  виде  технологического  процесса  T_i  как  упорядоченной  последовательности  технологических  операторов

T_i  =  (t_{i  1},   t_{i  2},  …,  t_{i  k-1},  t_{i  k},  …,  t_{i  n}),                                (9)

воздействующих  на  модель  функционирования  по  основному  назначению  А_i  и  осуществляющих  преобразование  этой  модели  из  предшествующего  (A_i)_k-1  в  последующее  (A_i)_k  состояние.  При  этом  принимается  F(T)  =  F(P).

Состав  контуров  производственной  системы  восстановления  работоспособности,  взаимодействующей  с  контурами  объектов  восстановления,  равен

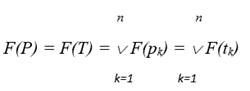                  (10)

Исходной  информацией  выступает  вектор  VLi   (i  =  1..K)  с  набором  определенных  значений.  Тот  компонент  вектора,  который  имеет  нулевое  значение  и  нуждается  в  реализации.  Вектор  VLi  может  иметь  не  одно,  а  несколько  нулевых  значений.

Сопроводительные  процессы  могут  комбинироваться  в  группы,  например,  необходимость  учета  нескольких  свойств  при  формировании  отчета  и  др.  Поэтому  связь  между  элементами  модели  дизъюнктивная.

При  дизъюнктивной  форме  связи  контуров  производственных  процессов  А  и  модели  производственной  системы  сопровождения  деятельности  образовательного  учреждения  для  преобразующего  контура  F_j (t_k)  оператора,  взаимодействующего  с  контуром  F_j(А)  основного  процесса,  принимаются  следующие  логические  значения:  F_j(t_k)  =  1,  если  оператор  t_k  реализует  контур  F_j(А),  и  F_j(t_k)  =  0  –  в  противном  случае.

На  основе  математической  модели  разработаны  функциональные  модели  с  использованием  методологии  SADT,  на  основе  которых  разработана  логическая  модель  системы  автоматизации  процессов  сопровождения  деятельности  образовательного  учреждения.  Фрагмент  модели  приведен  на  рисунке  1.

Таким  образом,  для  моделирования  производственных  процессов  образовательного  учреждения  необходимо  выделить  три  составляющие:

1.  модель  процессов  ведения  образовательной  деятельности  А  (основная  деятельность  по  предназначению);

2.  модель  процессов  сопровождения  деятельности  образовательного  учреждения  Р  (подготовка  договоров,  отчетов  и  др.),  которая  в  свою  очередь  состоит  из:

·     системы  технологических  операторов,  характеризующих  производственные  процессы  Т  (процессы  документооборота  и  др.);

·     системы  информационных  объектов,  включающих  данные,  необходимые  для  реализации  технологических  операторов  П.

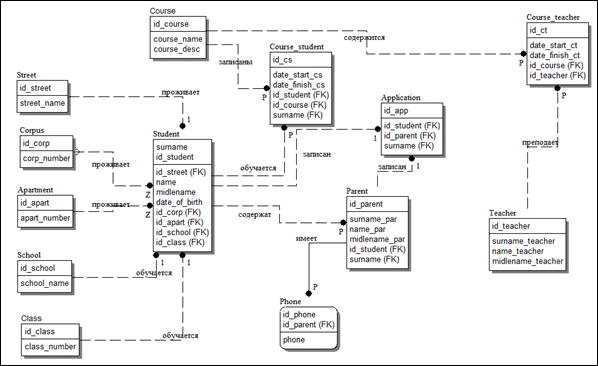
Рисунок  1.  Логическая  модель  данных,  построенная  на  основе  математической  модели

Список  литературы:

1.Павлов  В.В.  Структурное  моделирование  в  CALS-технологиях/  В.В.  Павлов;  [отв.ред.  Ю.М.  Соломенцев];  Ин-т  конструкторско-технологической  информатики  РАН.  М.:  Наука,  2006.  —  307  с.

2.Павлов  В.В.  CALS-технологии  в  машиностроении  (математические  модели).  Под  редакцией  Ю.М.  Соломенцева.  М.:  ИЦ  МГТУ  СТАНКИН,  2002.  —  с.  328.