Статья опубликована в рамках: XXVI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 12 января 2015 г.)
Наука: Химия
Секция: Физическая химия
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ДИФФУЗИОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЕГИДРИРОВАНИЯ ИЗОАМИЛЕНОВ В ИЗОПРЕН НА НЕПОДВИЖНОМ ЖЕЛЕЗОКАЛИЕВОМ КАТАЛИЗАТОРЕ
Уртяков Петр Владимирович
аспирант, Казанский Приволжский Федеральный Университет, РФ, г. Казань
E-mail:
A DIFFUSION MATHMATICAL MODEL FOR THE DEHYDROGENATION OF ISOAMYLENES TO ISOPRENE USING A FIXED BED IRON–POTASSIUM CATALYSTS
Urtyakov Petr
post graduate student, Kazan State University, Russia, Kazan
АННОТАЦИЯ
Предложена математическая модель процесса дегидрирования изоамиленов в изопрен на неподвижных промышленных саморегенерирующихся железокалиевых катализаторах, которая учитывает размер и форму зерен катализатора, степень их закоксованности, коэффициент диффузии, скорость и энергию активации прямой (дегидрирование) и обратной (гидрирование) реакции, реакций крекинга и саморегенерации. Математическая модель позволяет адекватно описать физико-химические процессы для различных режимных параметров эксплуатации реактора.
ABSTRACT
A mathematical model of the process of dehydrogenation of isoamylenes in isoprene on fixed-bed industrial self-recovering Iron–Potassium catalysts. Model takes into account the size and shape of the catalyst grains, the degree of coking, the diffusion coefficient, rate and activation energy of direct (dehydrogenation) and reverse (hydrogenation) reaction, cracking reactions and self-regeneration. The mathematical model adequately describe the physical and chemical processes for the various conditions of operation of the reactor.
Ключевые слова: Дегидрирование изоамиленов; изопрен; математическая модель; диффузия.
Keywords : Mathematical model; dehydrogenation of isoamylenes; isoprene; diffusion.
Введение
Процесс дегидрирования изоамиленов в изопрен в промышленных условиях, как правило, осуществляется в адиабатических реакторах со стационарным слоем катализатора. Для понимания физико-химической сущности процесса дегидрирования, определения условий его промышленной реализации и последующей оптимизации режимов эксплуатации химического реактора необходимо разработать его математическую модель.
В настоящей работе развивается предложенная в [2] диффузионная модель процесса дегидрирования на примере железокалиевого катализатора. Среди вторичных реакций в математической модели выделяются две наиболее существенные: разложение изоамиленов и изопрена с образованием углеводородов, углекислого газа и кокса, и реакция саморегенерации — очищение катализатора от кокса. Это позволило описать распределение физических характеристик и концентраций основных компонент реакционной смеси в реакторе (изоамиленов, изопрена, водорода, продуктов крекинга и углекислого газа), а также определить степень закоксованности катализатора.
Описание физическо-химических процессов
Процесс дегидрирования изоамиленов осуществляется в адиабатических реакторах со стационарным слоем катализатора. Реакция дегидрирования является эндотермической, обратимой и сопровождается увеличением объема вследствие выделения водорода. Дегидрирование изоамиленов проводят в присутствии водяного пара с целью подвода тепла в зону реакции, снижения парциального давления водорода [5] и удаления с поверхности катализатора продуктов олигомеризации путем их газификации [6].
Зернистый слой реактора представляет собой бипористую среду. Эта среда составлена из зерен — гранул катализатора, в свою очередь также имеющих пористую структуру. Реакционные компоненты и тепло за счет диффузионного и теплового потоков поступают из гранул катализатора в межзерновое поровое пространство, где проходит основной фильтрационный поток.
В математической модели учитываются реакция дегидрирования изоамиленов в изопрен:
![]() , (1)
, (1)
крекинг изоамиленов и изопрена
![]()
 (2)
(2)
реакция саморегенерации
![]() . (3)
. (3)
Через Q, кДж/моль, обозначено количество теплоты, поглощающееся в результате реакции. Здесь CncHnh — продукты крекинга, химический состав (коэффициенты nc, nh) которых, а также стехиометрические коэффициенты ![]() , i=1,2,3, j=1,2 в ходе адаптации моделиприняли следующие значения: nc=2,5, nh=4,6,
, i=1,2,3, j=1,2 в ходе адаптации моделиприняли следующие значения: nc=2,5, nh=4,6, ![]() =1,09,
=1,09, ![]() =1,7,
=1,7, ![]() =0,75,
=0,75, ![]() =0,09,
=0,09, ![]() =1,7,
=1,7, ![]() =0,75.
=0,75.
Математическая модель
Разрабатываемая в данной работе математическая модель расщепляется на две взаимосвязанные подмодели. Первая из них (внешняя) описывает процессы фильтрации и тепломассопереноса в межзерновом поровом пространстве. Вторая (внутренняя) — диффузию и химические реакции внутри зерен катализатора. Внешняя служит для нахождения вектора массовых концентраций компонент x = (x1, x2, x3, x4, x5), кг/кг, реакционной смеси, температуры T, K, и давления p, Па, в межзерновом поровом пространстве. Индексами i = 1...5 здесь обозначены компоненты в следующем порядке: изоамилены, изопрен, водород, продукты крекинга, углекислый газ. В стационарном случае все эти величины зависят лишь от координаты z, м, вдоль оси реактора. Внутренняя задача служит для нахождения вектора массовых концентраций компонент X = (X1, X2, X3, X4, X5), кг/кг, внутри гранулы катализатора. Компоненты этого вектора зависят как от положения z гранулы внутри реактора, так и от пространственной координаты r, м, отсчитываемой от центра гранулы к ее поверхности.
Для решения внешней задачи необходимо знать кажущиеся скорости реакции w(z), моль/м3с, обеспечивающие поступление (отбор) в реакционную смесь ее компонент. Кажущиеся скорости определяются через диффузионные потоки компонент из зерна и являются функционалами от вектора X(z,r). Наоборот, определение X(z,r) требует знания концентраций x(z), а также температуры T(z) и давления p(z) на поверхности гранулы, от которых зависят истинные скорости реакции. Температуру и давление, как было оговорено выше, можно считать постоянными внутри гранулы. Указанные взаимосвязи подмоделей и общая структура математической модели представлена на рис. 1.
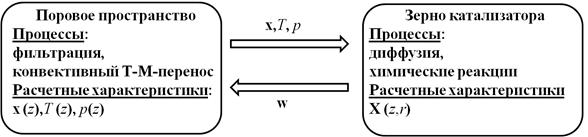
Рисунок 1. Общая структура математической модели
Рассмотрим более подробно внешнюю подмодель. Приняв схему реактора идеального вытеснения, получим для распределения концентраций реагентов вдоль реактора следующие дифференциальные уравнения
![]() , (4)
, (4)
с граничными условиями
![]() ,
, ![]() ,
,
где: S — площадь поперечного сечения реактора, м2;
G — массовый расход сырья, кг/с;
Mi — молярная масса i-го газового компонента, кг/моль;
![]() — массовые концентрации компонент на входе в реактор, кг/кг;
— массовые концентрации компонент на входе в реактор, кг/кг;
Ui , моль/м3с, — производство i-го компонента в единице объема реактора в единицу времени.
Рассмотрим внутреннюю подмодель. Для удобства перейдем к мольным концентрациям Ci, ci, i=1…5 моль/м3, компонент в газе, которые связаны с их массовыми концентрациями Xi, xi, i=1..5 в реакционной смеси внутри зерна и в межзерновом пространстве формулами
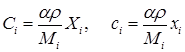
где: ρ, кг/м3, — плотность газа.
Распределение компонентов внутри зерна описывается стационарными уравнениями диффузии:
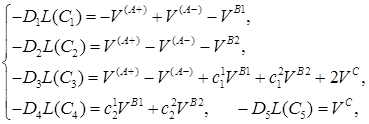 (5)
(5)
где: Di, м2/с, — эффективный коэффициент диффузии i-го компонента,
L — оператор Лапласа. Фигурирующие в правых частях уравнений (5) истинные скорости реакций V(A+), V(A-), VB1, VB2, VC, моль/м3с, определяются как количество молей, реагирующих за единицу времени в единице объема гранулы в реакциях дегидрирования (прямой и обратной), крекинга (изоамиленов и изопрена) и саморегенерации.
Для конкретизации задачи зададим зависимости скоростей реакций V(A+), V(A-), VB1, VB2, VC от концентраций компонентов, температуры T и давления p:
 (6)
(6)
Функции k+(T), kcr1(T), kcr2(T), kreg(T), 1/с, Ca(T,p), моль/м3, определяются по формулам
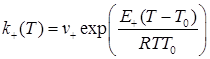 ,
,
 ,
,
 ,
,
 ,
,
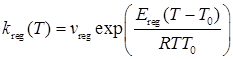 ,
,
где: R = 8.31 Дж/моль∙К — универсальная газовая постоянная;
p -, Па, — константа равновесия основной реакции;
ν +, νcr1, νcr2, νreg, 1/с, — константы скоростей, а E+, E-, Ecr1, Ecr2, Ereg,, Дж/моль, — энергии активации реакций,
C пар, моль/м3, — мольная концентрация паров воды в газовом объеме внутри зерна.
Параметр φ представляет собой долю свободных активных центров, которую при описании промышленных данных мы будем считать установившейся. В этом случае она выражается через концентрации изоамиленов и изопрена:
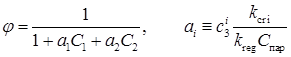 . (7)
. (7)
Система уравнений (5)—(7) представляет собой внутреннюю подмодель, описывающую процессы в гранулах катализатора. Она служит для нахождения распределения в грануле мольных концентраций газовых компонент Ci(z,r) и степени закоксованности катализатора φ(z,r).
Оценка работы реактора проводится по коэффициентам ВП, % масс, — выход целевого продукта в расчете на пропущенное сырье и ВР, % масс, — выход целевого продукта в расчете на разложенное сырье, определяемым по концентрациям изоамиленов и изопрена
 ,
,  .
.
В работе представлен общий вид модели, однако то, в каких пропорциях участвуют в реакции крекинга изоамилены и изопрен, доподлинно неизвестно. Поэтому, в процессе исследований, для определенности, рассматривались две альтернативные модели, предполагающие преимущественный крекинг изопрена или изоамиленов. Второй вариант модели оказался более предпочтительным ввиду лучшего качества описания, как лабораторных экспериментов, так и результатов эксплуатации промышленных реакторов, с помощью одинакового набора параметров математической модели. Поэтому далее все результаты будут приведены именно для варианта модели, предполагающего отсутствие крекинга изопрена.
Адаптация и тестирование модели
Представленная математическая модель включает одиннадцать адаптационных параметров: D, ν+, E+, p-, E-, νcr, Ecr, νreg, Ereg, γ, Q. Их нахождение производилось методом подбора с целью наилучшего описания фактических данных для каждого типа катализатора.
В качестве примера описания лабораторных данных рассмотрим испытания катализатора КДО, при которых использовалось 40 см3 фракции катализатора диаметром 2-3 мм. Полученные в результате анализа лабораторных данных значения искомых параметров модели представлены в таблице 1. Здесь G0, ч-1, — объемная скорость подачи сырья, связанная с массовым расходом G формулой
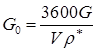 ,
,
где: V — объем реактора,
ρ * = 650 кг/м3 — плотность сырья при нормальных условиях.
Из представленных данных можно сделать вывод о хорошем качестве описания математической моделью зависимости выходных характеристик от температуры и нагрузки по сырью.
Таблица 1.
Экспериментальные и теоретические данные по активности и селективности
|
№ |
M |
T, oC |
G0, ч-1 |
ВПэксп |
ВПтеор |
ВРэксп |
ВРтеор |
|
1 |
5.2 |
600 |
1 |
49.8 |
49.68 |
89.47 |
89.5 |
|
2 |
5.2 |
610 |
1 |
53.3 |
53.22 |
88.7 |
88.49 |
|
3 |
5.2 |
615 |
1 |
54.5 |
54.8 |
87.5 |
87.9 |
|
4 |
5.2 |
625 |
1 |
57.3 |
57.54 |
87 |
86.6 |
|
5 |
5.2 |
615 |
1 |
54.1 |
54.8 |
87.4 |
87.9 |
|
6 |
5.2 |
600 |
1 |
49.8 |
49.68 |
89.47 |
89.5 |
|
7 |
5.2 |
600 |
0.75 |
52.6 |
52.64 |
88.4 |
88.3 |
|
8 |
5.2 |
600 |
0.55 |
53.6 |
53.73 |
87.2 |
86.45 |
|
9 |
5.2 |
600 |
0.75 |
52.7 |
52.64 |
88.5 |
88.32 |
|
10 |
5.2 |
600 |
1 |
49.8 |
49.68 |
89.47 |
89.5 |
|
11 |
5.2 |
600 |
1.25 |
45.3 |
46.25 |
90 |
90.15 |
|
12 |
5.2 |
600 |
1.35 |
43.9 |
44.89 |
92.1 |
90.34 |
Для оценки погрешности описания промышленных данных рассмотрим работу реакторов проточного типа на 8, 17 и 50 тонн катализатора, использовавшихся для производства изопрена в ОАО «Нижнекамскнефтехим».
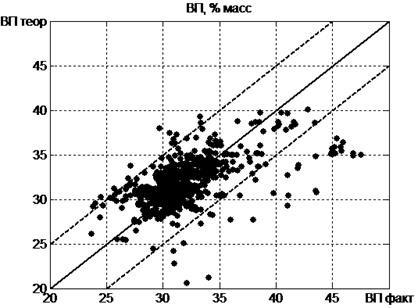
Рисунок 2. Сравнение теоретических и фактических данных по ВП для промышленных реакторов
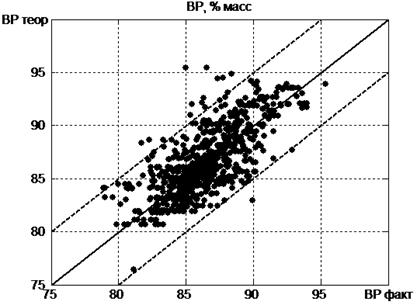
Рисунок 3. Сравнение теоретических и фактических данных по ВР для промышленных реакторов
На рисунках 2, 3 точками изображены пары значений (ВП факт, ВП теор) и (ВР факт, ВР теор) в соответствующей плоскости для реакторов. Идеальному соответствию теории с экспериментом отвечает прямая, проходящая через нуль с единичным наклоном. На рисунке она изображена сплошной линией. Пунктирные линии отвечают отклонению теории от эксперимента на 5 % масс. Как видно из представленных на рис. 2, 3 данных согласие теории с экспериментом оказывается хорошим для всех трех рассмотренных реакторов. Небольшое количество точек, лежащих в нижней части рисунков обусловлено фактическими данными за 1—2 дня, следующими за датами регенерации катализатора в реакторе. Они в принципе не могут быть описаны в рамках данной квазистационарной модели.
Выводы
1. Предложена и адаптирована по лабораторным и промышленным данным математическая модель дегидрирования изоамиленов в реакторах с неподвижным слоем катализатора, учитывающая размер гранул катализатора и степень его закоксованности, эффективный коэффициент диффузии, константы скоростей и энергии активации основной реакции, реакции крекинга и саморегенерации, накопление невымываемого кокса.
2. Предложенная модель способна описать имеющийся обширный фактический материал по эксплуатации промышленных адиабатических реакторов проточного типа с неподвижным слоем катализатора.
3. Установлено, что предположение о преимущественном крекинге изоамиленов позволяет более качественно описать на основе математической модели известные факты.
4. Измеренные в лаборатории скорость реакций дегидрирования и крекинга изоамиленов, положение равновесия и энергии активации прямой и обратной ветви основной реакции можно непосредственно использовать при моделировании работы промышленных реакторов.
Список литературы:
1.Боресков Г.К. Гетерогенный катализ М.: Наука, 1986.
2.Егоров А.Г., Ламберов А.А., Дементьева Е.В., Уртяков П.В. О диффузионной модели процесса дегидрирования изоамиленов в изопрен с использованием железокалиевых катализаторов // Катализ в промышленности. — 2011. — № 5. — С. 54.
3.Ивашкина Е.Н., Францина Е.В., Романовский Р.Е., Долганов И.М., Иванчина Э.Д., Кравцов А.В. Разработка методики увеличения ресурса работы катализатора дегидрирования высших парафинов на основе нестационарной кинетической модели реактора // Катализ в промышленности. — 2012. — № 1. — С. 40.
4.Краснов К.С., Воробьев Н.К., Годнев И.Н. и др. Физическая химия. М.: Высш. шк., 2001.
5.Крылов О.В. Гетерогенный катализ: Учебное пособие для вузов / О.В. Крылов М.: ИКЦ «Академкнига», 2004.
6.Meima G.R. Catalyst deactivation phenomena in styrene production / R.G. Meima, M. Govind // Applied Catalysis A: General. — 2001. — Vol. 212. — Р. 239.
дипломов


Оставить комментарий