Статья опубликована в рамках: XXVI Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 12 января 2015 г.)
Наука: Информационные технологии
Секция: Математическое моделирование, численные методы и комплексы программ
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ЗАДАЧА ОПРЕДЕЛЕНИЯ ЧАСТОТ СВОБОДНЫХ КОЛЕБАНИЙ РОТОРА С ГИРОСКОПИЧЕСКИМ ГАСИТЕЛЕМ
Сафина Гульнара Фриловна
канд. физ.-мат. наук, доцент Нефтекамского филиала БашГУ, РФ, г. Нефтекамск
PROBLEM OF DETERMINATION OF FREQUENCIES OF FREE FLUCTUATIONS OF THE ROTOR WITH THE GYROSCOPIC QUENCHER
Gulnara Safina
candidate of physical.-a mat. sciences, associate professor of Neftekamsk branch of BashGU, Russia, Neftekamsk
АННОТАЦИЯ
В работе исследована прямая задача определения частот свободных колебаний ротора с гироскопическим гасителем. Получено частотное уравнение свободных колебаний ротора с гасителем. Показан пример определения частот четырех нормальных форм колебаний ротора.
ABSTRACT
In work the direct problem of determination of frequencies of free fluctuations of a rotor with a gyroscopic quencher is investigated. The frequency equation of free fluctuations of a rotor with a quencher is received. The example of determination of frequencies of four normal forms of fluctuations of a rotor is shown.
Ключевые слова: прямая задача; ротор с гироскопическим гасителем; частоты свободных колебаний; частотное уравнение.
Keywords: direct task; a rotor with a gyroscopic quencher; frequencies of free fluctuations; frequency equation.
Рассмотренная задача определения частот свободных колебаний ротора с гироскопическим гасителем относится к исследованиям спектральных задач свободных колебаний механических систем и их составляющих. Подобные исследования с валами с дисками, валами на опорах, жестким ротором на податливых подшипниках, лопатками турбины с бандажом проведены, например, в работах [2]—[4]. В данной же работе рассматриваются свободные колебания ротора с гироскопическим виброгасителем.
Известно, что колебания могут непосредственно угрожать прочности механической системы, постепенно подготавливая ее усталостное разрушение. В таких случаях исследования в спектральных задачах свободных колебаний механических систем могут указать пути для уменьшения вредных колебаний.
Рассмотрим свободные колебания, возникающие при вращении вала [1] с инструментальной оправкой и гироскопическим виброгасителем (рисунок 1). Действие виброгасителя основано на гироскопическом эффекте, возникающем при перемещении оси вращения ![]() вала оправки 1 вследствие ее свободных или вынужденных колебаний в положение
вала оправки 1 вследствие ее свободных или вынужденных колебаний в положение ![]() .
.
За обобщенные координаты примем координаты точки ![]()
![]() и угловые координаты — углы Эйлера-Крылова:
и угловые координаты — углы Эйлера-Крылова: ![]() — угол между осью вала
— угол между осью вала ![]() и проекцией на плоскость
и проекцией на плоскость ![]() ;
; ![]() — угол между осью вала
— угол между осью вала ![]() и проекцией на плоскость
и проекцией на плоскость ![]() .
.
Уравнения колебательного процесса такой механической системы получим энергетическим методом с помощью уравнений Лагранжа, которые примут вид:
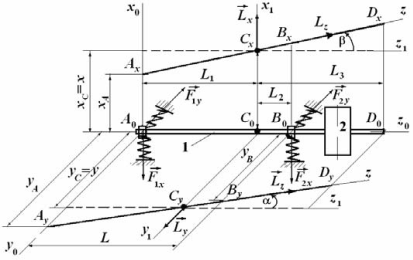
Рисунок 1. Схема упругого подвеса оправки с виброгасителем; 1 — вал оправки (ротор), 2 — маховик с приводом
|
|
(1) |
Здесь ![]() и
и ![]() — функции кинетической и потенциальной энергии ротора. Абсолютную угловую скорость ротора и ее проекции на оси
— функции кинетической и потенциальной энергии ротора. Абсолютную угловую скорость ротора и ее проекции на оси ![]() представим в виде:
представим в виде:
|
|
(2) |
где: ![]()
![]() — углы Эйлера-Крылова, характеризующие повороты ротора соответственно вокруг
— углы Эйлера-Крылова, характеризующие повороты ротора соответственно вокруг ![]() и
и ![]() , связанные с вращающимся ротором.
, связанные с вращающимся ротором.
На основании теоремы Кенинга и с учетом (2) функции кинетической и потенциальной энергии ротора примут вид:
|
|
(3) |
В последних равенствах (3): ![]() — масса и главные центральные моменты инерции ротора;
— масса и главные центральные моменты инерции ротора; ![]() и
и ![]() — коэффициенты жесткости упругих опор
— коэффициенты жесткости упругих опор ![]() и
и ![]() ротора;
ротора; ![]() — расстояние между опорами
— расстояние между опорами ![]() и
и ![]() ,
, ![]() — расстояние от центра масс
— расстояние от центра масс ![]() до опоры
до опоры ![]() ,
, ![]() — расстояние от центра масс
— расстояние от центра масс ![]() до опоры
до опоры ![]() ;
; ![]() — угловая скорость собственного вращения ротора вокруг оси
— угловая скорость собственного вращения ротора вокруг оси ![]() .
.
Подставляя выражения функций кинетической и потенциальной энергии ротора и их производных в систему уравнений (1) получим следующую систему дифференциальных уравнений:
|
|
(4) |
Уравнения системы (4) полностью описывают свободные колебания ротора с гироскопическим виброгасителем.
Учтем теперь, что ротор с виброгасителем совершает свободные гармонические колебания и примем решения системы (4) в виде:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
где: ![]() — частота,
— частота,
![]() ,
,![]() ,
,![]() ,
,![]() — амплитуды свободных колебаний ротора. Подставляя решения и их производные в систему уравнений (4) получим следующую систему алгебраических уравнений относительно амплитуд:
— амплитуды свободных колебаний ротора. Подставляя решения и их производные в систему уравнений (4) получим следующую систему алгебраических уравнений относительно амплитуд:
|
|
(5)
|
Система уравнений (5) будет иметь ненулевое решение относительно ![]() ,
,![]() ,
,![]() ,
,![]() в случае нулевого определителя этой системы. Приравнивая определитель системы (5) к нулю, получим частотное уравнение:
в случае нулевого определителя этой системы. Приравнивая определитель системы (5) к нулю, получим частотное уравнение:
|
|
(6) |
в котором коэффициенты ![]()
![]()
![]()
![]()
![]() выражаются через физические параметры системы:
выражаются через физические параметры системы:
![]() ;
;
![]()
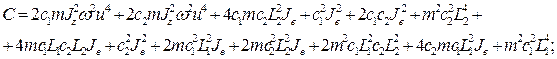
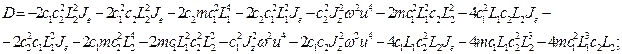
![]()
Из частотного уравнения (6) при известных физических параметрах ротора с виброгасителем можно определить частоты четырех нормальных форм колебаний ротора.
Решение прямой задачи рассмотрим на примере. Определим собственные частоты колебаний ротора виброгасителем, для которого известны следующие физические параметры [1]:
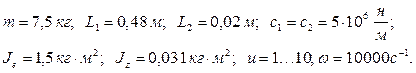
Частотное уравнение (7) после подстановки в него заданных физических параметров принимает вид:
![]()
Решение последнего уравнения, найденное с помощью ЭВМ, следующее:
![]()
Следовательно, частоты колебаний ротора:
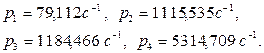
Список литературы:
1.Лапин А.Д. Резонансный поглотитель изгибных волн в стержнях и пластинах // Акустический журнал. — 2002. — № 2. — C. 277—280.
2.Сафина Г.Ф., Иванова Е.А. Диагностирование жесткостей опор ротора по частотам его свободных колебаний. // Физическое образование в вузах. — Т. 20. — № 1С. — 2014. — С. 33.
3.Сафина Г.Ф. Акустическое диагностирование характеристик лопаток турбины, связанных бандажом // Контроль. Диагностика — 2014. — № 7. — С. 64—72.
4.Сафина Г.Ф. Акустическое диагностирование механических систем. Ч. 1. Уфа: РИЦ БашГУ, 2013. — 109 с.
5.Сафина Г.Ф. Акустическое диагностирование механических систем: монография. В 2 ч. Ч. 2 Уфа: РИЦ БашГУ, 2014. — 110 с.
дипломов


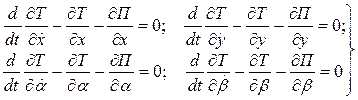 .
.
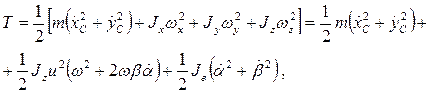
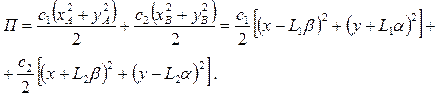
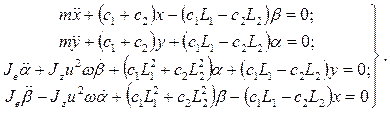
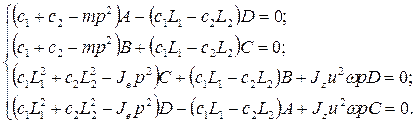
Оставить комментарий