МЕТОД  ДЛЯ  СГЛАЖИВАНИЯ  ИЗОБРАЖЕНИЙ  НА  ОСНОВЕ  ПОЛНОЙ  ВАРИАЦИИ

Данг  Нгок  Хоанг  Тхань

аспирант  Тульского  государственного  университет,  РФ,  г.  Тула

Email :  myhoangthanh@yahoo.com

Фан  Зуй  Тунг

магистрант  Тульского  государственного  университет,  РФ,  г.  Тула

Email: 

A  METHOD   TO  SMOOTH  IMAGE  BASED  ON  TOTAL  VARIATION

Dang  Ngoc  Hoang  Thanh

postgraduate  student  of  Tula  State  University,  Tula

Phan  Duy  Tung

graduate  student  of  Tula  State  University,  Tula

АННОТАЦИЯ

В  работе  предложен  один  метод  для  сглаживания  изображений.  Сглаживания  изображений  —  это  фильтрация  сигнала  от  ступенчатых  изменений.  В  этом  случае,  сигнал  является  двухмерным.  Мы  считаем,  что  идеальный  сигнал  не  содержит  таких  изменений.  Данный  метод  построен  на  основе  полной  вариации  [2].

ABSTRACT

In  this  paper  we  propose  a  method  to  smooth  images.  Image  smoothness  is  a  signal  filter  process  from  stepped  variations.  In  this  situation,  the  signal  is  two  dimensional.  We  consider  that  ideal  signal  doesn’t  include  these  variations.  This  method  is  based  on  total  variation.

Ключевые   слова:  сглаживание  изображения;  полная  вариация.

Keywords:  image  smoothness;  total  variation. 

Ступенчатый  сигнал  [1]  за  счёт  множества  резких,  но  небольших  по  амплитуде,  перепадов  уровня  содержит  высокочастотные  составляющие,  которых  нет  в  сглаженном  сигнале.  Поэтому  для  некоторого  алгоритма  сглаживания  в  первую  очередь  необходимо  определить  как  сильно  ослабляются  разные  частотные  составляющие.  Это  значит,  что  необходимо  построить  амплитудно-частотную  характеристику  соответствующего  фильтра.

Пусть  в  пространстве    задана  ограниченная  область  .  Пусть  каждая  точка    определена  своими  координатами  ,  где    и  .  Кроме  того,  пусть  каждая  точка    характеризуется  двумя  значениями  .

В  частности,  рассматривая  растровые  изображения,  мы  полагаем,  что  область    состоит  из  элементов    и  образует  прямоугольную  область  в  ,  где  ,    и    —  соответствующие  диапазоны  значений  координат.

В  этих  условиях  назовём    функцией  яркости  исходного  изображения,    —  функцией  яркости  реального  изображения.  Пусть    —  какое-то  семейство  гладких  функций.

Пусть  заданы  гладкая  функция    и  ограниченная  область  .  Тогда  полная  вариация    функции    имеет  вид  [1]:    где    и  .

Идеей  для  сглаживания  изображения  является  нахождение  оценки    функции    для  минимизации  ее  полной  вариации  [2]  но  не  изменяется  среднее  значение  яркости  всех  точек  изображения.  Это  значит,  что:

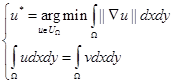.                                  (1)

Задача  (1)  соответствует  следующей  задаче:

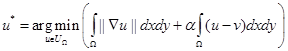,                    (2)

где:    —  множитель  Лагранжа.  Построим  уравнение  Эйлера-Лагранжа  задачи  (2):

,  ,

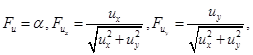
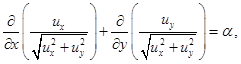                                 (3)

при  граничном  условии  .

Мы  можем  писать  уравнение  (3)  в  следующем  виде:

                                (4)

Для  решения  уравнения  (4),  можем  использовать  разностные  схемы  и  итерационные  методы.  Будем  решать  уравнение  (4)  при  ограничении    на  ,  итерационно  пересчитывая  значения  некоторой  функции  :

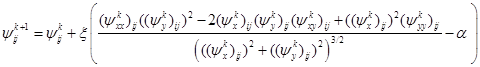,             (5)

где:

,,,  ,

при  граничном  условии  ;  где        ;    -  числа  точек  изображения  по  горизонтали  и  вертикали.

Процесс  (5)  при  граничном  условии    сходится,  и  принимаем  .  Результат  сглаживания  изображения  показывается  на  рис.  1.

Рисунок  1.  Результат  сглаживания  а)  Реальное  изображение  б)  Сглаживание 

Обратим  внимание  на  то,  что  мы  рассматриваем  сглаживание  изображения  без  шума.  В  случае  добавления  шума,  после  сглаживания,  качество  изображения  может  быть  хуже,  чем  качество  изображения,  полученного  с  использованием  моделей,  устраняющих  шум,  например,  модель  ROF  [3].

Список  литературы:

1.Сглаживание  цифровых  сигналов.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://habrahabr.ru/post/184728/.  Дата  обращения:  9.11.2014.

2.Chan  T.F.,  Shen  J.  Image  processing  and  analysis:  Variational,  PDE,  Wavelet,  and  stochastic  methods.  SIAM,  2005.  —  400  p.

3.Rudin  L.I.,  Osher  S.,  Fatemi  E.  Nonlinear  total  variation  based  noise  removal  algorithms//Physica  D.  —  1992.  —  Vol.  60.  —  P.  259—268.