Статья опубликована в рамках: XXIX Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 01 апреля 2015 г.)
Наука: Информационные технологии
Секция: Теоретические основы информатики
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МОДЕЛЬ СОГЛАСОВАНИЯ РЕПЛИК В КОНЕЧНОМ СЧЕТЕ В БАЗАХ ДАННЫХ NOSQL
Цвященко Евгений Васильевич
аспирант Московский государственный технический университет им. Н.Э. Баумана, РФ, г. Москва
E -mail: eugene.tsviashchenko@gmail.com
MODEL OF REPLICAS AGREEMENT EVENTUALLY IN NOSQL
DATABASES
Tsviashchenko Evgeny
postgraduate student Bauman Moscow state technical university, Russia, Moscow
АННОТАЦИЯ
В статье представлена модель согласования реплик в конечном счете в базах данных NoSQL. Получена оценка вероятности того, что в процессе обновления N реплик поступит хотя бы одно требование на чтение из необновленных реплик. При этом учитывался синхронный а асинхронный способы распространения изменений. Проведен натурный эксперимент в кластере до 25 узлов для доказательства адекватности модели.
ABSTRACT
In this paper the model of replicas agreement eventually in NoSQL databases was described. The estimate of probability that in the process of updating N replicas arrive at least one requirement to read from the unpatched replicas was obtained. This takes into account both synchronous and asynchronous methods of distribution changes. The nature experiment was made on up to 25 nodes cluster in order to proof model adequacy.
Ключевые слова: база данных NoSQL; согласованность в конечном счете; преобразование Лапласа-Стилтьеса; производящая функция, вероятность доступа; адекватность.
Keywords: NoSQL database; eventually consistency; Laplas-Stiltes transformation; generating function; access probability; adequacy.
Современные распределенные хранилища данных должны быть масштабируемыми, доступными и быстрыми. Эти системы, как правило, распределяют данные между различными машинами (и часто через центры обработки данных) по двум причинам: во-первых, для обеспечения высокой доступности в случае отказа компонентов и, во-вторых, чтобы обеспечить высокую производительность обработки запросов на нескольких репликах. Такие системы баз данных, построенные на парадигме распределенных хранилищ «ключ/значение», получили название NoSQL (Not-Only-SQL) [1]. Основными преимуществами этих систем являются: высокая масштабируемость (Hadoop — 4000 узлов, Riak — 6000 узлов), большое число реплик, а, следовательно, высокая надежность.
В базах данных NoSQL не поддерживается режим ведения транзакций, поэтому возникает проблема согласования данных. Поддержание требуемого уровня согласованности для каждой конкретной предметной области может регулироваться параметрами (N, W, R) [2]. Согласованность в конечном счете существенно уменьшает время реакции системы, но в таких системах всегда присутствует определенная вероятность доступа к рассогласованным данным, т. к. реплики будут согласованы только через некоторое время распространения обновлений.
Задача состоит в том, чтобы оценить вероятность, что в процессе обновления N реплик поступит хотя бы одно требование на чтение из необновленных реплик. Необходимо учитывать синхронный и асинхронный способы распространения изменений. Также, нужно доказать адекватность модели, проведя соответствующие натурные эксперименты.
На рис. 1 графически показаны варианты распространения изменений в базах данных NoSQL: синхронный режим (рис. 1а) и асинхронный режим (рис. 1б).
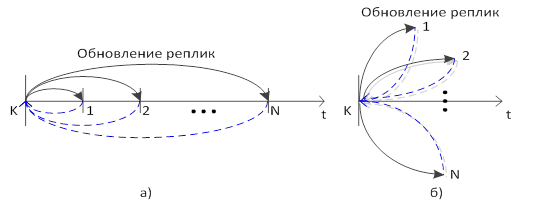
Рисунок. 1. Варианты распространения изменений: а) синхронный режим; б) асинхронный режим
Рассмотрим синхронный режим. В работе [3] разработана модель согласования реплик в конечном счете для случая синхронного режима распространения изменений (W=R=1). Для этого режима была получена вероятность P, что в процессе обновления N реплик поступит хотя бы одно требования на чтение из необновленных реплик:
|
|
(1) |
|
|
(2) |
где N+1 — общее число реплик для обновляемой записи (начальное изменение записи выполняется на (N+1)-ой реплике), λ — интенсивность чтения (пуассоновский входящий поток) записи из каждой реплики (1…N), на которую распространяется обновление, Ψi+1(s) — преобразование Лапласа-Стилтьеса (ПЛС) функции распределения вероятностей времени обновления (i+1)-ой реплики [3]. Для получения ПЛС Ψi+1(s) процесс обновления реплик был разделен на две составляющие: сетевую (передача данных по сети) и локальную (обновление структур памяти и файлового хранилища).
Рассмотрим асинхронный режим. В работе [4] разработана модель согласования реплик в конечном счете для случая асинхронного режима распространения изменений (W=R=1). Для этого режима была получена следующая оценка вероятности H, что в процессе асинхронного обновления N реплик поступит хотя бы одно требование на чтение из необновленных реплик:
|
|
(3) |
где Λi(s) — ПЛС сетевой составляющей времени обновления i-ой реплики, полученное в [3].
Модельные эксперименты показали, что при малых N (порядка 3) и незагруженной высокоскоростной сети передачи данных (1 Гбит/с) система NoSQL позволяет обеспечить свойство согласованности по чтению на уровне 0,99 (двух девяток) при синхронном режиме распространения изменений, и на уровне трех девяток при асинхронном режиме.
Для доказательства адекватности модели был проведен натурный эксперимент на кластере Riak [5] размером до 25 виртуальных узлов. Для проведения испытаний были арендованы виртуальные узлы, предоставленные компанией Digital Ocean [6]. Из описания процесса обновления реплик в системе NoSQL Riak [5] можно сделать вывод о синхронном характере распространения изменений. При инициализации узла доступно несколько опций, среди которых можно выделить опцию private networking. При включении данной опции все узлы, арендованные пользователем, гарантированно находятся в одном центре обработки данных (ЦОД), что означает отсутствие подкластеров сети. Использовалась операционная система Ubuntu Server 14.04 [7], предустановленная поставщиком. Для выполнения последовательного чтения и записи были разработаны соответствующие прикладные программы. Riak предоставляет библиотеки для доступа к системе на следующих языках: Java, Erlang, Pyton, Ruby, из которых была выбрана библиотека Java. Java-приложения транслируются в промежуточный байт-код, который исполняется на любой виртуальной машине. Все процессы чтения и записи выполнялись непосредственно на узлах.
Основываясь на теореме Ляпунова [8], было получено минимальное число итераций, необходимое для достижения требуемой точности оценки вероятности при надёжности 0,95. Число итераций составило 4000. От эксперимента к эксперименту менялась интенсивность поступления требований на чтение и количество узлов N. Всего было проведено две серии экспериментов по 16 испытаний в каждой. Значения некоторых параметров модели такие, как интенсивность передачи данных внутри сегмента сети, интенсивность чтения данных из оперативной памяти и др., сложно оценить до проведения испытаний. Это связано с тем, что один физический узел объединяет несколько виртуальных узлов, с которыми работают много пользователей, что свидетельствует о наличии фоновой загрузки ресурсов. Для оценки неизвестных параметров модели часть экспериментальных данных использовалась для решения вариационной задачи методом наискорейшего спуска [9].
В табл. 1 представлены результаты натурных и модельных экспериментов, позволяющие судить об адекватности разработанной модели согласования реплик в конечном счете в базах данных NoSQL. Анализировались те экспериментальные значения, которые не использовались при адаптации модели.
Таблица 1.
Анализ адекватности модели
|
N |
λ (1/с) |
Вероятность P (см. (1)) |
Относительная погрешность |
|
|
Эксперимент |
Модель |
|||
|
3 |
15 |
0.03900 |
0.04494 |
0.13227 |
|
20 |
0.06450 |
0.05947 |
0.07794 |
|
|
8 |
15 |
0.22325 |
0.24112 |
0.07413 |
|
20 |
0.32400 |
0.30780 |
0.04998 |
|
|
16 |
5 |
0.32475 |
0.29351 |
0.09619 |
|
10 |
0.53850 |
0.50087 |
0.06987 |
|
|
24 |
5 |
0.37450 |
0.53533 |
0.30044 |
|
7 |
0.47050 |
0.65802 |
0.28498 |
|
|
4 |
16 |
0.11750 |
0.13461 |
0.12712 |
|
20 |
0.15500 |
0.16533 |
0.06249 |
|
|
24 |
0.18470 |
0.19496 |
0.05263 |
|
|
28 |
0.22100 |
0.22354 |
0.01136 |
|
|
6 |
7 |
0.12975 |
0.12439 |
0.04134 |
|
12 |
0.20325 |
0.20364 |
0.00193 |
|
|
17 |
0.27350 |
0.27573 |
0.00807 |
|
|
22 |
0.35750 |
0.34128 |
0.04536 |
|
Средняя относительная погрешность по двум сериям экспериментов составила 9 %. Из табл. 1 видно, что погрешность увеличивается с ростом N. Это можно объяснить увеличением влияния фоновой нагрузки. В реальной ситуации значение N редко устанавливают выше 10, поэтому большая погрешность при N=24 не является критичной.
Список литературы:
1.NoSQL. [Электронный ресурс]. — Режим доступа. — URL: http://ru.wikipedia.org/wiki/NoSQL (дата обращения 22.03.2015).
2.Редмон Э., Уилсон Д.Р. Семь баз данных за семь недель. Введение в современные базы данных и идеологию NoSQL. М.: ДМК Пресс, 2013. — 384 с.
3.Григорьев Ю.А. Цвященко Е.В. Анализ характеристик согласования реплик в конечном счете в базах данных NoSQL // Информатика и системы управления. — 2014. — № 3. — С. 3—11.
4.Григорьев Ю.А. Цвященко Е.В. Сильная и слабая согласованность в базах данных NoSQL // Информатика и системы управления. — 2014. — № 4. — С. 14—23.
5.Riak documentation. [Электронный ресурс]. — Режим доступа. — URL: http://docs.basho.com/index.html (дата обращения 22.03.2015).
6.Digital Ocean. [Электронный ресурс] — Режим доступа. — URL: https://www.digitalocean.com (дата обращения 22.03.2015).
7.Ubuntu OS 14.04. [Электронный ресурс] — Режим доступа. — URL: http://releases.ubuntu.com/14.04 (дата обращения 22.03.2015).
8.Теорма Ляпунова. [Электронный ресурс] — Режим доступа. — URL: https://ru.wikipedia.org/wiki/Теорема_Ляпунова (дата обращения 22.03.2015).
9.Метод наименьших квадратов. [Электронный ресурс] — Режим доступа. — URL: https://ru.wikipedia.org/wiki/Метод_наименьших_квадратов (дата обращения 09.03.2015).+
дипломов


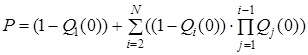 ,
, 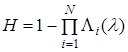 ,
,
Оставить комментарий