ВРЕМЯ  ГЛОНАСС:  ВЕЙВЛЕТ-АНАЛИЗ  ДАННЫХ  С1

Курбасова  Галина  Сергеевна

канд.  физ.-мат.  наук,  ведущий  научный  сотрудник  Крымской  астрофизической  обсерватории,  РФ,  п.  Научный,  Крым

E -mail:  gskurb@gmail.com

Вольвач  Александр  Евгеньевич

д-р  физ.-мат.  наук,  зам.  директора  по  науке  Крымской  астрофизической  обсерватории,  РФ,  п.  Научный,  Крым

E-mail:  

GLONASS  TIME:  WAVELET-ANALYSIS  C1

Kurbasova  Galina

candidate  of  Sciences,  Leading  Researcher  Crimean  Astrophysical  Observatory,  Russia,  Science,  Crimea

Vol'vach  Alexander

Dr.  of  Sciences,  Deputy  Director  for  Science  Crimean  Astrophysical  Observatory,  Russia,  Science,  Crimea

АННОТАЦИЯ

Глобальная  навигационная  спутниковая  система  ГЛОНАСС  обеспечивает  определение  точного  местоположения  и  времени  в  любой  точке  мира.  Высокоточная  система  оценки  разницы  во  времени  может  обеспечить  сантиметровую  точность  определения  местоположения.  Цель  этой  работы  заключается  в  изучении  структуры  данных  ГЛОНАСС  —  время  за  период  с  2009  по  2013  год  методом  вейвлет-анализа.

ABSTRACT

Global  navigation  satellite  system  GLONASS  provides  a  definition  of  the  exact  location  and  time  anywhere  in  the  world.  High-precision  evaluation  system  time  difference  can  provide  centimeter  accuracy  positioning.  The  aim  of  this  work  is  to  study  the  structure  of  the  GLONASS  time  data  for  the  period  from  2009  to  2013  using  wavelet  analysis.

Ключевые  слова:  ГЛОНАСС;  время;  вейвлет-анализ.

Keywords:   GLONASS;  time;  wavelet  analysis. 

Введение.   Российская  навигационная  система  ГЛОНАСС  —  Глобальная  Навигационная  Спутниковая  Система  (GNSS,  Global  Navigation  Satellites  System),  как  и  все  навигационные  спутниковые  системы,  предназначена  для  определения  местоположения,  скорости  движения,  а  также  точного  времени  морских,  воздушных,  сухопутных  и  других  видов  потребителей.  Общий  состав  системы  состоит  из  подсистемы  космических  аппаратов,  подсистемы  контроля  и  управления,  навигационной  аппаратуры  потребителей.  Спутники  системы  вращаются  в  своих  орбитальных  плоскостях  на  неизменной  средневысотной  орбите,  на  постоянном  расстоянии  от  поверхности  Земли.  Для  получения  сигнала  в  любое  время,  в  любой  точке  земного  шара  и  в  100  километрах  от  поверхности  земли  требуется  24  спутника.  Орбиты  этих  спутников  образуют  «сетку»  над  поверхностью  земли,  благодаря  чему  над  горизонтом  всегда  гарантированно  находятся  минимум  четыре  спутника,  а  созвездие  построено  так,  что,  как  правило,  одновременно  доступно  не  менее  шести.  На  борту  каждого  спутника  располагаются  несколько  эталонов  времени  и  частоты,  «высокоточные  атомные  часы».  Работает  всегда  один  эталон,  а  располагается  их  в  спутнике  несколько  (от  трёх  до  четырёх).  Задачи,  возложенные  на  систему  ГЛОНАСС,  включают:  1)  создание  (задание)  общеземной  геодезической  и  геоцентрической  систем  координат;  2)  распространение  единой  глобальной  высокоточной  шкалы  времени;  3)  создание  общеземной  сети  слежения  за  современными  движениями  земной  коры;  4)  координатно-временное  обеспечение  операций  в  космическом  пространстве  (международной  службы  вращения  Земли,  процесса  дистанционного  зондирования  Земли,  осуществляемого  в  интересах  картографирования  планеты,  мониторинга  экологического  состояния  её  поверхности  и  атмосферы;  работ,  реализуемых  методом  спутниковой  альтиметрии  с  целью  слежения  за  уровнем  мирового  океана,  изучения  его  физической  поверхности,  в  частности,  морской  топографической  поверхности  и  её  отличий  от  поверхности  геоида  (квазигеоида),  а  также  изучения  закономерностей  глобальной  циркуляции  водных  масс).

В  системе  ГЛОНАСС  используются  навигационные  космические  аппараты,  вращающиеся  по  круговой  геостационарной  орбите  на  высоте  ~  19100  км.  Период  обращения  спутника  вокруг  Земли  равен  в  среднем  11  часам  45  минутам.  Время  эксплуатации  спутника  —  5  лет;  за  этот  период  параметры  орбиты  спутника  не  должны  отличаться  от  номинальных  значений  более  чем  на  5  %.

Система  ГЛОНАСС  является  без  запросной,  поэтому  количество  потребителей  системы  не  ограничено.  Помимо  основной  функции  —  навигационных  определений,  —  система  позволяет  производить  высокоточную  взаимную  синхронизацию  стандартов  частоты  и  времени  на  удалённых  наземных  объектах  и  взаимную  геодезическую  привязку. 

ГЛОНАСС-время:  исходные  данные.  Все  спутники  ГЛОНАСС  оснащены  светоотражателями  для  их  лазерной  локации.  ГЛОНАСС-спутники  распространяют  общую  временную  шкалу,  определенную  как  ГЛОНАСС-время.  ГЛОНАСС-время  с  1  января  1999  г.  имеет  постоянный  сдвиг  по  шкале  международного  атомного  времени  (TAI,  International  Atomic  Time)  на  32  с.  Соотношение  между  ГЛОНАСС-время  и  Всемирным  координированным  временем  (UTC,  Coordinated  Universal  Time)  имеет  вид:  [UTC-  ГЛОНАСС-время]  =  0с+  C1,  где  временная  разница  0с  постоянна,  а  значения  временной  последовательности  (сигнала)  С1  меняются  со  временем  (порядка  нескольких  сотен  наносекунд  с  момента  1977  июль).  Разница  между  ГЛОНАCC-время  и  TAI  включает  переменное  число  секунд:  с  момента  2009  Января  1,  0  +  ч  UTC  до  момента  2012  Июль  1,  0ч  UTC:

[TAI-ГЛОНАСС-время]  =  34c  +  C1; 

с  момента  2012  Июль  1,  0  год  UTC: 

[TAI-ГЛОНАСС-время]  =  35c  +  C1,  где  значения  С1  представлены  на  0ч  UTC  каждый  день.

Значения  С1  исчисляются  по  данным  наблюдений  ГЛОНАСС  в  астрогеодинамической  обсерватории  в  Боровце  (Польша),  Ежесуточные  значения  С1  публикуются  в  ежемесячных  циркуляр  Международного  бюро  весов  и  измерений  (BIPM,  Bureau  International  des  Poids  et  Mesures).  Информация  о  соотношении  шкал  времени  UTC  и  TAI  с  шкалами  ГЛОНАСС-время  предоставляется  в  годовых  отчетах  BIPM  [3].  В  годовых  отчётах  BIPM  с  2011  г.  также  публикуются  значение  С0’  и  С1’,  которые  относятся,  соответственно,  к  обработке  наблюдений  Глобальной  Системы  Позиционирования  (GPS,  Global  Positioning  System)  в  Морской  обсерватории  США  (USNO,  United  States  Naval  Observatory)  и  наблюдений  ГЛОНАСС  в  Институте  метрологии  времени  и  пространства  (ВНИИФТРИ)  России.  Cпутники  GPS  и  ГЛОНАСС  широко  используются,  в  частности,  BIPM  для  синхронизации  атомных  часов  различных  лабораторий  мира.  Точность  синхронизации  составляет  2  нс  для  расстояний  до  1000  км,  и  6  нс  —  более  1000  км  [4].

Вейвлет-анализ.   При  выборе  метода  анализа  сигнала  С1  нами  была  принята  во  внимание  неоднородность  сигнала  во  времени.  Традиционное  преобразования  Фурье,  основанное  на  том,  что  функция  преобразования  покрывает  всю  временную  ось,  не  дает  представления  о  локализации  процесса  во  времени  [1].  Наоборот,  функция  одномерного  вейвлет-преобразования  хорошо  локализована  и  во  времени,  и  по  частоте.  Для  решения  задачи  восстановления  сигнала  С1  и  анализа  составляющей  шума  нами  использовались  программы  пакетного  вейвлет-анализа  из  состава  программного  обеспечения  MATLAB(2008a)  [5].

На  рисунке  1  приведен  график  ежемесячных  стандартных  отклонений  значений  С1  за  период  2009—2013  год.

Рисунок  1.  Стандартные  отклонения  S 1:  ежемесячная  характеристика  дисперсии  отдельных  измерений

Для  построения  графика  использовались  данные  BIPM  [3].  Приведенный  на  рисунке  1  график  величин  S1  отражает  резкое  снижение  дисперсии  отдельных  измерений  с  2010  года.  Тем  не  менее,  максимальная  неопределённость  измерений  С1  на  интервале  2010—2013  год  составляет  100  нс  (рис.  2,  график  сигнала  С1). 

Сущность  вейвлет-анализа  состоит  в  преобразовании  частотно-временного  пространства  в  масштабно-временное  пространство:  чем  больше  масштаб  а,  тем  меньше  различимы  детали  сигнала  и  наоборот,  т.  е.  выбор  масштаба  обратно  пропорционален  частоте.  Для  перекрытия  локальной  функцией  ψ  вейвлета  всей  временной  оси  пространства  используется  операция  сдвига  (смещения  по  временной  оси):  ψ(b,  t)  =  ψ(t  –  b),  где  значение  b  для  непрерывного  вейвлет-преобразования  является  величиной  непрерывной.  Коэффициенты  вейвлет-преобразования  С(a,  b)  содержат  комбинированную  информацию  об  анализируемом  сигнале  и  об  используемом  вейвлете.

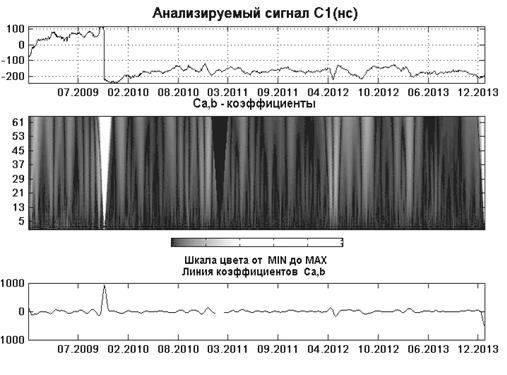
Рисунок  2.  Вейвлет-анализ  данных  С1  (соотношения  шкал  времени  UTC  и  TAI  со  шкалой  ГЛОНАСС).  Для  анализа  использовались  вейвлеты  Хаара

Поэтому  результаты  вейвлет-анализа  в  значительной  степени  зависят  от  выбора  порождающей  вейвлет  функции.  С  целью  обнаружения  локальных  особенностей  С1  нами  использовались  различные  типы  вейвлетов.  Наиболее  подходящими  для  поставленной  задачи  оказались  вейвлеты  Хаара  (непрерывное  вейвлет-преобразование)  и  вейвлеты  Добеши  (db2,  дискретное  вейвлет-преобразование). 

На  рисунке  2  пведены  графики:  исходных  данных  С1,  спектр  непрерывного  вейвлет-преобразования  С(a,  b)  ,  линии  коэффициентов. 

Спектр,  соответствующий  выбранному  вейвлет-базису,  в  отличие  от  спектра  Фурье,  является  двухмерным  и  определяет  двухмерную  поверхность  в  пространстве  переменных  a  и  b.

Чем  точнее  локальная  особенность  сигнала  совпадает  с  соответствующей  функцией  вейвлета,  тем  эффективнее  выделение  этой  особенности  на  соответствующей  масштабной  строке  вейвлетного  спектра.  Большие  значения  масштабов  соответствуют  расширениям  сигнала,  а  малые  значения  —  сжатиям.  График  С(а,b)  на  рисунке  2  показывает,  что  для  сильно  сжатого  вейвлета  Хаара  характерной,  хорошо  выделяемой,  локальной  особенностью  является  скачок  сигнала,  причем  выделяется  не  только  скачок  функции,  но  и  направление  скачка.  Так  как  непрерывное  преобразование  сигналов  содержит  очень  большой  объем  информации  [1],  то  разрыв  непрерывности  и  его  локализация  по  времени  в  анализируемом  сигнале  обнаруживается  с  высокой  точностью.  На  рисунке  2,  график  С(a,b)  эта  особенность  сигнала  выделяется  насыщенным  чёрным  цветом  и  разрывом  линии  коэффициентов. 

Для  полной  информации  о  структуре  анализируемого  сигнала  С1  нами  проведена  фильтрация  шума  и  последующий  анализ  составляющей  шума.

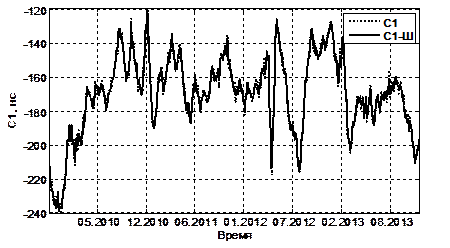
Рисунок  3.  Исходный  С1  и  отфильтрованный  от  шума  С1-  Ш  сигнал

Причём,  для  очистки  зашумлённого  сигнала  использовалось  дискретное  вейвлет-преобразование  сигнала  С1.  В  качестве  базовых  функций  выбраны  вейвлеты  из  семейства  Добеши.  Ранее  нами  было  установлено  преимущество  этих  вейвлетов  в  дискретном  вейвлет-анализе  наземных  и  космических  измерений  инсоляции  [2].  На  рисунке  3  приведены  графики  исходного  зашумленного  сигнала  (пунктирная  линия)  С1  и  отфильтрованного  от  шума  С1-  Ш  (сплошная  линия).

Рисунок  4.  Вейвлет-анализ  составляющей  шума  в  данных  С1:  а)  —  график  составляющей  шума;  б)  —  гистограмма  и  комулятивная  гистограмма;  в)  —  автокорреляции  и  FFT -спектр.

Вейвлет-анализ  составляющей  шума  в  сигнале  С1  (рис.  4)  показывает,  что  модель  шума  близка  к  стандартной  с  нулевым  средним  и  единичной  дисперсией.  Значения  описательных  статистик  равны:  среднее  0.0003  нс,  максимальные  отклонения  ±5  нс,  стандартное  отклонение  1.5  нс.

Выводы.  

1.  GPS  и  ГЛОНАСС  —  две  независимые  глобальные  навигационные  спутниковые  системы.  Каждая  обеспечивает,  независимо  друг  от  друга,  определения  точного  местоположения  и  времени  в  любой  точке  мира.  Смещение  времени  между  GPS  и  ГЛОНАСС  является  важным  параметром  в  комбинированной  обработке  GPS  /  ГЛОНАСС-измерений  [4].  Высокоточная  система  оценки  разницы  во  времени  может  обеспечить  сантиметровую  точность  определения  местоположения.  Спутники  ГЛОНАСС  широко  используются,  в  часности,  BIPM  для  синхронизации  атомных  часов  различных  лабораторий  мира.

2.  Непрерывное  вейвлет-преобразование  обнаруживает  наличие  и  локализацию  скачка  и  разрыва  в  последовательности  данных  С1.

3.  Вейвлет-анализ  составляющей  шума  в  сигнале  С1  (рис.  4)  показывает,  что  модель  шума  близка  к  стандартной  с  нулевым  средним  и  единичной  дисперсией.

4.  Несмотря  на  низкий  уровень  шума,  неопределённость  измерений  С1  на  интервале  2010  -2013год  остаётся  в  пределах  100нс.

Список  литературы:

1.Добеши  И.  Десять  лекций  по  вейвлетам.  Ижевск:  НИЦ  «Регулярная  и  хаотическая  динамика»,  2001,  —  464  с.

2.Курбасова  Г.С.,  Вольвач  O.Є.  Вейвлет-аналіз  наземних  і  космічних  вимірів  локальної  інсоляції.  //  Космічна  наука  і  технологія.  —  2014.  —  Т.  20.  —  №  4.  —  С.  42—49.

3.Annual  Report  BIPM  №№  5,  6,  7,  8,  9.  -2015.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.bipm.org

4.Daly  P.,  Kitchinc  I.D.,  Allan  D.W.,  Peppler  T.K.  Frequency  and  time  stability  of  GPS  and  GLONASS  clocks.  //  INTERNATIONAL  JOURNAL  OF  SATELLITE  COMMUNICATIONS.  —  1991.  —  Vol.  9.  —  P.  11—22 

5. For  use  with  MATLAB.  User’s  Guide  //  The  MathWorks,  Inc.  —  2002.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.mathworks.com