ТРАНСЗВУКОВОЕ  ОБТЕКАНИЕ  ПРОФИЛЯ  СТАБИЛИЗАТОРА  ПРИ  ОТКЛОНЕНИИ  РУЛЯ  ВЫСОТЫ

Бабарыкин  Константин  Валентинович

канд.  физ.-мат.  наук,  инженер,  Санкт-Петербургский  государственный  университет,  РФ,  г.  Санкт- Петербург

E-mail: 

TRANSONIC  FLOW  PAST  A  STABILIZER  AIRFOIL  WITH  A  DEFLECTED  ELEVATOR

Babarykin  Konstantin

candidate  of  Science,  engineer,  Saint-Petersburg  State  University,  Russia,  Saint-Petersburg

Работа  выполнена  при  поддержке  РФФИ  (проект  №  13-08-00288)

Исследования  проведены  с  использованием  вычислительных  ресурсов  Ресурсного  Центра  «Вычислительный  центр  СПбГУ»  ( http://cc.spbu.ru)

АННОТАЦИЯ

Проведено  численное  исследование  трансзвукового  обтекания  профиля  горизонтального  стабилизатора.  В  расчетах  использовалась  вычислительная  программа  Ansys-14  Fluent.  Осуществлены  расчеты  для  чисел  Маха  набегающего  потока,  больших  0,8.  Исследовано  влияние  отклонения  руля  высоты  на  подъемную  силу  профиля.  Показано  аномально  резкое  уменьшение  коэффициента  подъемной  силы  при  сравнительно  небольшом  отклонении  руля  высоты  для  числа  Маха  0,83.

ABSTRACT

A  numerical  investigation  of  transonic  flow  past  a  horizontal  stabilizer  airfoil  is  carried  out.  The  well-known  solver  Ansys-14  Fluent  is  used.  Computations  for  freestream  Mach  numbers  greater  then  0,8  are  fulfilled.  An  influence  of  the  elevator  deflection  on  lift  force  is  studied.  An  abnormally  abrupt  drop  of  the  lift  coefficient  with  a  relatively  small  deflection  of  the  elevator  for  the  freestream  Mach  number  of  0,83  is  shown.

Ключевые  слова:  трансзвуковое  течение;  профиль;  коэффициент  подъемной  силы;  руль  высоты; 

Keywords:   transonic  flow;  airfoil;  lift  coefficient;  elevator; 

Введение.  Постановка  задачи.

В  настоящей  работе  рассматривается  трансзвуковое  обтекание  профиля  горизонтального  стабилизатора.  Длина  профиля  равна  1  м,  максимальная  толщина  составляет  8,7  %  от  длины  хорды,  длина  руля  высоты  равна  37  %  длины  хорды.  Форма  профиля  представлена  на  рис.  1.

Рисунок  1.  Профиль  стабилизатора  с  отклонением  руля  высоты  5°

На  этом  рисунке  x,  y  —  отнесенные  к  длине  хорды  координаты,  θ  —  угол  отклонения  руля  высоты.  Форма  задается  выражениями 

y (x)  =  y_lths(x)  при  x  ≤  0,63

y (x)  =  y_lths(x)  +  (x  –  0,63)  tg  θ  при  0,63  ≤  x  ≤  1,

где  y_lths(x)  соответствует  известному  профилю  стабилизатора  LTHS.

Целью  настоящей  работы  является  изучение  картины  течения  около  профиля  и  его  характеристик  при  числах  Маха  набегающего  потока  M_∞  >  0,8,  когда  может  наблюдаться  формирование  нескольких  сверхзвуковых  зон  на  поверхности  профиля.  Их  слияние  или  расщепление  при  небольших  изменениях  условий  обтекания  может  приводить  к  резкому  изменению  коэффициента  подъемной  силы  C_L.  Ранее  в  [1—3]  изучалось  обтекание  аэродинамического  профиля  Whitcomb  при  отклонении  элерона  от  нейтрального  положения.  Было  обнаружено,  что  при  определенных  условиях  имеют  место  резкие  изменения  C_L  при  малом  изменении  геометрии.  Рассматриваемый  в  настоящей  работе  профиль  стабилизатора  также  имеет  управляющий  элемент  в  виде  руля  высоты,  что  обуславливает  возникновение  аналогичных  явлений  при  его  отклонении  от  нейтрального  положения. 

Проводились  расчеты  обтекания  профиля  равномерным,  со  слабой  турбулентностью,  потоком,  известной  программой  ANSYS  Fluent  14.  Параметры  набегающего  потока  соответствуют  условиям  атмосферы  на  высоте  10  км:  давление  p_∞  =  26434  Па,  температура  T_∞  =  223,15  K,  использовалась  модель  турбулентности  SST  k-ω  [4],  достаточно  хорошо  описывающая  течение  как  в  пограничном  слое,  так  и  в  области  свободного  потока. 

Расчетная  область  представляет  собой  круг  с  радиусом  99  длин  хорды.  Сетка  сгущена  в  небольшой  области  около  профиля  и  разрежена  в  направлении  внешних  границ  области  (рис.  2). 

Рисунок  2.  Схема  расчетной  области

Удаленность  внешней  границы  позволяет  ставить  на  ней  стандартное  для  Fluent  граничное  условие  дальнего  поля.  Такой  способ  построения  сетки  обеспечивает  достаточную  точность  решения,  и  с  другой  стороны,  позволяет  минимизировать  влияние  внешних  границ.  Немаловажно  и  то,  что  в  этом  случае  количество  элементов  получается  не  слишком  большим  (в  данном  случае  около  200  тыс.),  что  дает  возможность  избежать  больших  вычислительных  затрат. 

Результаты  расчетов.  Анализ  поведения  C_L  при  отклонении  руля  высоты.

Для  исследования  влияния  отклонения  руля  высоты  проведена  серия  расчетов  для  значений  θ  =  0;  1;  1,5;  2;  3;  4°  при  фиксированном  числе  Маха  набегающего  потока  M_∞  =  0,83,  нулевом  и  отрицательном  (α  =  -0,4°)  углах  атаки.  Результаты  расчетов  показывают  (рис.  3),  что  имеет  место  резкое  изменение  подъемной  силы  при  сравнительно  малом  изменении  θ.

Рисунок  3.  Зависимость  коэффициента  подъемной  силы  от  угла  отклонения  руля  высоты

Изменения  коэффициента  подъемной  силы  обусловлены  изменением  картины  обтекания  профиля.  Рассмотрим  ее  эволюцию,  наблюдающуюся  при  нулевом  угле  атаки  вследствие  увеличения  θ.  На  рис.  4а—4г  приведены  результаты  расчета  для  различных  значений  θ.  Особенностью  данного  профиля  является  наличие  на  нижней  стороне  довольно  протяженного  участка  с  небольшой  кривизной,  что  может  приводить  к  формированию  нескольких  сверхзвуковых  зон.  Как  можно  видеть  из  рис.  4а,  уже  в  случае  «чистого»  профиля  наблюдается  зарождение  двух  зон  —  одна  сразу  у  носика  профиля,  другая  в  средней  его  части.  При  постепенном  подъеме  руля  высоты  этот  процесс  усиливается.  Наблюдается  довольно  быстрый  рост  размеров  этих  зон  (рис.  4б  и  4в),  затем  происходит  их  слияние  в  одну  (рис.  4г).  Это  приводит  к  уменьшению  аэродинамической  силы,  действующей  на  нижнюю  поверхность.  Такая  бифуркация  течения  происходит  и  на  отрицательном  угле  атаке,  но  в  силу  более  интенсивного  роста  сверхзвуковых  зон  заметно  раньше,  при  θ  =  1,5°.

Рисунок  4а.  Поля  числа  Маха,  θ   =  0°.

Рисунок  4б.  Поля  числа  Маха,  θ   =  1,5°.

Рисунок  4в.  Поля  числа  Маха,  θ   =  2°.

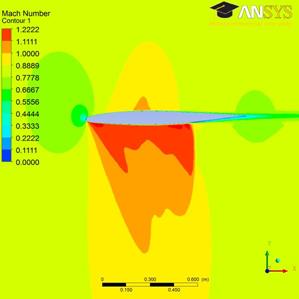
Рисунок  4г.  Поля  числа  Маха,  θ   =  3°.

На  верхней  части  профиля,  напротив,  наблюдается  резкое  уменьшение  размеров  местной  сверхзвуковой  зоны,  вызванное  торможением  потока  газа  перед  поднятым  рулем  (более  подробно  этот  процесс  рассмотрен  в  [1]  на  примере  профиля  с  элероном).  Таким  образом,  увеличивается  сила,  действующая  на  верхнюю  поверхность  профиля,  и  одновременно  уменьшается  сила,  действующая  на  нижнюю  поверхность.  Этим  и  объясняется  существенное  падение  коэффициента  подъемной  силы. 

Заключение

Осуществлено  численное  исследование  трансзвукового  обтекания  профиля  стабилизатора  программой  Fluent  с  использованием  модели  турбулентности  SST  k-ω.  Проведен  ряд  расчетов  на  различных  углах  атаки  при  отклонении  руля  высоты,  получены  зависимости  коэффициента  подъемной  силы  C_L  от  угла  отклонения.  Для  нулевого  угла  атаки  при  числе  Маха  набегающего  потока  M_∞  =  0,83  изучено  имеющее  место  существенное  изменение  C_L  при  сравнительно  небольшом  изменении  геометрии  профиля.

Список  литературы:

1.Бабарыкин  К.В.  Особенности  трансзвукового  обтекания  аэродинамического  профиля  при  отклонении  элерона  /  Естественные  и  математические  науки  в  современном  мире/  Сб.  ст.  по  материалам  XIII  междунар.  науч.-практ.  конф.  №  12  (12).  Новосибирск:  Изд.  «СибАК»,  2013.  —  С.  51—58. 

2.Kuzmin  A.,  Ryabinin  A.  Airfoils  admitting  anomalous  behavior  of  lift  coefficient  in  descending  transonic  flight  //  The  Seventh  Intern.  Conference  on  Comput.  Fluid  Dynamics.  —  2012  —  7  p.  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.iccfd.org/iccfd7/assets/pdf/papers/ICCFD7-4301_paper.pdf  (дата  обращения  29.10.2014).

3.Kuzmin  A.  Transonic  flow  past  a  Whitcomb  airfoil  with  a  deflected  aileron  //  International  Journal  of  Aeronautical  and  Space  Sciences  —  2013,  —  Vol.  14,  —  №  3.  —  pp.  210—214.

4.Menter  F.R.  Review  of  the  Shear-Stress  Transport  turbulence  model  experience  from  an  industrial  perspective  //  Intern.  J.  Comput.  Fluid  Dynamics,  —  2009,  —  vol.  23,  —  Issue  4.  —  pp.  305—316.