АЛГОРИТМ  ВЫБОРА  ЦЕНТРАЛЬНОГО  УЗЛА  В  ОДНОРАНГОВОЙ  СЕТИ  СО  СЛОЖНОЙ  СЛУЧАЙНОЙ  ТОПОЛОГИЕЙ

Власова  Анна  Михайловна

студент  Владимирского  государственного  университета  имени  А.Г.  и  Н.Г.  Столетовых,  РФ,  г.  Владимир

E -mail:  lost_anita@mail.ru

Голованов  Андрей  Евгеньевич

студент  Владимирского  государственного  университета  имени  А.Г.  и  Н.Г.  Столетовых,  РФ,  г.  Владимир

E-mail: 

Монахов  Юрий  Михайлович

канд.  техн.  наук,  доцент  кафедры  информатики  и  защиты  информации

Владимирского  государственного  университета  имени  А.Г.  и  Н.Г.  Столетовых,  РФ,  г.  Владимир

E-mail: 

" target="_blank">

CENTRAL  NODE  SELECTION  ALGORITHM  IN  AN  AD  HOC  NETWORK  WITH  COMPLEX  RANDOM  TOPOLOGY

Anna  Vlasova

student,  Vladimir  State  University,  Russia,  Vladimir

Andrey  Golovanov

student,  Vladimir  State  University,  Russia,  Vladimir

Yuri  Monakhov

PhD,  Associate  professor  of  Informatics  and  IT  Security  dept.,  Vladimir  State  University,  Russia,  Vladimir

АННОТАЦИЯ

Цель  исследования  —  разработать  способ  поиска  главного  узла,  который  с  низкой  степенью  вероятности  приведет  к  выбору  в  качестве  центра  принятия  решения  атакованного  и/или  захваченного  злоумышленником  узла.

В  процессе  работы  мы  разработали  алгоритм  для  поиска  центра  принятия  решений  (главного  узла  сети)  —  консенсусный  алгоритм  поиска  главного  узла,  основанный  на  рекомендациях.  Путем  моделирования  данного  алгоритма  мы  планируем  исследовать  его  сходимость  в  условиях  атак  и  децентрализованности  самого  процесса  голосования.

ABSTRACT

The  aim  of  the  research  is  to  devise  a  way  of  central  node  selection  which  will  show  low  probability  of  selecting  a  byzantine  node  as  a  decision-making  center.

During  our  research  we  have  developed  selection  algorithm  for  electing  the  node  that  will  perform  the  decision-making  —  consensual  recommendation-based  central  node  selection  algorithm.  By  implementing  these  algorithms  in  an  agent-based  model  we  are  planning  to  research  their  convergence  under  the  influence  of  attacks  and  decentralization  of  the  voting  processes.

Ключевые  слова :  сложные  сети;  случайная  топология;  кластеризация  сети;  оценка  уровня  доверия;  голосование;  выбор  главного  узла;  алгоритм  принятия  решения;  моделирование.

Keywords :  complex  networks;  random  topology;  network  clustering;  evaluation  of  trust;  election;  main  node  selection;  decision-making  algorithm;  modeling.

В  настоящее  время  широко  развиваются  и  распространяются  сети  со  сложной  топологией,  а  в  связи  с  ними  существует  и  продолжает  расширяться  спектр  атак  на  данный  вид  сетей.  Защита  таких  сетей  является  актуальной  проблемой,  так  как  узлы  в  таких  сетях,  как  правило,  имеют  небольшую  вычислительную  мощность  и  располагаются  в  незащищенных  местах,  а  доступ  к  ним  может  осуществляться  по  беспроводным  каналам.  Нарушение  работы  главного  узла  сети  (центра  принятия  решений)  приводит  к  наиболее  масштабным  последствиям  и  имеет  критическое  значение.  В  связи  с  этим  встает  вопрос  об  оптимальном  алгоритме  выбора  главного  узла  из  группы  идентичных,  а  анализ  различных  источников  показал,  что  в  настоящее  время  существует  много  научных  наработок  в  области  обеспечения  на  должном  уровне  безопасного  функционирования  сложных  сетей  и  предложения  для  них  специфичных  алгоритмов  в  условиях  атак  и  вторжений.  Данные  проблемы  рассматриваются  в  статьях  [1;  2;  3;  4].

Исходя  из  вышесказанного,  цель  исследования  определена  как  разработка  способа  поиска  главного  узла  в  сети,  который  с  низкой  степенью  вероятности  приведет  к  выбору  в  качестве  центра  принятия  решения  атакованного  и/или  захваченного  злоумышленником  узла. 

В  соответствии  с  целью  мы  определили  объект  и  предмет  исследования.  Предметом  исследования  является  процесс  голосования  в  одноранговой  сети,  направленный  на  выбор  главного  узла  из  числа  подобных  узлов  в  условиях  атак  или  уязвимостей,  а  объектом  исследования  являются  одноранговые  сети  со  сложной  случайной  топологией.

Прежде  чем  подробно  описать  сам  алгоритм,  необходимо  пару  слов  сказать  о  самой  модели  сети.  Мы  рассматриваем  статичную  сеть,  в  которой  присутствуют  области  повышенной  связности,  так  называемые  клики.  Под  кликой  будем  подразумевать  подраграфы,  вероятность  наличия  связей  между  двумя  соседними  вершинами  в  которых  близка  к  единице.

В  данной  работе  мы  учитываем,  что  захваченный  злоумышленником  узел  будет  проявлять  различного  рода  злонамеренную  активность  и  в  процессе  голосования:  будь  то  срыв  или  задержка  процесса  голосования,  распространения  ложной  информации  о  себе  и/или  о  соседних  узлах,  поэтому  для  процесса  голосования  принципиальное  значение  имеет  место  расположения  голосующего  узла. 

Мы  выделили  три  возможных  варианта  расположения  узла  в  сети:  в  клике  (рис.  1),  на  краю  клики  (рис.  2)  и  между  двумя  или  более  кликами  (рис.  3).  Узел,  расположенный  между  несколькими  кликами  условно  будем  называть  мостом.

Механизм  определения  типа  каждого  узла  сети  предлагаем  основывать  на  вычислении  кластерного  коэффициента  —  показателя  взаимосвязанности  соседей  узла  и  на  вычислении  собственной  центральности  узла,  которая  позволит  определить  степень  «важности»  узла,  т.  е.  количество  соседей  узла  и  связей  у  его  соседей.

Рисунок  1.  Атакованный  узел  в  клике

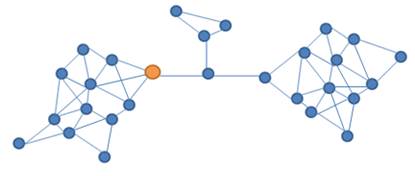
Рисунок  2.  Атакованный  узел  на  краю  клики

Рисунок  3.  Атакованный  узел  представляет  собой  место  соединения  нескольких  клик

Отношение  реального  количества  ребер,  которые  соединяют  ближайших  соседей  данного  узла  к  максимально  возможному  называется  коэффициентом  кластерности  узла.  Такое  определение  дает  Watts  и  Strogatz  в  работе  [5].  Формула  для  расчета  кластерного  коэффициента  может  быть  представлена  следующим  образом: 

С(i)  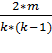=  ,                                            (1)

где:  k  —  число  ребер,  выходящий  из  узла  i;

m  —  число  ребер,  между  соседними  узлами  узла  i.

Определение  собственной  центральности  необходимо  также  и  для  того,  чтобы  можно  было  дать  приблизительную  оценку  времени  на  голосование  и  передачу  рекомендаций  каждым  узлом. 

Поскольку  каждый  из  узлов  в  сети  знает  топологию  только  в  рамках  своей  локальности,  поэтому  и  центральность  будем  вычислять  для  каждого  узла  только  с  учетом  его  соседних  узлов  и  их  непосредственных  соседей.  Известная  формула  2  дает  нам  следующее  соотношение:  умножение  матрицы  на  собственный  вектор  даёт  коллинеарный  вектор  —  тот  же  вектор,  умноженный  на  некоторое  скалярное  значение,  называемое  собственным  числом  матрицы. 

Ax  =  λx                                           (2),

где:  A  —  матрица  смежности  узла  с  его  соседями  и  соседями  соседей;

x  —  собственный  вектор  матрицы;

λ  —  собственное  значение  матрицы;

Из  2  получаем  формулу  3  для  собственного  центрального  значения  узла:

x_k  =                                              (3)

А  теперь  перейдем  непосредственно  к  консенсусному  рекомендательному  алгоритму  поиска  главного  узла.  Изначально  каждый  узел  в  сети  должен  самостоятельно  рассчитать  свой  кластерный  коэффициент  и  такой  параметр  как  собственная  центральность  узла. 

Перед  запуском  самого  процесса  голосования  каждый  узел  в  сети  получает  информацию  о  «локальности»,  т.  е.  информацию  о  соседях  и  соседях  своих  соседей,  содержащую  значение  их  кластерного  коэффициента  и  собственной  центральности.  После  происходит  обработка  полученных  сведений  каждым  узлом,  в  результате  которой  узел  получает  приближенную  оценку  топологии  области  вокруг  него  и  экзистенциально  принимает  решение  на  основе  величин  кластерных  коэффициентов  о  своем  месторасположении  (определяет  свой  тип). 

На  следующем  этапе  алгоритма  непосредственно  инициируем  процесс  голосования:  все  узлы  широковещательно  рассылают  всем  своим  соседям  информации  о  себе  (вектор  характеристик:  уровень  доверия  к  узлу,  количество  ресурсов  и  пр.)  как  о  кандидате  на  выдвижение  на  роль  главного  узла  в  сети.  В  данной  работе  мы  не  заостряем  внимание  на  перечислении  точного  перечня  используемых  характеристик.

Далее  в  зависимости  от  собственной  центральности  узла  ему  выделяется  определенное  время  на  обработку  сведений  о  кандидатах  из  числа  соседних  узлов,  которые  хранятся  на  узле  в  виде  очереди  с  приоритетом.  Каждый  узел  формирует  собственный  голос  за  наилучшего  кандидата  по  всему  вектору  полученных  характеристик.  Кластерный  коэффициент  и  величину  собственной  центральности  узла  необходимо  также  учитывать,  дабы  избежать  нелегитимного  завышения  своих  характеристик  каким-то  из  узлов,  т.  е.  мы  должны  учитывать  к  какому  из  трех  типов  узлов  относит  себя  наш  сосед  и  к  какому  типу  на  основе  кластерных  коэффициентов  его  соседей  относим  мы  его.

Стоит  отметить,  что  узел,  являющийся  мостом,  не  обрабатывает  списки  кандидатов,  а  лишь  передает  рекомендации  от  соседей  к  соседям,  для  того,  чтобы  отследить  загруженность  моста  и  определить  запускает  ли  данный  узел  механизм  фальсификации  голосования. 

По  истечению  выделенного  промежутка  времени  каждому  узлу  необходимо  удалить  всех  кандидатов  из  очереди,  за  исключением  лидирующего  кандидата,  находящего  соответственно  в  начале  очереди,  а  также  отправить  всем  своим  соседям  информацию  об  этом  кандидате,  дабы  не  давать  возможности  злоумышленнику  задерживать  процесс  голосования  сколь  угодно  долго,  т.  о.  на  всех  узла  происходит  асинхронная  передача  рекомендации  выбранного  кандидата  своим  соседям. 

Как  только  на  узел  поступают  новые  рекомендации  от  соседей,  он  снова  заносит  их  в  свою  очередь  с  приоритетом,  и  снова  ему  выделяется  лимит  времени  на  обработку  этих  данных.  Причем  узел  учитывает  лишь  характеристики  кандидатов,  а  не  количество  отданных  за  них  голосов  (количество  полученных  рекомендаций).  И  в  результате  новой  итерации  из  списка  удаляются  все  кандидаты,  кроме  лидера,  который  снова  рекомендуется  своим  соседям. 

Сбор,  обработку  и  передачу  рекомендаций  повторяют  до  тех  пор,  пока  не  будет  достигнут  консенсус  в  рамках  локальности,  т.  е.  не  будет  обновляться  список  кандидатов  на  каждом  узле  в  течение  длительного  времени.  Необходимое  количество  таких  итераций  может  быть  определено  в  ходе  эксперимента  поставленного  на  модели,  сходимость  данного  процесса  очевидно  будет  зависеть  от  размеров  клик  и  размера  самой  сети.  Вышеописанный  алгоритм  представлен  в  нотации  UML  в  виде  диаграммы  деятельности  на  рисунке  4.

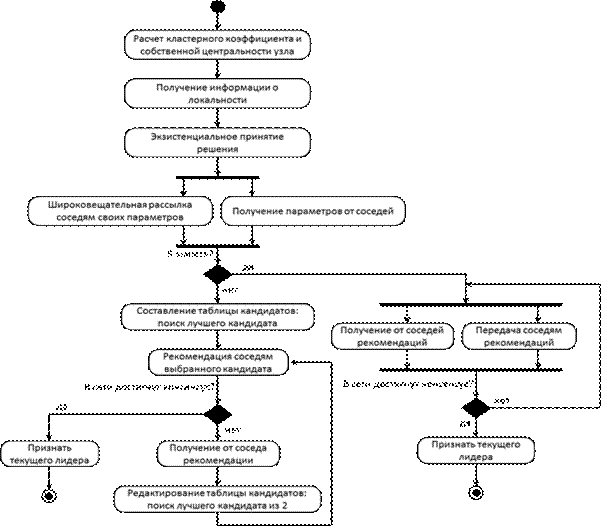
Рисунок  4.  Консенсусный  рекомендательный  алгоритм  поиска  главного  узла

На  сегодняшний  день  в  качестве  результатов  проведения  данного  научного  исследования  на  тему:  «Алгоритм  выбора  центрального  узла  в  одноранговой  сети  со  сложной  случайной  топологией»  выступает  разработанный  нами  алгоритма  голосования  для  поиска  центра  принятия  решений  —  «Консенсусный  алгоритм  поиска  главного  узла,  основанный  на  рекомендациях».

Тестирование  работы  данного  алгоритма  на  модели  позволит  выявить  необходимое  количество  туров  голосования  и  окончательного  принятия  решения  по  выбору  главного  узла,  а  также  это  даст  возможность  определить  достигается  ли  сходимость  данного  процесса  на  случайном  графе.  В  связи  с  этим  первостепенными  направления  нашего  дальнейшего  исследования  считаем:  разработку  модели  сложной  сети  и  моделирование  процесса  голосования,  в  последствии  ее  тестирование  на  случайном  графе  с  достаточно  большим  количеством  узлов  и  обработку  результатов  эмуляции  процессов  голосования.

Список  литературы:

1.Кривошеев  М.О.,  Ю.Н.  Логвинов  Протокол  консенсуса  в  асинхронных  сетях  с  неисправностями  //  Инженерный  вестник.  —  2013.  —  №  4.  [Электронный  ресурс]  —  Свободный  доступ.  —  URL:  http://www.ivdon.ru/magazine/archive/n4y2013/2154  (дата  обращения  14.07.14).

2.Ньюман  М.  Зарождающаяся  наука  о  сетях  //  Лекция  2009.  [Электронный  ресурс]  —  Свободный  доступ.  —  URL:  http://www.empatika.com/blog/santa-fe-newman-emerging-network-science  (дата  обращения  19.07.14).

3.Прогулова  Т.Б.  Топология  и  устойчивость  локально-мировых  сетей  //  Журнал  Международного  университета  природы,  общества  и  человека.  —  2009.  —  №  4.  [Электронный  ресурс]  —  Свободный  доступ.  —  URL:  http://www.swsys.ru/index.php?page=article&id=2369  (дата  обращения  21.07.14).

4.Maurer  A.,  S.  Tixeuil,  X.  Défago  Reliable  Communication  in  a  Dynamic  Network  in  the  Presence  of  Byzantine  Faults  //  Cornell  University  Library.  —  2014.  —  версия  2.  [Электронный  ресурс]  —  Свободный  доступ.  —  URL:  http://www.ivdon.ru/magazine/archive/n4y2013/2154  (дата  обращения  20.07.14).

5.Watts  D.J.,  Strogatz  S.H.  Collective  dynamics  of  “small-world”  networks.  //  Nature.  —  1998.  —  Vol.  393.  —  pp.  440—442.