МЕТОД  УСТРАНЕНИЯ  ШУМА  НА  MR-ИЗОБРАЖЕНИЯХ

Данг  Нгок  Хоанг  Тхань

аспирант  Тульского  государственного  университета,  РФ,  г.  Тула

E-mail: 

Фан  Зуй  Тунг

магистрант  Тульского  государственного  университета,  РФ,  г.  Тула

E-mail: 

A  METHOD  TO  REMOVE  NOISE  IN  MR-IMAGE

Dang  Ngoc  Hoang  Thanh

postgraduate  student  of  Tula  State  University,  Russia,  Tula

Phan  Duy  Tung

graduate  student  of  Tula  State  University,  Russia,  Tula

АННОТАЦИЯ

В  работе  предложен  метод  для  устранения  шума  на  MR-изображениях  [2;  3].  MRI-техника  (magnetic  resonance  imaging)  [2;  3]  используется  для  диагностики  болезни  с  помощью  изображений  в  медицине.  Такой  метод  построен  на  основе  модели  ROF  [4].

ABSTRACT

In  this  paper  we  propose  the  method  to  remove  noise  in  MR-image.  MRI  is  technique  for  disease  diagnostics  by  imaging.  This  method  based  on  ROF  model.

Ключевые  слова:  устранение  шума;  MR-изображение;  модель  ROF;  уравнение  Эйлера-Лагранжа. 

Keywords:  noise  removal;  MRI-image;  ROF  model;  equation  Euler-Lagrange. 

В  медицине  диагностика  болезни  с  помощью  изображений  достигла  больших  результатов.  В  том  числе  двумя  самыми  важными  техниками  являются  рентгеновские  снимки  и  MR-снимки.  Для  рентгеновской  техники  изображение  обычно  содержит  пуассоновский  шум,  а  для  MRI-техники  изображение  содержит  шум  Райса  (Rice,  Rician)  [3].  Устранение  шума  для  повышения  качества  изображений  в  этих  случаях  необходимо.

Устранение  шума  Райса  может  быть  выполнено  другими  техниками  [2;  3],  например,  вейвлет,  статистика  Байеса  и  т.  д.  В  этой  статье  мы  используем  вариационный  подход,  предлагаемый  Л.И.  Рудиным. 

В  пространстве    заданы  ограниченная  область    и  набор  .  Пусть    являются  гладкими  функциями  двух  переменных.  Задача  устранения  шума  можно  представить  в  виде: 

где:    —  функция  идеального  изображения, 

  —  функция  зашумлённого  изображения, 

  —  функция  шума.

Идеей  устранения  шума  на  изображении,  предлагаемым  Рудиным,  является  нахождение  функции  ,  выполняющей  следующее  условие  [4]:

где  .

Рассмотрим  шум  Райса.  Для  такого  типа  шума,  яркость  шума  в  каждой  точке  выполняет  распределение  Райса.  Т.  е.  для  каждого  события  :

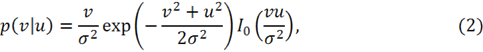
где:    —  стандартная  девиация  гауссовского  шума  в  вещественном  изображении  или  мнимом  изображении, 

  —  модифицированные  функции  Бесселя  первого  рода:

Мы  считаем,  что  интенсивность  зашумлённого  изображения  постоянна.  Т.  е.:

Согласно  (2),  имеем

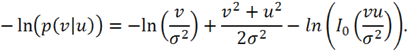
Поэтому  из  (3)  получим:

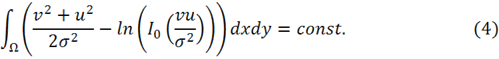
Задача  (1)  с  условием  (4)  может  быть  представлена  в  виде  следующей  задачи:

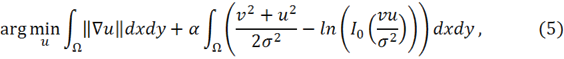
где    ненулевой  параметр.

Мы  можем  считать,  что  норма  в  (5)  является  нормой  в  пространстве  .  Это  значит,  что  .  Поэтому  (5)  переписывается  в  виде:

Алгоритм  решения

Для  решения  задачи  (6)  мы  используем  уравнение  Эйлера-Лагранжа  [1].  Положим: 

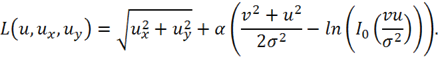
Тогда  уравнение  Эйлера-Лагранжа  задачи  (6)  имеет  вид:

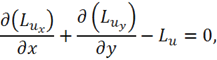
где    Поэтому  мы  получим  следующее  уравнение:

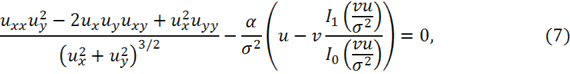
Для  решения  уравнения  (7)  мы  используем  метод  градиентного  спуска  с  шагом  времени  .  Выражение  для  нахождения    в  шаге    имеет  вид:

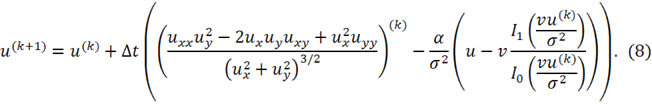
где 

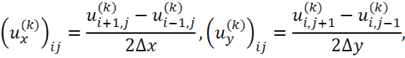
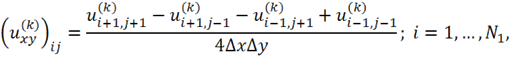
  —  число  точек  изображения  по  горизонтали,    —  число  точек  изображения  по  вертикали.

При  начальных  условиях:

Алгоритм  устранения  шума

Шаг  0.   Заданы    и  значение  .

Шаг  k.  

·     Вычислить    по  формуле  (8). 

·     Проверить  . 

·     Если  условие  выполнено,  стоп.  При  обратном  случае,  перейти  на  шаг  .

Экспериментальные  результаты 

В  эксперименте  мы  используем  изображение  черепа  человека  и  добавляем  шум  Райса  с  параметром  .  Для  оценки  качества  изображения  после  восстановления  мы  используем  критерий  PSNR  (peak  signal-to-noise  ratio,  пиковое  отношение  сигнала  к  шуму):

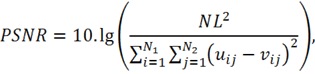
где:    —  размер  изображения, 

  —  интенсивность  яркости,  например,  для  восьмибитового  серого  изображения  . 

Чем  больше  PSNR,  тем  лучше  качество  изображения.  Функция  PSNR  не  ограничена. 

Значение  PSNR  восстановленного  изображения  больше,  чем  значение  PSNR  зашумленного  изображения.  Это  значит,  что  наш  метод  повышает  качество  изображения.

Рисунок  1.  Устранение  шума  на  изображении  черепа  человека

Заключение

В  этой  работе  предлагается  метод  устранения  шума  в  MR-изображениях.  Предлагаемый  метод  построен  с  помощью  модели  ROF.  Результат  устранения  шума  (значение  PSNR)  зависит  от  выбора  параметров    и  свойств  каждого  изображения.  Чем  больше  значение  яркости  точек  изображения,  тем  больше  шума  Райса  (т.  е.  шум  Райса  в  светлых  областях  изображения  больше,  чем  в  темных).  Поэтому  качество  восстановленного  изображения  ухудшается.

Список  литературы:

1.Gill  P.E.,  Murray  W.  Numerical  methods  for  constrained  optimization  Academic  Press  Inc.,  1974.  —  283  p.

2.Pierrick  C.,  Jose  V.M,  Elias  G.  et  al.  Robust  Rician  noise  estimation  for  MR  Image  //  Medical  image  analysis.  —  2010.  —  Vol.  14.  —  Is.  4  —  P.  483—493.

3.Robert  D.N.  Wavelet-based  Rician  noise  removal  for  Magnetic  resonance  imaging  //  Image  processing.  —  2002.  —  Vol.  8.  —  Is.  10.  —  P.  1408—1419.

4.Rudin  L.I.,  Osher  S.,  Fatemi  E.  Nonlinear  total  variation  based  noise  removal  algorithms  //  Physica  D.  —  1992.  —  Vol.  60.  —  P.  259—268.